python离群点检测_【Python算法】基于密度的离群点检测方法

1.平稳性检验

通过估计概率分布的参数来建立一个数据模型。如果一个数据对象不能很好地同该模型拟合，即如果它很可能不服从该分布，则它是一个离群点。

2.一元正态分布中的的离群点检测

正态分布是统计学中最常用的分布之一。 若随机变量x的密度函数如下式：

则称x服从正态分布，简称x服从正态分布N(μ,σ)，其中参数μ和σ分别为均值和标准差。

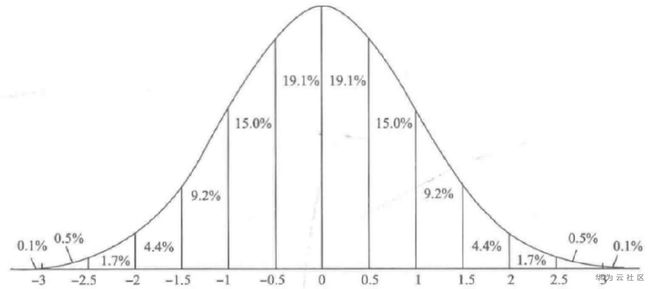
下图所示N(0,1)的密度函数：

N(0,1)的数据对象出现在该分布的两边尾部的机会很小，因此可以用它作为检测数据对象是否是离群点的基础。数据对象落在3倍标准差中心区域之外的概率仅有0.0027。

3.混合模型的离群点检测

混合模型是一种特殊的统计模型，它使用若干统计分布对数据建模。每一个分布对应一个簇，而每个分布的参数提供对应簇的描述，通常用中心和发散描述。

混合模型将数据看作从不同的概率分布得到的观测值的集合。概率分布可以是任何分布，但是通常是多元正态的，因为这种类型的分布不难理解，容易从数学上进行处理，并且已经证明在许多情况下都能产生好的结果。这种类型的分布可以对椭圆簇建模。

总的来说，混合模型数据产生过程为：定几个类型相同但参数不同的分布，随机地选取一个分布并由它产生一个对象。重复该过程m次，其中m是对象的个数。

具体地讲，假定有K个分布和m个对象X=x1,x2,…,xm。设第j个分布的参数为句，并设 A 是所有参数的集合，即A=a1, a2, … , ak。则$P(x_i|a_j)$是第i个对象来自第j个分布的概率。选取第j个分布产生一个对象的概率由权值$w_j(1 ≤ j ≤ K)$给定，其中权值（概率）受限于其和为1的约束，即：

于是，对象x的概率由以下公式给出：

如果对象以独立的方式产生，则整个对象集的概率是每个个体对象局的概率的乘积，公式如下：

对于混合模型，每个分布描述一个不同的组，即一个不同的簇。通过使用统计方法，可以由数据估计这些分布的参数，从而描述这些分布（簇）。也可以识别哪个对象属于哪个簇。然而，泪合模型只是给出具体对象属于特定簇的概率。

聚类时，混合模型方法假定数据来自混合概率分布，并且每个簇可以用这些分布之一识别。同样，对于离群点检测，用两个分布的混合模型建模，个分布为正常数据，而另一个为离群点。

聚类和离群点检测的目标都是估计分布的参数，以最大化数据的总似然。 离群点检测常用的简单的方法：先将所有数据对象放入正常数据集，这时离群点集为空集；再用一个迭代过程将数据对象从正常数据集转移到离群点集，该转移能提高数据的总似然。

具体操作如下：

假设数据集U包含来自两个概率分布的数据对象：M是大多数(正常)数据对象的分布，而 N 是离群点对象的分布。数据的总概率分布可以记作：$U(x) = (1 -\lambda M(x) + \lambda N(x)$，其中，x是一个数据对象；$\lambda ∈[0,1]$，给出离群点的期望比例。分布M由数据估计得到，而分布N通常取均匀分布。设Mt和Nt分别为时刻t正常数据和离群点对象的集合。初始t=0，M0=D，而N0≠Ø。

根据公式混合模型中公式$P(x|A)=\sum_{j=1}^K w_jP_j(x|a_j)$推导，在整个数据集的似然和对数似然可分别由下面两式给出：

其中PD、PMt、PNt分别是 、Mt、Nt的概率分布函数。

因为正常数据对象的数量比离群点对象的数量大很多，因此当一个数据对象移动到离群点集后，正常数据对象的分布变化不大。在这种情况下，每个正常数据对象的总似然的贡献保持不变。此外，如果假定离群点服从均匀分布，则移动到离群点集的每一个数据对象对离群点的似然贡献一个固定的量。这样，当一个数据对象移动到离群点集时，数据总似然的改变粗略地等于该数据对象在均匀分布下的概率（用λ加权）减去该数据对象在正常数据点的分布下的概率（用 l-λ加权)。从而，离群点由这样一些数据对象组成。这样，数据对象在均匀分布下的概率比正常数据对象分布下的概率高。

在某些情况下是很难建立模型的。例如，因为数据的统计分布未知或没有训练数据可用。在这种情况下，可以考虑其他不需要建立模型的检测方法。