python实现牛顿法_牛顿迭代法Python实现
例1:给定方程$$f(x) = x^2 + sin x - 1 = 0$$,判别该方程有几个实根,并用牛顿法求出方程所有实根,精确到$$10^{-4}$$.
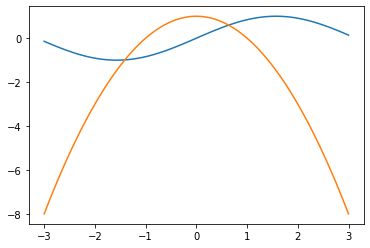
解:利用画图法观察根的所在区间为(-2,-1)和(0,1),其中蓝色为$$y=f(x)$$的曲线,橘黄色的直线是$$y=0$$.

画图代码:import numpy as np
import matplotlib.pyplot as plt
def fun(x):
return x**2 + np.sin(x) - 1
def plotCurves():
x = np.linspace(-3, 3, 100)
y = fun(x)
y1 = 0.*x
plt.plot(x,y)
plt.plot(x,y1)
def main():
plotCurves()
if __name__ == '__main__':
main()
另外一种观察方法是,将原来的函数分解为$$y=sin x$$和$$y=1-x^2$$两个函数,然后观察它们的交点,如下图所示:import numpy as np
import matplotlib.pyplot as plt
def plotCurves2():
x = np.linspace(-3, 3, 100)
y1 = np.sin(x)
y2 = 1 - x**2
plt.plot(x,y1)
plt.plot(x,y2)
def main():
plotCurves2()
if __name__ == '__main__':
main()
下面分别以-2和0为初值,用牛顿法求解根。由于$$f(x)=x^2 + sin(x) -1$$,因此$$f'(x) = 2 x + cos(x)$$.# -*- coding: utf-8 -*-
"""
给定方程f(x) = x^2 + sin x - 1 = 0,判别该方程有几个实根,并用牛顿法求出方程所有实根,精确到1e-4.
@author: morxio
"""
import numpy as np
def fun(x):
'''函数f(x)'''
return x**2 + np.sin(x) - 1
def dfun(x):
"""函数的导函数f'(x)"""
return 2 * x + np.cos(x)
def newton(x0, eps1, eps2, N):
"""
牛顿迭代法x = x - f(x)/f'(x)
x0:初值, N:最大迭代次数
eps1:根误差限,eps2:函数误差限
返回方程的根
"""
for k in range(0,N,1):
x = x0 - fun(x0) / dfun(x0)
print(x)
if np.abs(x) < 1:
if np.abs(x-x0) < eps1 or np.abs(fun(x)) < eps2:
print(f"经过{k:d}次迭代,初值为{x0:f}的根为{x:.6f}, 此时函数值为{fun(x):.6f}")
return (x,k, fun(x))
else:
if np.abs(x-x0)/np.abs(x) < eps1 or np.abs(fun(x)) < eps2:
print(f"经过{k:d}次迭代,初值为{x0:f}的根为{x:.6f}, 此时函数值为{fun(x):.6f}")
return (x,k, fun(x))
x0 = x
print(f"迭代超过{N:d}次,迭代失败")
def main():
newton(0.0, 1e-4, 1e-4, 1000)
newton(-2.0, 1e-4, 1e-4, 1000)
if __name__ == '__main__':
main()
结果:第0步: 相邻迭代步根误差为: 1.000000
第1步: 相邻迭代步根误差为: 0.331248
第2步: 相邻迭代步根误差为: 0.031684
第3步: 相邻迭代步根误差为: 0.000335
经过3次迭代,初值为0.637068的根为0.636733, 此时函数值为0.000000
第0步: 相邻迭代步根误差为: 0.473422
第1步: 相邻迭代步根误差为: 0.110144
第2步: 相邻迭代步根误差为: 0.006784
第3步: 相邻迭代步根误差为: 0.000026
经过3次迭代,初值为-1.409650的根为-1.409624, 此时函数值为0.000000
例2:构造计算$$\sqrt{C}, C>0$$的牛顿迭代公式,并计算$$\sqrt{115}$$的近似值,计算结果精确到$$10^{-5}$$.# -*- coding: utf-8 -*-
"""
构造计算sqrt{C}, C>0的牛顿迭代公式,并计算sqrt{115}的近似值,计算结果精确到1e-5.
@author: morxio
"""
import numpy as np
C = 115
x0 = 10
N = 1000
EPS = 1e-5
def fun(x):
'''函数f(x)'''
return x**2 - C
def dfun(x):
"""函数的导函数f'(x)"""
return 2 * x
def newton(x0, EPS, N):
"""
牛顿迭代法x = x - f(x)/f'(x)
x0:初值, N:最大迭代次数, eps:根误差限
"""
for k in range(0,N,1):
x = x0 - fun(x0) / dfun(x0)
print(x)
if np.abs(x) < 1:
if np.abs(x-x0) < EPS:
print(f"经过{k+1:d}次迭代,初值为{x0:f}的根为{x:.6f}, 此时函数值为{fun(x):.6f}")
return (x,k, fun(x))
else:
if np.abs(x-x0)/np.abs(x) < EPS:
print(f"经过{k+1:d}次迭代,初值为{x0:f}的根为{x:.6f}, 此时函数值为{fun(x):.6f}")
return (x,k, fun(x))
x0 = x
print(f"迭代超过{N:d}次,迭代失败")
def main():
newton(x0, EPS, N)
if __name__ == '__main__':
main()
结果:10.75
10.723837209302326
10.723805294811097
经过3次迭代,初值为10.723837的根为10.723805, 此时函数值为0.000000