python牛顿法与拟牛顿法_大白话介绍逻辑回归拟牛顿法+python实现
上一篇已经介绍过逻辑回归和牛顿法了,这篇就不重述了,直接介绍下拟牛顿法。
拟牛顿法的出现意义在于简化牛顿法的计算,主要在于通过迭代近似出牛顿法的分母海森矩阵,那么具体是如何迭代近似的呢?
经过k+1次迭代后的xk+1,将f(x)在xk+1处做泰勒展开有,取二阶近似有:
两边同时加一个梯度算子有:
整理得到:
![]()
令:
![]()
有:
![]()
这里我们对迭代过程中的海森矩阵做约束得到了拟牛顿的条件。
我们在迭代的时候可以先令初始化单位矩阵,下面附dfp迭代方法的步骤
根据这个步骤,下面是python源码,亲写亲测可运行:
#利用拟牛顿法求解逻辑回归,然后画图(详细版)
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
data=pd.read_csv("E:\\caffe\\study\\2_data.csv",sep=",")
#整理好数据
train_x=data.iloc[0:100,0:2]
train_y=data.iloc[0:100,2:3]
H=np.eye(3,3)
theta=np.mat([2,2,-10])#初始theta
eps=0.5
alpha=0.8
#定义函数
def h(theta,x):#LR假设函数
return(1.0/(1+np.exp(-1*(np.dot(theta,x)))))
def f(train_x,train_y,theta):#一阶导函数
a=np.mat([0,0,0])
# train_x=pd.concat([DataFrame([1 for i in range(len(train_x))]),train_x],1)
train_x["x3"]=[1.0 for i in range(len(train_x))]
for i in range(len(train_x)):
# a = a - (h(theta, np.mat(train_x.iloc[i, :]).T) - train_y.iloc[i, 0]) * np.mat(train_x.iloc[i, :])
a=a+ (h(theta,np.mat(train_x.iloc[i,:]).T)-train_y.iloc[i,0])*np.mat(train_x.iloc[i,:])
return a/len(train_x)
# return a
def d(train_x,train_y,theta,H):
ff=f(train_x,train_y,theta)
return np.dot(H,ff.T)*(-1)
def newtheta(train_x,train_y,theta,H,alpha):
dd=d(train_x,train_y,theta,H)
return theta+alpha*dd.T
def s(train_x,train_y,theta,H,alpha):
nt=newtheta(train_x,train_y,theta,H,alpha)
return nt-theta
def y(train_x,train_y,theta,nt):
nf=f(train_x,train_y,nt)
ff=f(train_x,train_y,theta)
return nf-ff
def newH(train_x,train_y,theta,H,alpha,nt):#修正H
ss=s(train_x,train_y,theta,H,alpha)
yy=y(train_x,train_y,theta,nt)
return (H+np.dot(np.dot(ss.T,ss),np.dot(ss.T,yy).I)-np.dot(np.dot(np.dot(np.dot(H, yy.T),yy),H),np.dot(np.dot(yy.T,yy),H).I))
def finaltheta(train_x,train_y,theta,H,alpha,eps):#迭代输出最后的theta
while (np.array(f(train_x,train_y,theta))[0][0]**2+np.array(f(train_x,train_y,theta))[0][1]**2+np.array(f(train_x,train_y,theta))[0][2]**2)**0.5>eps:
dd=d(train_x,train_y,theta,H)
nt=newtheta(train_x, train_y, theta, H, alpha)
ss=s(train_x,train_y,theta,H,alpha)
yy=y(train_x,train_y,theta,nt)
nH=newH(train_x,train_y,theta,H,alpha,nt)
theta=nt/abs(min(np.array(nt)[0]))
H=nH
else:
return theta
def pic(train_x,train_y,theta,H,alpha,eps):#画图
nt=finaltheta(train_x, train_y, theta, H, alpha, eps)
plot_x=[1,10]
plot_y=[((-1)*np.array(nt)[0][2]+(-1)*np.array(nt)[0][0]*plot_x[0])/np.array(nt)[0][1],((-1)*np.array(nt)[0][2]+(-1)*np.array(nt)[0][0]*plot_x[1])/np.array(nt)[0][1]]
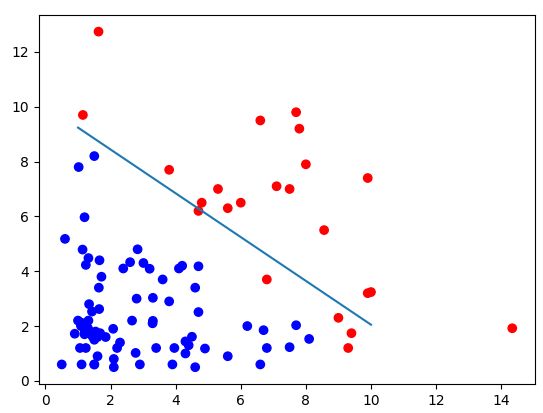
plt.scatter(train_x['x1'], train_x['x2'], c=["r" if i==1 else "b" for i in train_y["y"]])
plt.plot(plot_x, plot_y)
结果如图所示:
这里想说一下:
在实际调整代码的时候,发现,迭代效果会受到初始theta向量的影响,所以,如果自变量维度较少可以大致观察下可能的theta再初始化theta可能结果会比较好。
拟牛顿法当然也是要对于n为的自变量向量,theta一定要是n+1维的,这是不可以忽略的!