C++STL详解(七):stack、queue与priority_queue的使用及其模拟实现
文章目录
-
-
-
- stack
-
- stack的介绍
- 栈的使用
- queue
-
- queue的介绍
- 队列的使用
- priority_queue
-
- priority_queue的介绍
- 优先队列的使用
- 容器适配器
-
- 什么是容器适配器
- STL标准库中stack、queue和priority_queue的底层结构
- deque的简单介绍(了解)
- stack的模拟实现
- queue的模拟实现
- 仿函数
- priority_queue的模拟实现
-
- 向上调整算法
- 向下调整算法
- 代码实现
-
-
stack
stack的介绍
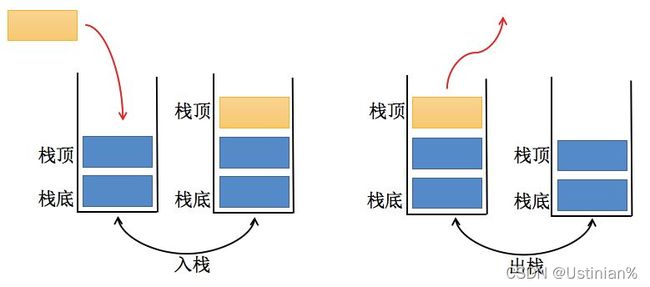
stack这种容器就像是手枪装填子弹然后开枪一样,先装进去的子弹会在下面然后是后打出来的,后装进去的子弹会在上面然后是先打出来的。
下面我们再来细说一下栈:
- stack是一种容器适配器,专门用在具有后进先出操作的上下文环境中,其删除只能从容器的一端进行元素的插入与提取操作。
- stack是作为容器适配器被实现的,容器适配器即是对特定类封装作为其底层的容器,并提供一组特定的成员函数来访问其元素,将特定类作为其底层的,元素特定容器的尾部(即栈顶)被压入和弹出。
- stack的底层容器可以是任何标准的容器类模板或者一些其他特定的容器类,这些容器类应该支持以下操作:
- empty:判空操作
- back:获取尾部元素操作
- push_back:尾部插入元素操作
- pop_back:尾部删除元素操作
- 标准容器vector、deque、list均符合这些需求,默认情况下,如果没有为stack指定特定的底层容器,默认情况下使用deque。
栈的使用
栈的函数接口:
| 函数说明 | 接口说明 |
|---|---|
| stack() | 构造空的栈 |
| empty() | 检测stack是否为空 |
| size() | 返回stack中元素的个数 |
| top() | 返回栈顶元素的引用 |
| push() | 将元素val压入stack中 |
| pop() | 将stack中顶部的元素弹出 |
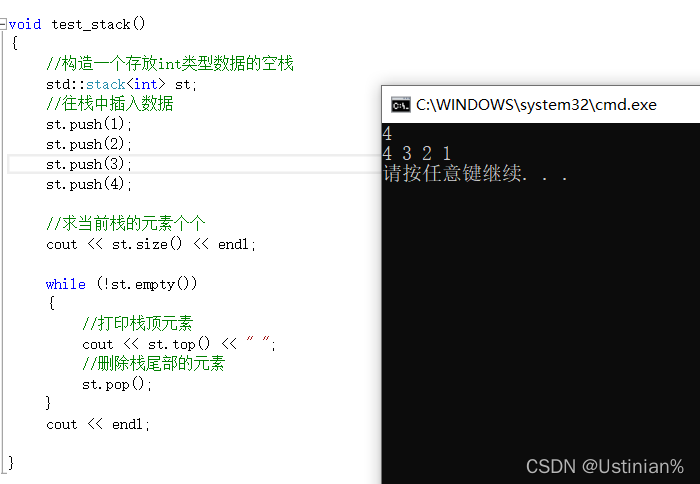
因为我们在前面学过string、vector与list了,那么现在对于这些函数的接口可以说已经是轻车熟路了,那么下面我们就来用一下吧。
void test_stack()
{
//构造一个存放int类型数据的空栈
std::stack<int> st;
//往栈中插入数据
st.push(1);
st.push(2);
st.push(3);
st.push(4);
//求当前栈的元素个数
cout << st.size() << endl;
while (!st.empty())
{
//打印栈顶元素
cout << st.top() << " ";
//将栈顶部的元素弹出
st.pop();
}
cout << endl;
}
queue
queue的介绍
下面我们来说一下队列:
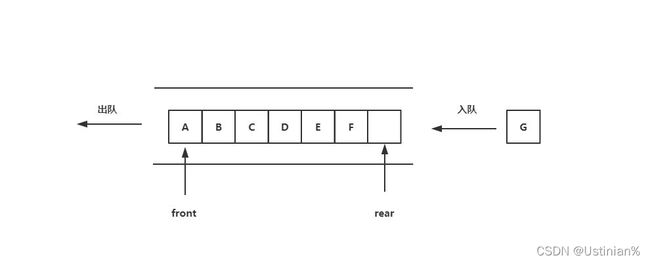
- 队列是一种容器适配器,专门用于在FIFO上下文(先进先出)中操作,其中从容器一端插入元素,另一端提取元素。
- 队列作为容器适配器实现,容器适配器即将特定容器类封装作为其底层容器类,queue提供一组特定的成员函数来访问其元素。元素从队尾入队列,从队头出队列。
- 底层容器可以是标准容器类模板之一,也可以是其他专门设计的容器类。该底层容器应至少支持以下操作:
- empty:检测队列是否为空
- size:返回队列中有效元素的个数
- front:返回队头元素的引用
- back:返回队尾元素的引用
- push_back:在队列尾部入队列
- pop_front:在队列头部出队列
- 标准容器类deque和list满足了这些要求。默认情况下,如果没有为queue实例化指定容器类,则使用标准容器deque。
队列的使用
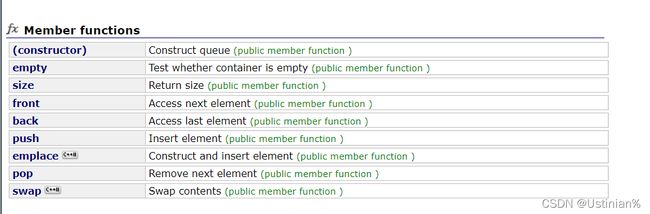
队列的函数接口:
| 函数声明 | 接口说明 |
|---|---|
| queue() | 构造空的队列 |
| empty() | 检测队列是否为空,是返回true,否则返回false |
| size() | 返回队列中有效元素的个数 |
| front() | 返回队头元素的引用 |
| back() | 返回队尾元素的引用 |
| push() | 在队尾将元素val入队列 |
| pop() | 将队头元素出队列 |
下面我们来使用一下队列的这些常用接口
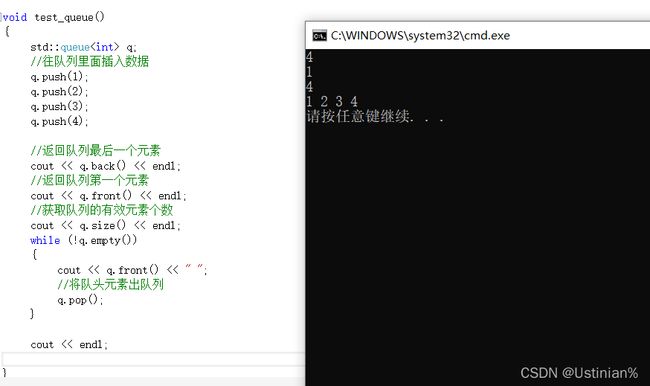
void test_queue()
{
std::queue<int> q;
//往队列里面插入数据
q.push(1);
q.push(2);
q.push(3);
q.push(4);
//返回队列最后一个元素
cout << q.back() << endl;
//返回队列第一个元素
cout << q.front() << endl;
//获取队列的有效元素个数
cout << q.size() << endl;
while (!q.empty())
{
cout << q.front() << " ";
//将队头元素出队列
q.pop();
}
cout << endl;
}
priority_queue
priority_queue的介绍
- 优先队列是一种容器适配器,根据严格的弱排序标准,它的第一个元素总是它所包含的元素中最大的。
- 优先队列与我们之前学的一个数据结构是比较类似的,那就是堆,且默认是我们的大堆。在堆中可以随时插入元素,并且只能检索最大堆元素(优先队列中位于顶部的元素)。
- 底层容器可以是任何标准容器类模板,也可以是其他特定设计的容器类。容器应该可以通过随机访问迭代器访问,并支持以下操作:
- empty():检测容器是否为空
- size():返回容器中有效元素个数
- front():返回容器中第一个元素的引用
- push_back():在容器尾部插入元素pop_back()
- :删除容器尾部元素
- 标准容器类vector和deque满足这些需求。默认情况下,如果没有为特定的priority_queue类实例化指定容器类,则使用vector。
优先队列的使用
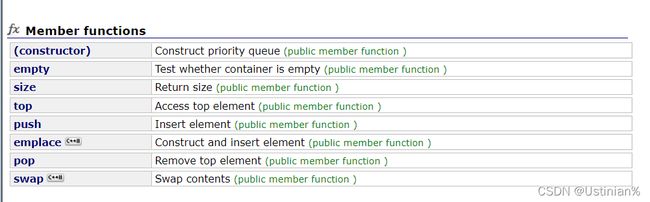
优先级队列的函数接口:
优先级队列默认使用vector作为其底层存储数据的容器,在vector上又使用了堆算法将vector中元素构造成堆的结构,因此priority_queue就是堆,所有需要用到堆的位置,都可以考虑使用priority_queue。注意:默认情况下priority_queue是大堆。
| 函数声明 | 接口说明 |
|---|---|
| priority_queue()/priority_queue(first, last) | 构造一个空的优先级队列 |
| empty( ) | 检测优先级队列是否为空,是返回true,否则返回false |
| top() | 返回优先级队列中最大(最小元素),即堆顶元素 |
| push(x) | 在优先级队列中插入元素x |
| pop() | 删除优先级队列中最大(最小)元素,即堆顶元素 |
下面我们来使用一下优先队列的常用接口吧
void test_priority_queue()
{
//默认是一个大堆,默认大的优先级高 less
std::priority_queue<int, std::vector<int>>pq;
//往优先队列里面插入数据
pq.push(3);
pq.push(5);
pq.push(6);
pq.push(1);
pq.push(4);
pq.push(2);
pq.push(10);
pq.push(3);
//判断优先队列是否为空
cout << pq.empty() << endl;
//返回优先队列中的有效元素个数
cout << pq.size() << endl;
while (!pq.empty())
{
//返回堆顶元素
cout << pq.top() << " ";
pq.pop();
}
cout << endl;
}
默认是大堆,如果想变成小堆的话,就写成下面这样:
//变成小堆,小堆的优先级高怎么处理 greater
std::priority_queue<int, std::vector<int>, std::greater<int>>pq;
但是需要我们包含一个头文件: #include
容器适配器
什么是容器适配器
适配器是一种设计模式(设计模式是一套被反复使用的、多数人知晓的、经过分类编目的、代码设计经验的总结),该种模式是将一个类的接口转换成客户希望的另外一个接口。
STL标准库中stack、queue和priority_queue的底层结构
虽然stack和queue中也可以存放元素,但在STL中并没有将其划分在容器的行列,而是将其称为容器适配器,这是因为stack和队列只是对其他容器的接口进行了包装(STL中stack和queue默认使用deque,而priority_queue则使用我们的vector)
deque的简单介绍(了解)
deque(双端队列):是一种双开口的"连续"空间的数据结构,双开口的含义是:可以在头尾两端进行插入和删除操作,且时间复杂度为O(1),与vector比较,头插效率高,不需要搬移元素;与list比较,空间利用率比较高。
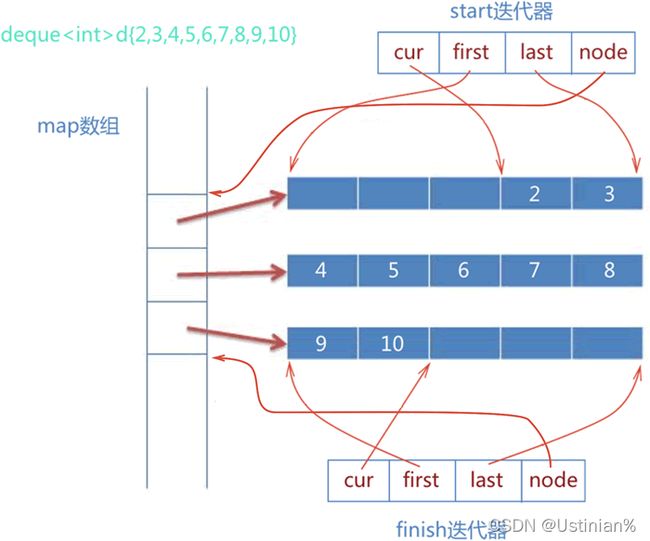
注意:deque并不是真正连续的空间,而是由一段段连续的小空间拼接而成的,实际deque类似于一个动态的二维数组,其底层结构如下图所示
双端队列底层是一段假象的连续空间,实际是分段连续的,为了维护其“整体连续”以及随机访问的假象,落在了deque的迭代器身上,因此deque的迭代器设计就比较复杂,如下图所示:
deque的优点:
- 与vector比较,deque的优势是:头部插入和删除时,不需要搬移元素,效率特别高,而且在扩容时,也不需要搬移大量的元素,因此其效率是必vector高的。
- 与list比较,其底层是连续空间,空间利用率比较高,不需要存储额外字段。
- deque在功能上可以说是vector与list的结合,但是并不能去替代二者,如果真的能替代两者我们就不用学vector和string了。
deque的缺点:
- deque有一个致命缺陷:不适合遍历,因为在遍历时,deque的迭代器要频繁的去检测其是否移动到某段小空间的边界,导致效率低下,而序列式场景中,可能需要经常遍历,因此在实际中,需要线性结构时,大多数情况下优先考虑vector和list,deque的应用并不多,而目前能看到的一个应用就是,STL用其作为stack和queue的底层数据结构。
stack的模拟实现
stack的模拟实现比较简单,通过容器适配器,复用其他容器的接口就可以直接实现
namespace mlf
{
//模拟实现栈
//容器适配器
//template>
//template>
template<class T, class Container = std::deque<T>>
class stack
{
public:
bool empty()
{
return _con.empty();
}
size_t size()
{
return _con.size();
}
T& top()
{
return _con.back();
}
void push(const T& x)
{
_con.push_back(x);
}
void pop()
{
_con.pop_back();
}
private:
Container _con;
};
}
queue的模拟实现
queue的模拟实现比较简单,通过容器适配器,复用其他容器的接口就可以直接实现
namespace mlf
{
template<class T, class Container = std::deque<T>>
//template>
class queue
{
public:
bool empty()
{
return _con.empty();
}
size_t size()
{
return _con.size();
}
T front()
{
return _con.front();
}
T back()
{
return _con.back();
}
void push(const T& x)
{
_con.push_back(x);
}
void pop()
{
_con.pop_front();
}
private:
Container _con;
};
}
仿函数
仿函数也称作仿函数类,本质是通过重载operator()实现的,使得该类的对象可以像函数一样去使用
为什么要使用仿函数呢?因为C语言中的函数指针用起来不太好用,因此在C++中,我们通过仿函数来代替它。
// 仿函数 -- 函数对象 这个类的对象可以像函数一样去使用
template<class T>
struct Less
{
bool operator()(const T& l,const T& r)
{
return l < r;
}
};
priority_queue的模拟实现
因为我们的优先级队列和我们的堆是类似的,既然和堆类似那么我们就不得不来说一下向上调整算法、向下调整算法。
向上调整算法
向上调整算法简单来说就是在一个大堆或者小堆中,我们尾插了一个数据,通过向上调整算法我们的堆依然是大堆或者小堆。
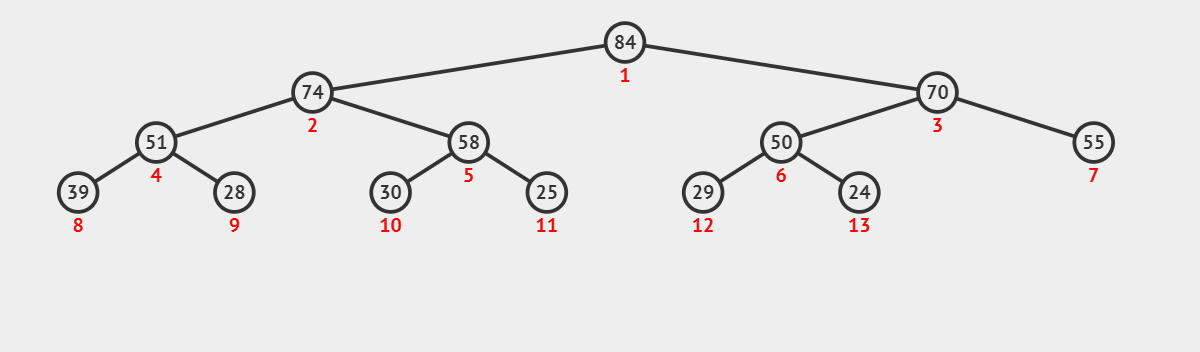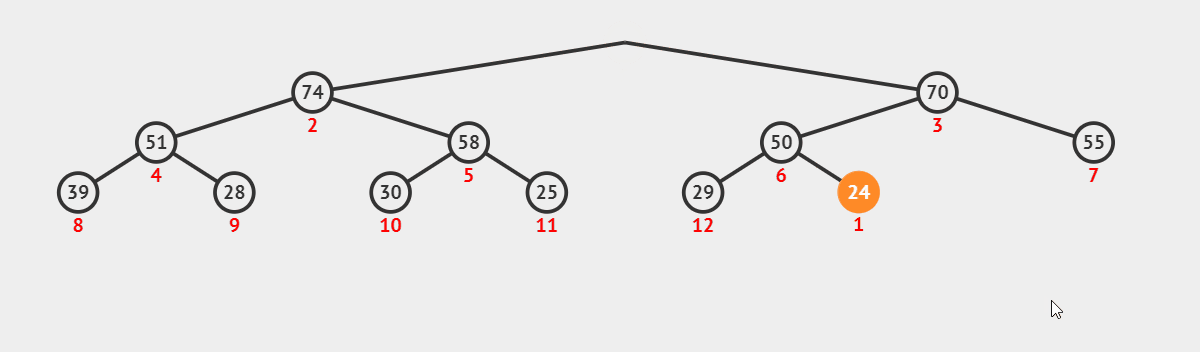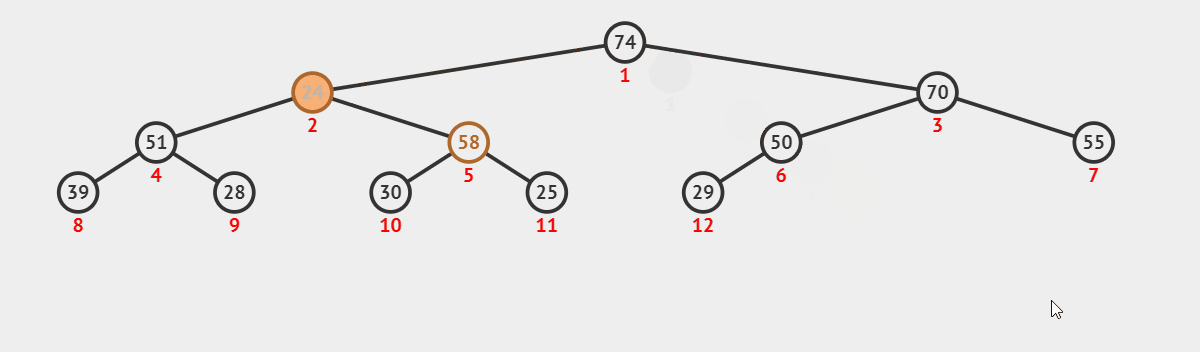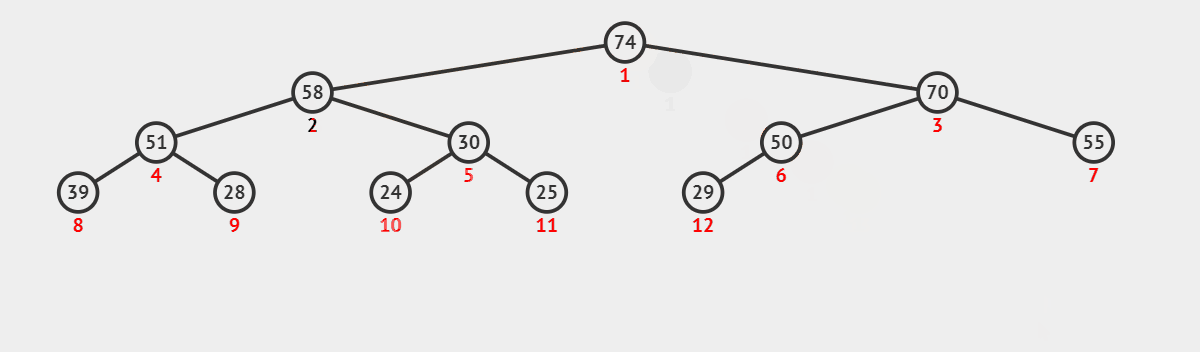
以大堆为例,我们通过动图来看一下向上调整算法
向上调整算法的思想:
- 当我们在堆中插入一个数据,我们将该节点与它的父亲节点进行比较
- 如果当前节点的值比父亲节点的值大,就交换两个节点的数据,并将父节点的下标赋给当前节点下标继续向上调整,如果当前节点的值比父亲节点的值小,就停止向上调整因为现在的堆已经是一个大堆了。
//向上调整法
void AdjustUp(size_t child)
{
//求出父节点的下标
size_t parent = (child - 1) / 2;
while (child > 0)
{
//父节点的值小于孩子结点的值
//就交换
if (_con[parent] < _con[child])
{
swap(_con[parent], _con[child]);
//更新父亲和孩子的下标
child = parent;
parent = (child - 1) / 2;
}
else
{
break;
}
}
}
向下调整算法
在一个大堆或者小堆中,我们想要删除堆顶的数据,但是我们不能够直接删除堆顶的数据,因此我们需要将堆顶数据与最后一个数据交换,然后删除掉最后一个数据(也就相当于删除掉了我们堆顶的数据)但是我们还想保持我们的大堆或者小堆,因此我们需要进行我们的向下调整算法将堆调整成大堆或者小堆。
以大堆为例,我们通过动图来看一下向上调整算法
向下调整算法的思想:
- 在未开始调整之前,我们是假定左孩子的值是大于右孩子的值的,因此我们需要将左孩子的值与右孩子的值进行比较一下,选出值较大的孩子
- 如果当前孩子的值是大于我们的父节点的值,那么我们就需要交换一下父节点与孩子节点的值,并将当前孩子节点的值作为新的父节点继续向下调整。反之则不需要向下调整,因为当前的堆已经是大堆了。
//向下调整法
void AdjustDown(size_t parent)
{
size_t child = parent * 2 + 1;
while (child < _con.size())
{
//我们这里是假定左孩子的值比较大
//因此我们需要将左孩子和右孩子的值比较一下
//更新一下
if (child + 1 < _con.size() && _con[child] < _con[child + 1])
{
child++;
}
//if (_con[parent] < _con[child])
if (com(_con[parent], _con[child]))
{
swap(_con[parent], _con[child]);
parent = child;
child = parent * 2 + 1;
}
else
{
break;
}
}
}
代码实现
namespace mlf
{
//仿函数
template<class T>
struct less
{
bool operator()(const T& l, const T& r)
{
return l < r;
}
};
template<class T>
struct greater
{
bool operator()(const T& l, const T& r)
{
return l > r;
}
};
template<class T, class Container = std::vector<T>,class compare = less<T>>
class priority_queue
{
public:
bool empty()
{
return _con.empty();
}
size_t size()
{
return _con.size();
}
T top()
{
return _con[0];
}
//向上调整法
void AdjustUp(size_t child)
{
compare com;
//求出父节点的下标
size_t parent = (child - 1) / 2;
while (child > 0)
{
//父节点的值小于孩子结点的值
//就交换
//if (_con[parent] < _con[child])
if (com(_con[parent], _con[child]))
{
swap(_con[parent], _con[child]);
//更新父亲和孩子的下标
child = parent;
parent = (child - 1) / 2;
}
else
{
break;
}
}
}
//插入
void push(const T& x)
{
//插入之后调用向上调整法
_con.push_back(x);
AdjustUp(_con.size() - 1);
}
//向下调整法
void AdjustDown(size_t parent)
{
compare com;
size_t child = parent * 2 + 1;
while (child < _con.size())
{
//我们这里是假定左孩子的值比较大
//因此我们需要将左孩子和右孩子的值比较一下
//更新一下
//if (child + 1 < _con.size() && _con[child] < _con[child + 1])
if (child + 1>_con.size() && com(_con[child], _con[child + 1]))
{
child++;
}
//if (_con[parent] < _con[child])
if (com(_con[parent], _con[child]))
{
swap(_con[parent], _con[child]);
parent = child;
child = parent * 2 + 1;
}
else
{
break;
}
}
}
//删除
void pop()
{
//将容器顶部与尾部的数据进行交换
swap(_con[0], _con[_con.size() - 1]);
_con.pop_back();
//调用向下调整算法
AdjustDown(0);
}
private:
Container _con;
};
}