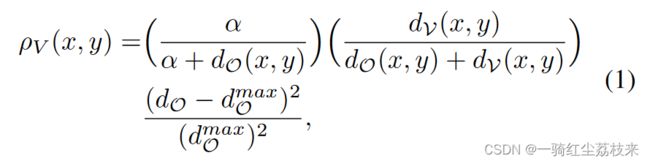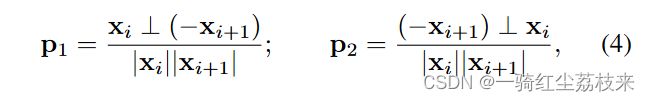【HybridAtar论文阅读笔记】【Practical Search Techniques in Path Planning for Autonomous Driving】
Practical Search Techniques in Path Planning for Autonomous Driving
Metadata
- CiteKey: PracticalSearchTechniques
- Type: journalArticle
- Title: Practical Search Techniques in Path Planning for Autonomous Driving,
- Author: Dolgov, Dmitri; Thrun, Sebastian; Montemerlo, Michael; Diebel, James,
Abstract
我们描述了一种实用的路径规划算法,该算法为在未知环境中运行的自动驾驶汽车生成了平稳的路径,在该环境中,机器人的传感器在线检测到障碍物。这项工作是受到2007年DARPA城市挑战赛的激励和实验验证的,机器人车必须自动驾驶停车场。我们的方法有两个主要步骤。第一步使用了众所周知的A搜索算法的变体,该变体应用于车辆的3D运动状态空间,但具有修改后的状态更高规则,可在A的离散节点中捕获车辆的连续状态。 (从而保证路径的运动可行性)。然后,第二步通过数字非线性优化提高了解决方案的质量,从而导致局部(且经常全局)最佳。斯坦福赛车队Junior在Urban Challenge中使用了本文所述的路径规划算法。初中表现出在复杂的一般路径规划任务中表现出完美的表现,例如在停车场导航和在被阻塞的道路上执行掉头,典型的饱满的重型时间为50-300ms。
We describe a practical path-planning algorithm that generates smooth paths for an autonomous vehicle operating in an unknown environment, where obstacles are detected online by the robot’s sensors. This work was motivated by and experimentally validated in the 2007 DARPA Urban Challenge, where robotic vehicles had to autonomously navigate parking lots. Our approach has two main steps. The first step uses a variant of the well-known A* search algorithm, applied to the 3D kinematic state space of the vehicle, but with a modified state-update rule that captures the continuous state of the vehicle in the discrete nodes of A* (thus guaranteeing kinematic feasibility of the path). The second step then improves the quality of the solution via numeric non-linear optimization, leading to a local (and frequently global) optimum. The path-planning algorithm described in this paper was used by the Stanford Racing Teams robot, Junior, in the Urban Challenge. Junior demonstrated flawless performance in complex general path-planning tasks such as navigating parking lots and executing U-turns on blocked roads, with typical fullcycle replaning times of 50–300ms.
Notes
1. 启发式值
算法使用的启发式算法并不是独有的,而是通用的。文章共使用了3种启发式进行测试:
(1)欧氏距离启发式——图a
(2)取欧氏距离和非完整无障碍代价的最大值的启发式——图b,c
(3)忽略非完整只考虑障碍的启发式与(2)的结合的启发式——图d
由图可知,单纯用欧几里得距离启发式,扩展了21515个节点(图a)。如果用非完整无障碍启发式,则拓展了1465个节点(图b)。但是非完整无障碍启发式在断头路会耗费很多及节点(图c)。通过非完整无障碍启发式和纯障碍启发式结合,可以将该问题解决(图d)
2. 节点拓展规则
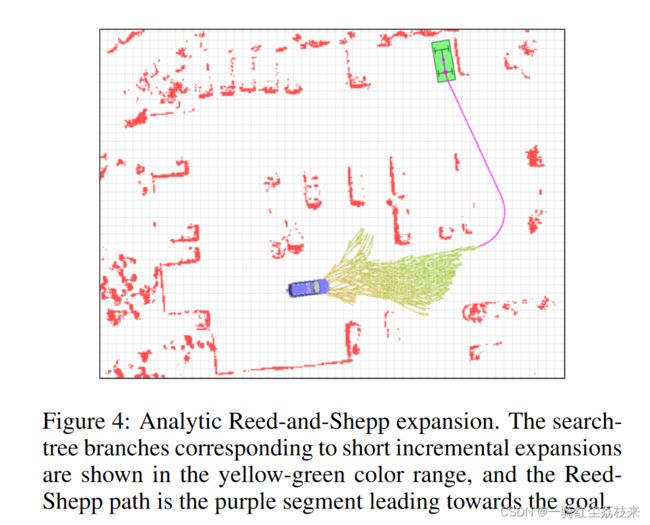
为了解决节点拓展时精度不够的问题,选择了reed-sheep曲线(下面简称为R-S曲线或R-S拓展)作为节点拓展的工具。
具体而言,在拓展一些节点时,通过计算从当前节点到目标节点的reed-shepp曲线来生成一个额外的节点。然后检查该路径是不是存在障碍物冲突,如果没有冲突,就将其增加到搜索树(closed表)中。
至于为什么是部分节点,而不是每个节点,作者认为,在远离目标的区域,大部分的路径都是有障碍物的,没有必要使用R-S拓展。作者采用的方法时:只从N个节点中选择1个节点拓展,而N随着距离目标的代价启发式函数值得增加而减小。
3. 路径代价的计算
3.1 定义维诺场
本文提出了维诺场(The Voronoi Field)的概念,用来计算障碍物代价。
公式中的定义:
d O ( x , y ) d_O(x,y) dO(x,y)代表(x,y)距离最近的障碍物(Fig.5(a))的距离
d V ( x , y ) d_V(x,y) dV(x,y)代笔(x,y)距离一般维诺图(GVD)(Fig.5(b))中最近的边的距离。
d O d_O dO 此处应当是 d O ( x , y ) d_O(x,y) dO(x,y),应该是作者笔误。
α \alpha α 是常数,用来控制图中最大影响范围的下降率。
d O m a x d_O^{max} dOmax 也是常数,用来控制场的最大影响范围。
需要注意的是,式(1)需要满足 d O ( x , y ) < = d O m a x d_O(x,y)<=d_O^{max} dO(x,y)<=dOmax,否则的话, ρ V ( x , y ) = 0 \rho_V(x,y)=0 ρV(x,y)=0
举个例子理解这个公式:如果(x,y)取图中蓝色的框标明的位置,那么 d V d_V dV值接近0,代价值很小。最极端的情况,(x,y)刚好位于一般维诺图的边缘上,此时 d V = 0 d_V=0 dV=0,那么整个代价 ρ V ( x , y ) \rho_V(x,y) ρV(x,y)也是0.
- 简单常规势场值计算公式——对应图Fig5(c)
ρ ( x , y ) = α ( α + d O ( x , y ) ) − 1 \rho(x,y)=\alpha(\alpha+d_O(x,y))^{-1} ρ(x,y)=α(α+dO(x,y))−1
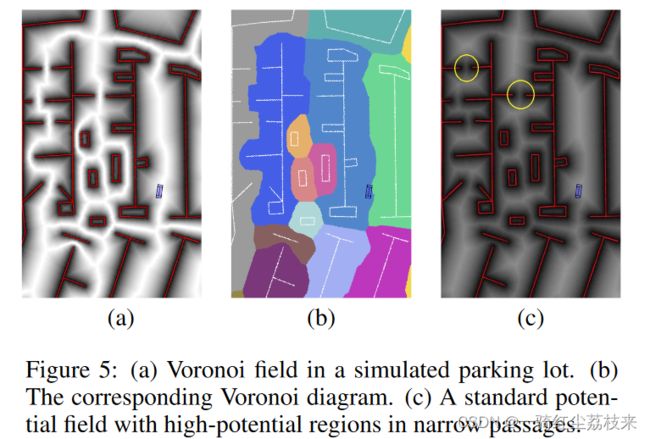
Fig5:(a)维诺场(2)维诺场对应的维诺图(3)常规势场
3.2 维诺场比常规势场的优势:
- 优势在于:
维诺场的势场值按照导航中全部可通行的间隙进行了比例缩放。即使狭窄的开口仍然可以导航。而常规的势场则不行。
例如在FIg.5中,(a)是维诺场的2维投影,(b)是相对广义的维诺图。注意到在障碍物之间,总是有一个连续的路径使得场值 ρ V ( x , y ) = 0 \rho_V(x,y)=0 ρV(x,y)=0。与(c)相比,在障碍物之间的狭窄的通道中,总是存在高场值的区域(黄色圆圈区域),会导致规划的时候无法通行。
3.3 维诺场与其他类似的场函数的比较
关于维诺图和势场,在机器人运动规划领域已经提出了很长时间了,例如( Sensor-based exploration: The hierarchical generalized voronoi graph)[[@doi10.117702783640022066770]]中使用分层广义维诺图(HGVG)来对机器人搜索路径。但是对于非完整性约束的汽车,直接使用维诺图规划不可行。本文并不是直接使用维诺场进行全局路径导航,但是注意到对于凸障碍空间,维诺场可以由全局吸引域增强,产生一个没有局部最小值的域,因此也可以适合于全局路径导航。
4. 路径的优化
- 可以尝试展示路径优化的过程
- 共轭梯度下降的概念了解:conjugate gradient (CG) descent
采用HybridAStar规划的路径是次优的,而且可能会存在不必要的突然转向,所以作者引入了后处理对路径进行优化。后处理分为两个阶段。
-
第一个阶段:非线性优化
在路径顶点坐标上制定了一个非线性优化程序,以改善路径长度和平滑度。 -
第二个阶段:非线性插值
第一个阶段得到的路径顶点之间仍然存在间隙,会导致突然转向,所以需要进行非参数的差值,使得路径顶点之间的曲率变化更加平缓。
4.1 第一个阶段:非线性优化
在路径顶点坐标上制定了一个非线性优化程序,以改善路径长度和平滑度。
4.1.1变量的定义:
顶点坐标序列: x i = ( x i , y i ) , i ⊂ [ 1 , N ] \boldsymbol{x_i}=(x_i,y_i),i\subset[1,N] xi=(xi,yi),i⊂[1,N]
障碍物接近顶点的位置: o i \boldsymbol{o_i} oi
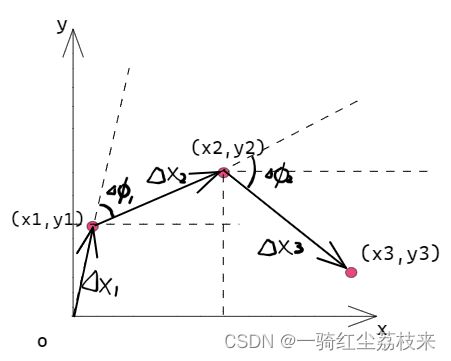
顶点移动向量: Δ x i = x i − x i − 1 \boldsymbol{\Delta{x_i}}=\boldsymbol{x_i}-\boldsymbol{x_{i-1}} Δxi=xi−xi−1
顶点处正切角度的变化量: Δ ϕ i = ∣ t a n − 1 Δ y i + 1 Δ x i + 1 − t a n − 1 Δ y i Δ x i ∣ \Delta{\phi_i}=|tan^{-1}\frac{\Delta{y_{i+1}}}{{\Delta{x_{i+1}}}}-tan^{-1}\frac{\Delta{y_{i}}}{{\Delta{x_{i}}}}| Δϕi=∣tan−1Δxi+1Δyi+1−tan−1ΔxiΔyi∣
![[@PracticalSearchTechniques_2022-06-30 17.11.16.excalidraw]]
4.1.2非线性优化的目标函数表达式:
F = w ρ ∑ i = 1 N ρ V ( x i , y i ) + w o ∑ i = 1 N σ o ( ∣ x i − o i ∣ − d max ) + w κ ∑ i = 1 N − 1 σ κ ( Δ ϕ i ∣ Δ x i ∣ − κ max ) + w s ∑ i = 1 N − 1 ( Δ x i + 1 − Δ x i ) 2 , \begin{aligned} &F=w_{\rho} \sum_{i=1}^{N} \rho_{V}\left(x_{i}, y_{i}\right)+w_{o} \sum_{i=1}^{N} \sigma_{o}\left(\left|\mathbf{x}_{i}-\mathbf{o}_{i}\right|-d_{\max }\right)+ \\ &w_{\kappa} \sum_{i=1}^{N-1} \sigma_{\kappa}\left(\frac{\Delta \phi_{i}}{\left|\Delta \mathbf{x}_{i}\right|}-\kappa_{\max }\right)+w_{s} \sum_{i=1}^{N-1}\left(\Delta \mathbf{x}_{i+1}-\Delta \mathbf{x}_{i}\right)^{2}, \end{aligned} F=wρi=1∑NρV(xi,yi)+woi=1∑Nσo(∣xi−oi∣−dmax)+wκi=1∑N−1σκ(∣Δxi∣Δϕi−κmax)+wsi=1∑N−1(Δxi+1−Δxi)2,
式中, ρ V \rho{V} ρV代表维诺场, κ m a x \kappa_{max} κmax代表路径允许的最大曲率(由车辆最小转弯半径定义), σ O , σ κ \sigma_O,\sigma_{\kappa} σO,σκ表示惩罚函数,作者经验性的取了二次惩罚函数。wρ, wo, wκ, ws都是权重。
4.1.3下面把目标函数表达式分解成4个部分进行解释:
(1)第一个部分:维诺场值
w ρ ∑ i = 1 N ρ V ( x i , y i ) w_{\rho} \sum_{i=1}^{N} \rho_{V}\left(x_{i}, y_{i}\right) wρi=1∑NρV(xi,yi)
这一部分是维诺场值,维诺场值的加入,使得无论是在狭窄的通道还是宽敞的通道,都可以让规划的路径尽可能远离障碍物。
(2)第二个部分:障碍物距离惩罚项
w o ∑ i = 1 N σ o ( ∣ x i − o i ∣ − d max ) w_{o} \sum_{i=1}^{N} \sigma_{o}\left(\left|\mathbf{x}_{i}-\mathbf{o}_{i}\right|-d_{\max }\right) woi=1∑Nσo(∣xi−oi∣−dmax)
这一部分主要是各个顶点到最近的障碍物的距离减去 d max d_{\max } dmax,然后乘以惩罚函数,再累加起来。这里 d max d_{\max } dmax的含义是什么,文章没有明确说明。个人猜测它的含义是:能够允许的路径点到障碍物的最大距离,这个需要根据实际需要人为的调整, d max d_{\max } dmax越小,意味着规划出来的路径越贴近障碍物, d max d_{\max } dmax越大,意味着规划的路径越远离障碍物。
按照这个理解,如果 ∣ x i − o i ∣ = d m a x |\mathbf{x}_{i}-\mathbf{o}_{i}|=d_{max} ∣xi−oi∣=dmax,意味着路径点到最近的障碍物的距离正好等于我们设定的最大距离,此时 σ o ( . . . ) \sigma_{o}(...) σo(...)取得最小值。就没有惩罚。只要 ∣ x i − o i ∣ ≠ d m a x |\mathbf{x}_{i}-\mathbf{o}_{i}|\neq d_{max} ∣xi−oi∣=dmax, σ o ( . . . ) \sigma_{o}(...) σo(...)项就>0,就会产生惩罚。
所以这一项的优化结果就是让每个顶点距离最近的障碍物的值尽可能等于设定的值。避免与障碍物碰撞。
(3)第三个部分:曲率惩罚项
w κ ∑ i = 1 N − 1 σ κ ( Δ ϕ i ∣ Δ x i ∣ − κ max ) w_{\kappa} \sum_{i=1}^{N-1} \sigma_{\kappa}\left(\frac{\Delta \phi_{i}}{\left|\Delta \mathbf{x}_{i}\right|}-\kappa_{\max }\right) wκi=1∑N−1σκ(∣Δxi∣Δϕi−κmax)
其中 Δ ϕ i ∣ Δ x i ∣ \frac{\Delta \phi_{i}}{\left|\Delta \mathbf{x}_{i}\right|} ∣Δxi∣Δϕi这一项求的就是这一段路径的瞬时曲率。和第二项类似,第三项的优化结果是让每个顶点的瞬时曲率都尽可能接近设定的最大瞬时曲率值。避免路径曲率变化过于快。
(4)第四个部分:平滑项
w s ∑ i = 1 N − 1 ( Δ x i + 1 − Δ x i ) 2 w_{s} \sum_{i=1}^{N-1}\left(\Delta \mathbf{x}_{i+1}-\Delta \mathbf{x}_{i}\right)^{2} wsi=1∑N−1(Δxi+1−Δxi)2
这一项是要求各个顶点之间的距离变化尽可能小,整体上体现为路径更加的平滑。
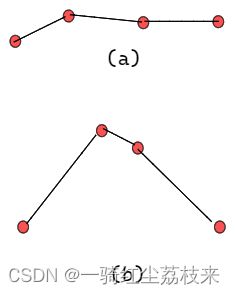
例如下图中,(a)中各个顶点的距离变化较小, 整体就比较平滑。(b)中顶点的距离变化很大,整体就比较不平滑。
图:(a)和(b)分别代表了两种曲线,(a)平滑(b)不平滑
4.1.4 计算目标函数的梯度
(1)维诺场部分的梯度计算
这里就是各种求偏导,计算过程就不赘述了。
- 有意思的是第二个式子导出来就与 O i X i O_iX_i OiXi向量同方向的一个单位向量。没搞明白什么意思。
- 另外第一个式子右边应该有一个1/2。而且为什么要多此一举,凑了两项出来。也没明白。

(2)障碍物惩罚部分的梯度计算
如果 ∣ x i − o i ∣ < = d m a x |x_{i}-o_{i}|<=d_{max} ∣xi−oi∣<=dmax,那么惩罚函数 σ o ( . . . ) \sigma_{o}(...) σo(...)的梯度可以表示为:

这个结果还是一个向量:长度是 2 x( ∣ x i − o i ∣ − d m a x |x_{i}-o_{i}|-d_{max} ∣xi−oi∣−dmax);方向是Oi指向Xi的方向。
可以看到,梯度的方向是负的,也就是惩罚函数是在减小的, ∣ x i − o i ∣ |x_{i}-o_{i}| ∣xi−oi∣与 d m a x d_{max} dmax的差值越大,梯度越大,下降速度越快。
(3)最大曲率的惩罚项
在计算中,我们必须对影响曲率的3个节点进行采样,节点i的正切角的变化值最好的表示形式为:

这个表达式其实就是求 Δ x i \Delta x_i Δxi与 Δ x i + 1 \Delta x_{i+1} Δxi+1的向量的夹角。最初给出的定义是通过反正切函数计算的,而这个表达式更为直接,直接通过反余弦函数计算。具体可以看上面的 图:优化使用坐标举例去理解。
式(2)可以转化为:
cos Δ ϕ i = Δ X i ⊤ Δ X i + 1 ∣ Δ X i ∣ ∣ Δ X i + 1 ∣ \cos \Delta \phi_{i}=\frac{\Delta X_{i}^{\top} \Delta X_{i+1}}{\left|\Delta X_{i}\right|\left|\Delta X_{i+1}\right|} cosΔϕi=∣ΔXi∣∣ΔXi+1∣ΔXi⊤ΔXi+1
下面求偏导的式子中也用了 cos Δ ϕ i \cos \Delta \phi_{i} cosΔϕi来表示后面那个值。
然后节点i的瞬时曲率表示为: κ i = Δ ϕ i / ∣ Δ x i ∣ \kappa_i=\Delta\phi_i / |\Delta x_i| κi=Δϕi/∣Δxi∣,
根据前面的定义,还知道 Δ x i = x i − x i − 1 \boldsymbol{\Delta{x_i}}=\boldsymbol{x_i}-\boldsymbol{x_{i-1}} Δxi=xi−xi−1, Δ x i + 1 = x i + 1 − x i \boldsymbol{\Delta{x_{i+1}}}=\boldsymbol{x_{i+1}}-\boldsymbol{x_{i}} Δxi+1=xi+1−xi, 然后可以带入求偏导,进一步表示为:

式子中涉及到 cos Δ ϕ i \cos \Delta \phi_{i} cosΔϕi对三个顶点 x i , x i − 1 , x i + 2 x_i,x_{i-1},x_{i+2} xi,xi−1,xi+2的导数,这三个导数用正交补的形式表示最容易:

4.1.5 优化的流程(补缺)
这个论文中没有提及。第一阶段给出了一个目标函数F。我们的优化问题就可以定义为:
找到一系列的目标点(x,y),使得这个目标函数F能够取得极小值。这一些系列的目标点(x,y)就是优化后的路径。
4.1.6 优化示例
从Fig.7中可以看出,经过第一阶段的优化,可以让路径更加平滑、远离障碍物。

4.2 第二个阶段 非参数插值
经过第一阶段的优化,整个路径看起来已经非常平滑了,但是路径的顶点之间会有0.5m-1m的间隙。如果不进行差值,会导致车辆在一个顶点到下一个顶点时猛打方向。所以为了使得车辆能够走得更加平顺,还需要进行插值。作者认为一些参数插值(拉格朗日插值法、三次Hermite插值、牛顿插值法、三次样条插值法)对噪声很敏感,例如对于三次样条插值法,如果输入的几个节点位置非常接近,会导致输出出现很大的振荡。
这里采用了非参数差值方法,通过新增顶点来对路径进行超采样。使用共轭梯度下降法来最小化路径的曲率,同时保持原有路径的顶点位置不变。
5. 实验结果
算法在DARPA城市挑战赛上进行了应用。
5.1规划的参数
- 障碍图:160m x 160m, 分辨率0.15cm,
- A ∗ A* A∗使用的栅格:160x160x360°,x-y上分辨率为0.5m,角度 θ \theta θ上分辨率为5°。
- 重规划流程:A星搜索,CG平滑,插值
- 重规划时间:50-300ms
5.2 结果展示
Fig9:(a)和(b)都是断头路U型掉头。(c)是执行停车任务。
![[Pasted image 20220701114821.png]]
6.论文涉及到的知识点学习
论文中有很多作者一笔带过的知识,但是如果不深入了解,就无法掌握算法的精髓。
例如:
- 共轭梯度下降法(CG)
- 非参数插值方法
6.1 共轭梯度下降法方法
首先给出参考学习资料:
- 博客:【数值分析 2.2】Conjugate Gradient - 知乎 (zhihu.com)
- 论文:An introduction to the conjugate gradient method without the agonizing pain 链接: painless-conjugate-gradient.pdf (cmu.edu)
7.拓展论文阅读:
根据参考博客:Hybrid A*论文解析(1)_gophae的博客-CSDN博客
筛选出以下HybridAtar的拓展论文阅读:
-
同一个作者Dolgov的其他工作:Autonomous driving in semi-structured environments: Mapping and planning(2009)
摘要 - 我们考虑在半结构化环境(例如停车场)中自动驾驶的问题。这样的环境具有强大的拓扑结构(可驱动的车道的图),但是与这些图形显着偏差的操纵是有效且频繁的。我们解决了在这种环境中操作的两个主要挑战:i)传感器数据中检测拓扑结构,ii)使用该结构指导路径计划。我们介绍了这两个主题的实验结果,证明了对停车场中车道网络的强大估计以及使用这些拓扑网络指导路径计划的好处 -
伯克利的Xiaojing Zhang的工作:Autonomous Parking using Optimization-Based Collision Avoidance(2018)
总结 - 这个工作主要是针对自动泊车问题,提出了分层的基于优化的避障算法(Hierarchical optimization-based collision avoidance,H-OBCA)。H-OBCA算法是使用HybridAtar生成初始路径,然后使用OBCA方法优化和平滑路径。
摘要 - 我们提出了一种基于优化的自动停车方法。在基于优化的避免碰撞(OBCA)领域的最新进展的基础上,我们表明自主停车问题可以作为平滑的非凸优化问题提出。不幸的是,此类问题在数字上是具有挑战性的,通常需要适当的温暖启动。为了解决这一限制,我们提出了一种名为“等级OBCA(HOBCA)”的新型算法。主要思想是首先使用通用路径计划器,例如混合A?,以使用简化的车辆模型来计算粗轨迹,并通过离散状态输入空间来计算。随后,该路径用于温暖OBCA算法,该算法使用完整的车辆模型和连续优化来优化和平滑粗路。我们的研究表明,拟议的H-OBCA停车算法将混合动力A?的全球路径计划功能与OBCA产生平滑,无碰撞和动态可行的路径的能力相结合。广泛的模拟表明,拟议的H-OBCA算法是强大的,并承认自动驾驶汽车的实时停车。示例代码可在https://github.com/xiaojinggeorgezhang/ h-obca提供。 -
Xiaojing Zhang的另一个工作:Optimization-Based Collision Avoidance(2021)
摘要 - 本文提出了一种新的方法,可以精确地将非不同的避免碰撞限制用于使用凸优化的强双重性,从而将非不同的碰撞约束限制为平滑的,可不同的约束。我们专注于一个受控的对象,其目标是在n维空间中移动时避免障碍。拟议的重新制定是准确的,不引入任何近似值,并且适用于可以表示为凸组合的一般障碍和受控物体。我们将结果与签名距离的概念联系起来,该距离广泛用于传统轨迹生成算法。我们的方法可以应用于通用导航和轨迹计划任务,并且平滑度属性允许使用通用梯度和基于黑森的优化算法。最后,如果无法避免碰撞,我们的框架使我们能够找到以渗透率来衡量的“最小侵入性”轨迹。我们证明了我们的框架对自动停车问题的功效,我们的数值实验表明该方法是可靠的,并且可以在紧密的环境中启用基于实时优化的轨迹计划。我们的示例代码提供https://github.com/xiaojinggeorgezhang/obca上。