【数据挖掘】主成分分析Python实现

前言

是对一个数据挖掘作业的记录，数据集是老师提供的几种癌症的数据，我是直接在Jupyter中写的，中间会输出一些内容验证之类的

主要是参照这位写的：参考的大佬

数据预处理

导入库

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt

读取数据

# 读取数据，查看数据的规模
BLCA_data = pd.read_csv(r'数据集/BLCA/rna.csv')
print('BLCA',BLCA_data.shape)
BRCA_data = pd.read_csv(r'数据集/BRCA/rna.csv')
print('BRCA',BRCA_data.shape)
KIRC_data = pd.read_csv(r'数据集/KIRC/rna.csv')
print('KIRC',KIRC_data.shape)
LUAD_data = pd.read_csv(r'数据集/LUAD/rna.csv')
print('LUAD',LUAD_data.shape)
PAAD_data = pd.read_csv(r'数据集/PAAD/rna.csv')
print('PAAD',PAAD_data.shape)

BLCA (3217, 400)
BRCA (3217, 1032)
KIRC (3217, 489)
LUAD (3217, 491)
PAAD (3217, 177)

# 查看其中一种类型癌症数据集的前6行
BLCA_data.head(6)

	gene_id	TCGA-HQ-A2OF	TCGA-GU-A767	TCGA-ZF-AA4R	TCGA-DK-A1AC	TCGA-DK-A3IT	TCGA-GC-A3RD	TCGA-BT-A0YX	TCGA-FD-A6TE	TCGA-E7-A5KE	...	TCGA-BT-A0S7	TCGA-K4-A6FZ	TCGA-E5-A2PC	TCGA-DK-AA6Q	TCGA-XF-AAMY	TCGA-CU-A0YO	TCGA-E7-A7PW	TCGA-S5-A6DX	TCGA-GD-A76B	TCGA-ZF-AA4V
0	A2BP1|54715	-0.402918	-1.236959	-1.453230	-1.211589	-1.288438	-1.262086	-1.033565	-1.183245	-1.076254	...	-1.282740	-1.023637	-0.366722	-1.161285	-1.380649	-1.205136	-0.875586	-1.059148	-1.393928	-1.215641
1	A2ML1|144568	0.717502	0.737891	1.584643	1.471932	0.414015	1.821084	2.515898	0.723830	0.668703	...	0.163903	1.318229	0.879135	0.513603	1.571557	1.679199	1.222708	-0.079802	1.480393	1.947340
2	ACTL6B|51412	-1.185185	-1.403906	-1.453230	-1.211589	-1.288438	-1.262086	-1.196075	-1.183245	-0.937518	...	-1.282740	-1.291842	-1.036778	-1.161285	-1.380649	-1.368904	-1.567590	-1.425863	-1.393928	-1.215641
3	ADAM6|8755	0.373826	1.411279	2.092282	3.186438	2.967457	1.437113	2.723775	2.320012	0.736963	...	2.375413	1.964369	1.202000	1.824419	2.185051	2.175849	1.446352	3.591872	3.266818	2.514385
4	ADAMDEC1|27299	-0.489828	-0.894004	-0.205169	1.015179	0.089540	0.114903	0.664465	0.138955	-1.076254	...	-0.408256	-0.063113	-0.147173	0.177490	-0.254007	0.173888	-0.951712	0.592750	0.260382	0.758897
5	ALDH1A3|220	0.420170	0.563404	1.064257	0.460861	1.518204	1.809320	1.230912	1.488275	0.809302	...	1.180098	1.751919	0.034835	1.512029	0.851459	1.645271	0.398217	0.599149	-0.064256	1.339531

6 rows × 400 columns

# 查看另一种癌症数据集的前6行
BRCA_data.head(6)

	gene_id	TCGA-D8-A1XJ	TCGA-EW-A6SA	TCGA-D8-A27H	TCGA-E9-A247	TCGA-AC-A2FG	TCGA-B6-A0RP	TCGA-BH-A0DH	TCGA-AN-A0AM	TCGA-D8-A1XZ	...	TCGA-BH-A18G	TCGA-E2-A15J	TCGA-BH-A1F6	TCGA-EW-A1P8	TCGA-AO-A1KT	TCGA-A2-A0D0	TCGA-3C-AALK	TCGA-AO-A1KS	TCGA-EW-A1OW	TCGA-OL-A5RU
0	A2BP1|54715	-1.069946	-1.075002	-1.377040	-1.307689	-1.292405	-1.231926	-1.231272	-1.396638	-1.229635	...	-1.079587	-1.018372	-1.355431	-1.156045	-1.337455	-1.189837	-1.467466	-1.339815	-1.315667	-1.421373
1	A2ML1|144568	0.255748	-0.877250	1.623317	-1.307689	-0.718106	-1.135720	-1.231272	0.253569	0.136528	...	-0.496468	-1.135840	1.870474	0.995603	-0.732074	-0.500924	-1.075625	-0.708317	0.481910	-0.781841
2	ACTL6B|51412	-1.253764	-1.075002	-1.377040	-1.307689	-1.458347	-1.231926	-1.231272	-1.396638	-1.229635	...	-1.079587	-1.135840	-1.200037	-1.277135	-1.337455	-1.189837	-1.467466	-1.339815	-1.162777	-1.421373
3	ADAM6|8755	1.949321	2.603630	2.016646	1.936839	2.851206	2.159315	3.494672	2.665196	3.116796	...	1.503065	1.523513	3.238382	2.476680	2.039449	1.642455	2.529546	1.563575	2.519419	3.503925
4	ADAMDEC1|27299	-0.219076	-0.343607	-0.110169	0.410611	-0.181777	-0.254802	-0.000519	0.218526	0.521942	...	-0.027635	0.073684	1.214923	0.885440	-0.145622	0.466923	0.330690	0.485908	0.684071	0.723861
5	ALDH1A3|220	1.138533	0.290696	2.239296	0.755849	1.327123	0.740471	1.101451	1.091598	0.884671	...	2.251904	1.135105	1.978201	1.827946	0.834657	1.252129	1.159214	0.949791	1.215054	0.805760

6 rows × 1032 columns

经过上面的分析可以知道对于不同的数据集，它们的行数和行标签都是相同的，但列数和列标签都是不同的
所以对于这些数据集来说，行标签可以看作是数据的不同特征，而每一列则对应一个样本的数据

保留第一个数据集的第一列，然后将其与后面几个数据集除第一列之外的列进行合并
则：

BLCA:1-400

BRCA:401-1431

KIRC:1432-1919

LUAD:1920-2409

PAAD:2410-2585

将五种癌症数据集合并

# 将5种癌症数据集的除gene_id列之外的列进行合并
DataSet = pd.concat([BLCA_data,BRCA_data.iloc[:,1:],KIRC_data.iloc[:,1:],LUAD_data.iloc[:,1:],PAAD_data.iloc[:,1:]], axis=1)
DataSet.head(6)

	gene_id	TCGA-HQ-A2OF	TCGA-GU-A767	TCGA-ZF-AA4R	TCGA-DK-A1AC	TCGA-DK-A3IT	TCGA-GC-A3RD	TCGA-BT-A0YX	TCGA-FD-A6TE	TCGA-E7-A5KE	...	TCGA-FB-A7DR	TCGA-H8-A6C1	TCGA-LB-A8F3	TCGA-IB-7893	TCGA-2J-AABF	TCGA-US-A77J	TCGA-F2-7273	TCGA-HZ-A8P0	TCGA-3A-A9IH	TCGA-2L-AAQA
0	A2BP1|54715	-0.402918	-1.236959	-1.453230	-1.211589	-1.288438	-1.262086	-1.033565	-1.183245	-1.076254	...	-1.046787	-1.561721	-1.256692	-1.345364	-1.279792	-1.621289	-1.054519	-1.455548	-1.464518	-1.471927
1	A2ML1|144568	0.717502	0.737891	1.584643	1.471932	0.414015	1.821084	2.515898	0.723830	0.668703	...	-1.226226	-0.680184	-1.038366	1.252544	-0.752025	-1.621289	-1.504779	0.680993	0.666947	-0.915410
2	ACTL6B|51412	-1.185185	-1.403906	-1.453230	-1.211589	-1.288438	-1.262086	-1.196075	-1.183245	-0.937518	...	-1.126668	-1.141486	-0.768676	-1.013273	-0.542150	-0.338250	-0.368487	-1.455548	-0.454760	-1.471927
3	ADAM6|8755	0.373826	1.411279	2.092282	3.186438	2.967457	1.437113	2.723775	2.320012	0.736963	...	2.500539	2.534327	1.895497	2.523738	2.771487	3.508540	2.503007	3.031195	2.018857	2.171331
4	ADAMDEC1|27299	-0.489828	-0.894004	-0.205169	1.015179	0.089540	0.114903	0.664465	0.138955	-1.076254	...	0.381645	0.286921	-0.266635	-0.161585	0.380947	0.772060	0.254188	-0.122049	-0.596158	0.098888
5	ALDH1A3|220	0.420170	0.563404	1.064257	0.460861	1.518204	1.809320	1.230912	1.488275	0.809302	...	1.530532	1.107393	0.618689	1.232431	1.062113	1.035272	1.220392	1.052504	0.985869	0.812195

6 rows × 2585 columns

对数据集进行转置，之后每一行对应一个样本数据，每一列表示一个样本特征

DataSet = DataSet.T
DataSet.head(6)

	0	1	2	3	4	5	6	7	8	9	...	3207	3208	3209	3210	3211	3212	3213	3214	3215	3216
gene_id	A2BP1|54715	A2ML1|144568	ACTL6B|51412	ADAM6|8755	ADAMDEC1|27299	ALDH1A3|220	ATCAY|85300	ATP10B|23120	BCAS1|8537	C10orf105|414152	...	SLC38A5|92745	SLC44A3|126969	SSX4|6759	TMEM200B|399474	TMEM26|219623	TNFRSF10D|8793	XAF1|54739	YJEFN3|374887	ZMAT1|84460	ZNF415|55786
TCGA-HQ-A2OF	-0.402918	0.717502	-1.185185	0.373826	-0.489828	0.42017	-1.185185	1.841492	1.327818	-0.301422	...	0.275846	1.228001	-0.959773	-0.530559	0.637047	1.339706	0.520305	0.235093	-0.383992	0.795605
TCGA-GU-A767	-1.236959	0.737891	-1.403906	1.411279	-0.894004	0.563404	-1.236959	1.309958	2.015829	0.416162	...	0.364331	1.484526	-1.403906	0.689511	-0.474266	0.378506	0.994647	0.776598	0.334363	0.577015
TCGA-ZF-AA4R	-1.45323	1.584643	-1.45323	2.092282	-0.205169	1.064257	-1.267946	0.207475	0.764633	-0.786075	...	1.350011	1.03154	-1.45323	0.867536	-0.145515	0.22999	1.210068	0.303078	0.91272	0.70952
TCGA-DK-A1AC	-1.211589	1.471932	-1.211589	3.186438	1.015179	0.460861	-0.995834	1.576376	0.546906	-0.855604	...	0.637691	1.190068	-0.348651	0.034641	0.030973	0.09397	1.089523	0.583813	0.503198	0.733853
TCGA-DK-A3IT	-1.288438	0.414015	-1.288438	2.967457	0.08954	1.518204	-1.159105	-0.035145	1.575849	0.220414	...	0.598191	1.479815	-1.288438	0.921235	-0.3077	0.486069	1.311523	0.483139	0.262508	0.589681

6 rows × 3217 columns

# 此时第一行为特征标签，将非数据的这一行去掉
DataSet = DataSet.iloc[1:,:]

DataSet.iloc[:6,:]

	0	1	2	3	4	5	6	7	8	9	...	3207	3208	3209	3210	3211	3212	3213	3214	3215	3216
TCGA-HQ-A2OF	-0.402918	0.717502	-1.185185	0.373826	-0.489828	0.420170	-1.185185	1.841492	1.327818	-0.301422	...	0.275846	1.228001	-0.959773	-0.530559	0.637047	1.339706	0.520305	0.235093	-0.383992	0.795605
TCGA-GU-A767	-1.236959	0.737891	-1.403906	1.411279	-0.894004	0.563404	-1.236959	1.309958	2.015829	0.416162	...	0.364331	1.484526	-1.403906	0.689511	-0.474266	0.378506	0.994647	0.776598	0.334363	0.577015
TCGA-ZF-AA4R	-1.453230	1.584643	-1.453230	2.092282	-0.205169	1.064257	-1.267946	0.207475	0.764633	-0.786075	...	1.350011	1.031541	-1.453230	0.867536	-0.145515	0.229990	1.210068	0.303078	0.912720	0.709520
TCGA-DK-A1AC	-1.211589	1.471932	-1.211589	3.186439	1.015179	0.460861	-0.995834	1.576376	0.546906	-0.855604	...	0.637691	1.190068	-0.348651	0.034641	0.030973	0.093970	1.089523	0.583813	0.503198	0.733853
TCGA-DK-A3IT	-1.288438	0.414015	-1.288438	2.967457	0.089540	1.518204	-1.159105	-0.035145	1.575849	0.220414	...	0.598191	1.479815	-1.288438	0.921235	-0.307700	0.486069	1.311522	0.483139	0.262508	0.589681
TCGA-GC-A3RD	-1.262087	1.821084	-1.262087	1.437113	0.114903	1.809320	-0.993603	0.878451	2.058253	0.036055	...	1.069556	1.383669	-0.215558	0.234100	-0.324477	0.379689	1.323748	-0.026147	0.638123	0.096817

6 rows × 3217 columns

# 重新设置数据类型，此时DataSet为一个2584x3217的浮点数矩阵
DataSet = DataSet.astype('float32')
print(DataSet.shape)

(2584, 3217)

进行主成分分析

计算样本均值

Mean_vec = np.mean(DataSet, axis=0)
print('样本的均值:\n',Mean_vec)

样本的均值:
 0      -1.161548
1      -0.474133
2      -1.251174
3       2.412248
4       0.266737
          ...   
3212    0.521786
3213    1.303051
3214    0.133573
3215    0.774802
3216    0.601425
Length: 3217, dtype: float32

计算样本协方差矩阵

'''
# 纯数据运算
Cov_mat = (DataSet-Mean_vec).T.dot(DataSet-Mean_vec)/(DataSet.shape[0]-1)
print('协方差矩阵:\n',Cov_mat)
'''

# 使用numpy中计算协方差的函数
'''
协方差矩阵用于衡量两个变量之间相互依赖的程度
由于有3217个feature,故协方差矩阵的规模为3217x3217
'''
Cov_mat = np.cov(DataSet.T)
print('样本协方差矩阵:\n',Cov_mat)
Cov_mat.shape

样本协方差矩阵:
 [[ 0.12676448 -0.02361515  0.02157561 ...  0.00519793  0.00904992
   0.00673015]
 [-0.02361515  1.00118482 -0.0053748  ...  0.07527039 -0.17714864
   0.0090866 ]
 [ 0.02157561 -0.0053748   0.13757093 ...  0.00533166 -0.00134267
   0.00309703]
 ...
 [ 0.00519793  0.07527039  0.00533166 ...  0.22596547  0.02969978
   0.01703536]
 [ 0.00904992 -0.17714864 -0.00134267 ...  0.02969978  0.20364439
   0.04410373]
 [ 0.00673015  0.0090866   0.00309703 ...  0.01703536  0.04410373
   0.13098872]]
(3217, 3217)

计算特征值和特征向量

EigenValues, EigenVector = np.linalg.eig(Cov_mat)
# 数据特征量较大，这里计算结果为复数，统一取其实部
EigenValues = EigenValues.real
EigenVector = EigenVector.real
print('特征值:\n',EigenValues)
print('特征向量:\n',EigenVector)

特征值:
 [ 2.31279350e+02  1.46770122e+02  8.81143724e+01 ...  2.86122668e-17
  2.84073038e-17 -3.12152010e-17]
特征向量:
 [[ 0.00030864 -0.00113702 -0.00123991 ... -0.00242919 -0.00277321
   0.00190791]
 [-0.02456387  0.02533867 -0.05603828 ...  0.00124872  0.00140361
  -0.00075202]
 [-0.00023562 -0.00033786 -0.00340553 ... -0.00034539 -0.00039286
   0.00087827]
 ...
 [-0.00238575  0.00450426 -0.01746374 ... -0.00422026 -0.00422903
   0.00272333]
 [ 0.00781593 -0.02092816  0.00775456 ...  0.01314091  0.01272775
   0.01905482]
 [-0.0030166  -0.01263667 -0.0111954  ...  0.02344654  0.03139416
   0.01099676]]

# EigenPairs[i][0]表示一个特征值，EigenPairs[i][1]表示该特征值所对应的特征向量
EigenPairs = [(np.abs(EigenValues[i]), EigenVector[:,i]) for i in range(len(EigenValues))]

EigenPairs.sort(key=lambda x:x[0], reverse=True)
print('特征值降序排列:')
for i in EigenPairs:
    print(i[0])

特征值降序排列:
231.2793503404339
146.77012152572306
88.11437236590861
......
1.6398199526831266e-18
1.4276145590349296e-18
1.4276145590349296e-18

计算累计方差贡献率

# 计算方差贡献率
tot = sum(EigenValues)
var_exp = [(i/tot)*100 for i in sorted(EigenValues, reverse=True)]
print(var_exp)
# 累计方差贡献率
Cum_var_exp = np.cumsum(var_exp)
Cum_var_exp

[18.501009256397158, 11.740760136661512, ... , -1.3125279499634018e-16, -2.0754934203007648e-16]
array([ 18.50100926,  30.24176939,  37.29040913, ...,  100.,  100. ,  100.])

特征向量选取

## 这里为方便作图，选取特征值较大的前两维的特征向量
Matrix = np.hstack((EigenPairs[0][1].reshape(DataSet.shape[1], 1),
                    EigenPairs[1][1].reshape(DataSet.shape[1], 1)))
print('Matrix:\n',Matrix)

Matrix:
 [[ 0.00030864 -0.00113702]
 [-0.02456387  0.02533867]
 [-0.00023562 -0.00033786]
 ...
 [-0.00238575  0.00450426]
 [ 0.00781593 -0.02092816]
 [-0.0030166  -0.01263667]]

结果可视化

数据降维

# tmp主要是将DaraSet转成array类型
HighDimSet = DataSet.iloc[:,:].values
# 将原数据矩阵乘以选取的特征向量进行降维
LowDimSet = HighDimSet.dot(Matrix)
LowDimSet

array([[ -2.78179211,   7.81840477],
       [-13.39504631,   7.30085955],
       [-16.8183728 ,   3.87839756],
       ...,
       [ -5.81835218,   8.30323684],
       [ -8.52738732,   8.17363152],
       [ -6.97177986,  11.89669388]])

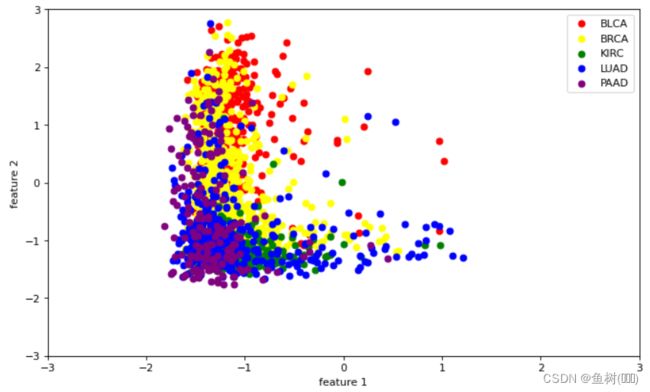
降维前

# LabelSet标识哪一行样本属于哪种癌症
LabelSet = ['BLCA']*399+['BRCA']*1031+['KIRC']*488+['LUAD']*490+['PAAD']*176
LabelSet = np.array(LabelSet)
LabelSet

array(['BLCA', 'BLCA', 'BLCA', ..., 'PAAD', 'PAAD', 'PAAD'], dtype='

# 选取两种特征对不同的癌症种类进行区分
plt.figure(figsize=(10,6), dpi=80)
plt.xlim(-3,3)
plt.ylim(-3,3)
for lab,color in zip(('BLCA', 'BRCA', 'KIRC', 'LUAD', 'PAAD'),
                     ('red','yellow','green','blue','purple')):
    plt.scatter(HighDimSet[LabelSet==lab,0],
                HighDimSet[LabelSet==lab,1],
                label=lab,c=color)
plt.xlabel('feature 1')
plt.ylabel('feature 2')
plt.legend(loc='upper right')
plt.show()

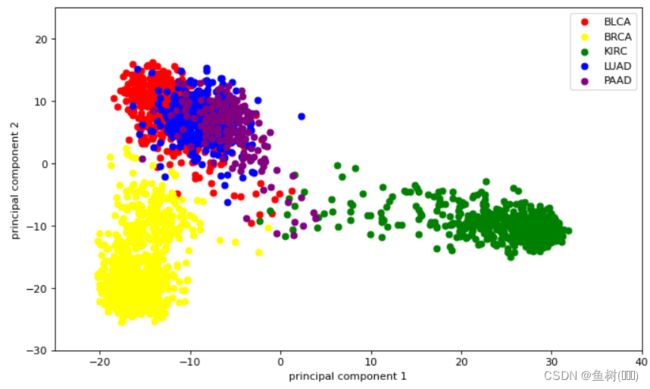
降维后

plt.figure(figsize=(10,6), dpi=80)
plt.xlim(-25,40)
plt.ylim(-30,25)
for lab,color in zip(('BLCA', 'BRCA', 'KIRC', 'LUAD', 'PAAD'),
                     ('red','yellow','green','blue','purple')):
    plt.scatter(LowDimSet[LabelSet==lab,0],
                LowDimSet[LabelSet==lab,1],
               label=lab,c=color)
plt.xlabel('principal component 1')
plt.ylabel('principal component 2')
plt.legend(loc='upper right')
plt.show()

写在最后

文章仅作记录，至于原理还有很多不懂的地方，结果我也不知道该是什么样的，把用这么多维特征来区分的事物降到两维来进行区分，我自己感觉已经很神奇了哈哈！