Physics-informed dynamic mode decomposition
Physics-informed dynamic mode decomposition (piDMD)
- Peter J. Baddoo∗1, Benjamin Herrmann, Beverley J. McKeon, J. Nathan Kutz, and Steven L. Brunton
- 1Department of Mathematics, Massachusetts Institute of Technology, Cambridge, MA 02139, USA
- 2021
- arxiv
- 代码地址(www.github.com/baddoo/piDMD.)
文章目录
- Physics-informed dynamic mode decomposition (piDMD)
- 摘要
- Mathematical background
-
- Dynamic mode decomposition
- Procrustes problems
- Physics-informed dynamic mode decomposition (piDMD)
- Applying piDMD to enforce canonical physical structures
-
- Shift-invariant systems(平移不变形)为例
- Experiment
摘要
- In this work, we demonstrate how physical principles – such as symmetries, invariances, and conservation laws – can be integrated into the dynamic mode decomposition (DMD).
- However, DMD frequently produces models that are sensitive to noise, fail to generalize outside the training data, and violate basic physical laws.
- Our physics-informed DMD (piDMD) optimization, which may be formulated as a Procrustes problem(正交普鲁克问题,一个最小平方矩阵近似问题), restricts the family of admissible models to a matrix manifold (矩阵流形) that respects the phys- ical structure of the system. We focus on five fundamental physical principles – conservation, self-adjointness, localization, causality, and shift-invariance – and derive several closed-form solutions and efficient algorithms for the corresponding piDMD optimizations.
- With fewer de- grees of freedom, piDMD models are less prone to overfitting, require less training data, and are often less computationally expensive to build than standard DMD models.
Mathematical background
Dynamic mode decomposition
介绍
线性系统
d x d t = K x \frac{d x}{d t}=K x dtdx=Kx
利用简单的数值方法(比如欧拉法)将其离散化,可以得到
x k + 1 = A x k x_{k+1}=A x_{k} xk+1=Axk
其中,矩阵 A A A与 K K K是相关的,上式的通解为 y = C e x y=Ce^{x} y=Cex。上式可以记录 X ( n − 1 ) = [ x 0 , x 1 , … , x n − 1 ] , X ( n ) = [ x 1 , x 2 , … , x n ] X^{(n-1)}=\left[x_{0}, x_{1}, \ldots, x_{n-1}\right], X^{(n)}=\left[x_{1}, x_{2}, \ldots, x_{n}\right] X(n−1)=[x0,x1,…,xn−1],X(n)=[x1,x2,…,xn],得到
X ( n ) = A X ( n − 1 ) A = X ( n ) X ( n − 1 ) † \begin{array}{l} X^{(n)}=A X^{(n-1)} \\ A=X^{(n)} X^{(n-1) \dagger} \end{array} X(n)=AX(n−1)A=X(n)X(n−1)†
可以通过状态的“轨迹数据” [ x 0 , x 1 , … , x n ] \left[x_{0}, x_{1}, \ldots, x_{n}\right] [x0,x1,…,xn]恢复出该系统。线性系统理论原动力系统的解形式为
x ( t ) = e K t x ( 0 ) = Φ e Λ t C x(t)=e^{K t} x(0)=\Phi e^{\Lambda t} C x(t)=eKtx(0)=ΦeΛtC
其中, C = Φ † x ( 0 ) C=\Phi^{\dagger} x(0) C=Φ†x(0)是基解矩阵的系统, Φ \Phi Φ和 e Λ t e^{\Lambda t} eΛt分别为 e K t e^{K t} eKt的特征值和特征向量。如果特征向量是实数,则对应的特征向量是指数级增长或是衰退的(取决于特征值的正负),如果特征值的虚部不为零,则存在震荡(更多细节请参考常微分方程的教材)。
同理,离散化后的动力系统的解也有类似的形式
x k = Ψ Λ k B x_{k}=\Psi \Lambda^{k} B xk=ΨΛkB
其中, B = Ψ † x 0 B=\Psi^{\dagger} x_{0} B=Ψ†x0是基解矩阵系数, Ψ \Psi Ψ和 Λ \Lambda Λ分别为矩阵 A A A的特征向量与特征值。
动态模态分解,其实就是给线性动力系统降维的一种方法。在很多应用中,数据的维度是非常高的(即 X X X矩阵是 K × N K\times N K×N的,而 K > > 1 K>>1 K>>1),所以计算 X ( n ) X ( n − 1 ) † X^{(n)} X^{(n-1) \dagger} X(n)X(n−1)†的特征值和特征向量就非常的困难。例如:气象海洋控制、飞行器对周围流体状态监测,脑神经科学中电位测量等等都需要安装大量的感知器。

这时,先对 X ( n − 1 ) X^{(n-1)} X(n−1)奇异值分解,并保留其前r阶( r ( < < K ) r(<
X ( n − 1 ) = U r Σ r V r † A ~ r = U r † A U r \begin{array}{c} X^{(n-1)}=U_{r} \Sigma_{r} V_{r}^{\dagger} \\ \tilde{A}_{r}=U_{r}^{\dagger} A U_{r} \end{array} X(n−1)=UrΣrVr†A~r=Ur†AUr
其中, A A A和 A ~ r \tilde{A}_{r} A~r是近似矩阵,前r个特征值和特征向量相同。不妨设 A ~ r = W Λ r W † \tilde{A}_{r}=W \Lambda_{r} W^{\dagger} A~r=WΛrW†,然后就可以根据 Λ r \Lambda_{r} Λr来对不同特征向量进行分类了。
总而言之,DMD,在系统是线性的假设下,我们就可以通过观测到的数据 [ x 0 , x 1 , … , x n ] \left[x_{0}, x_{1}, \ldots, x_{n}\right] [x0,x1,…,xn]来“恢复”该系统(也就是计算出矩阵 A A A )。根据线性系统理论,我们就可以通过计算 A A A的特征值特征向量知道不同空间上的“模态”在时间上“如何传递”(指数形增长、衰退或是震荡)。但是有些系统“状态维度‘较大,计算成本较高,我们可以通过先用“动态模态分解”的“小窍门“对其先降维,然后再去找特征值特征向量就简单得多了。
Procrustes problems
对于正交普鲁克问题,假设有两个测量值 X X X和 Y Y Y,目标是学习与数据测量相关的最佳正交变换。因此,A被约束为一个正交矩阵,最小化问题:
argmin A ∗ A = I ∥ Y − A X ∥ F \underset{\boldsymbol{A}^{*} \boldsymbol{A}=\boldsymbol{I}}{\operatorname{argmin}}\|\boldsymbol{Y}-\boldsymbol{A X}\|_{F} A∗A=Iargmin∥Y−AX∥F
上式的解为
A = U Y X V Y X ∗ \boldsymbol{A}=\boldsymbol{U}_{Y X} \boldsymbol{V}_{Y X}^{*} A=UYXVYX∗
其中, U Y X Σ Y X V Y X ∗ = Y X ∗ \boldsymbol{U}_{Y X} \boldsymbol{\Sigma}_{Y X} \boldsymbol{V}_{Y X}^{*}=\boldsymbol{Y} \boldsymbol{X}^{*} UYXΣYXVYX∗=YX∗是一个完全奇异值分解。或者, A = U P \boldsymbol{A}=\boldsymbol{U}_{P} A=UP,其中 U P H P = Y X ∗ \boldsymbol{U}_{P} \boldsymbol{H}_{P}=\boldsymbol{Y} \boldsymbol{X}^{*} UPHP=YX∗为极分解(KaTeX parse error: Expected '}', got 'EOF' at end of input: …oldsymbol{H}_{P为对称阵)。当 Y X \boldsymbol{Y X} YX满秩时,最小化问题有唯一解。
Physics-informed dynamic mode decomposition (piDMD)
ML实践者采取三种方法之一。
- 首先,观测偏差可以通过数据增强技术嵌入;然而,增强数据并不总是可用的,并且合并额外的训练样本可能会成为计算上的昂贵。
- 其次,可以通过适当地惩罚loss函数来包含物理约束。
- 第三,归纳偏差可以以数学约束的形式直接融入机器学习体系结构。
第三种方法可以说是 the most
principled 方法,因为它生成的模型严格满足物理约束。piDMD属于最后一类。
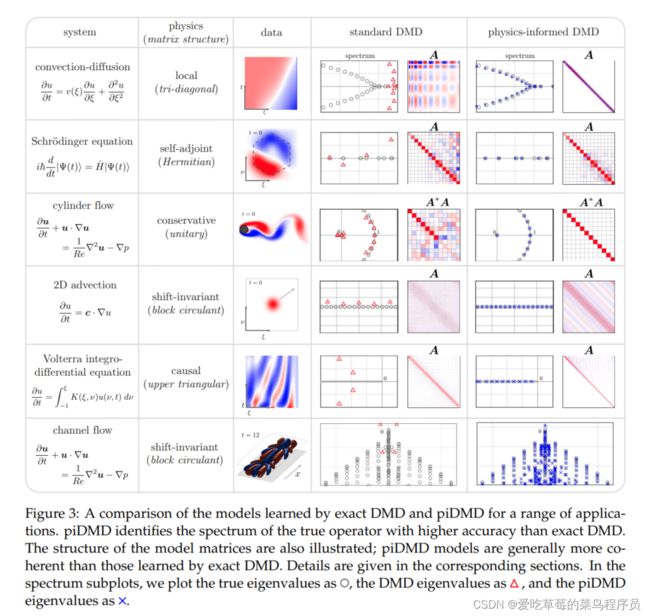
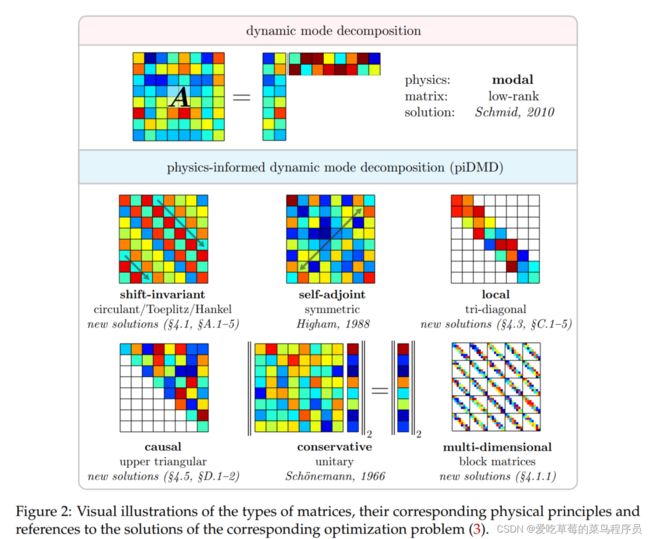
piDMD incorporates physical principles by constraining the matrix manifold of the DMD regression problem. We abandon the low-rank representation of A typically sought in model order reduction in favour of alternative or additional matrix structures more relevant to the physical problem at hand. In figure 2 we illustrate the matrix structures used in this paper, along with their corresponding physical principle and references for the optimal solutions.
piDMD framework requires four steps: modeling, interpretation,
optimization, and diagnostics:
- (1) Modeling Modeling Modeling Modeling: When studying a system from a data-driven perspective, it is common to have Modeling some partial knowledge of the underlying physics of the system. This first step in piDMD asks the user to summarise the known or suspected physical properties of the system at hand.(总结物理规律)
- (2)Interpretation: Having determined the physical principle we would like to enforce, we must translate these laws into the matrix manifold to which the linear model should be constrained. This step involves knowledge of the data collection procedure such as the spatial grid or the energy inner product.(物理规律转化为matrix manifold能被加入线性模型中)
- (3) Optimization: Equipped with a target matrix manifold, we may now solve the relevant Pro- Optimization problem (3). By suitably modifying the optimization routine, we can guarantee that
the resulting model satisfies the physical principle identified in step 1.(通过适当地修改优化程序,我们可以保证得到的模型满足第1步确定的物理原理) - (4)Diagnostics: Diagnostics: Diagnostics: Diagnostics: The final step of piDMD involves extracting physical information from the learned model A. For example, one may wish to analyse the spectrum or modes, compute the resolvent modes, perform predictions, or investigate other diagnostics.
如图1,通过增加shift-invariance物理信息到模型中。

这篇论文给出了不同类型的内嵌物理的矩阵流型,标准DMD利用A的低秩结构,有效地对学习到的模型进行诊断。我们所考虑的一些流形(如循环,三对角线,上三角形)没有明显的或有用的低秩近似。相反,这些矩阵通常有另一种结构,可用于执行快速诊断测试。例如,三对角矩阵很少有有意义的低秩近似,但仍然允许快速特征分解和奇异值分解。
Applying piDMD to enforce canonical physical structures
图3总结了一系列piDMD例子。The physical principles, corresponding matrix structures, and optimal solutions and extensions are summarised below:
- §4.1: Shift-invariant: Shift-invariant: Shift-invariant: Shift-invariant: circulant (and symmetric, skew-symmetric, or unitary, § Shift-invariant: A.1), low rank (§A.2),
non-equally spaced samples (§A.3), total least squares (§A.4), Toeplitz & Hankel (§A.5) - §4.2: Conservative: Conservative: Conservative: Conservative: unitary (§ Conservative: 2.2)
- §4.3: Self-adjoint: Self-adjoint: Self-adjoint: Self-adjoint: symmetric (§ Self-adjoint: 4.3), skew-symmetric (§B.1), symmetric in a subspace (§4.3.1)
- §4.4: Local: Local: Local: Local: tridiagonal (§ Local: 4.4), variable diagonals (§C.1), periodic (§C.2), symmetric tridiagonal
(§C.3), total least squares (§C.4), regularized locality (§C.5). - §4.5: Causal: Causal: Causal: Causal: upper triangular (§ Causal: D.1 D.2)
Shift-invariant systems(平移不变形)为例
移位不变性(也称为“平移不变性”)在物理科学中普遍存在。空间齐次系统-如常系数偏微分方程或卷积算子-是移动不变的,因此相对于任何(平稳的)观察者看起来是相同的。In view of
Noether’s theorem [69], the conserved quantity related to shift invariance is linear momentum; as such, incorporating shift invariance into a DMD model means that the model preserves linear momentum.
定义一个 S ϕ \mathcal{S}_{\phi} Sϕ算子,满足 S ϕ v ( ξ ) = v ( ξ + ϕ ) \mathcal{S}_{\phi} v(\xi)=v(\xi+\phi) Sϕv(ξ)=v(ξ+ϕ)对于所有的 v v v。我们说一个空间连续的线性算子 A A A是移位不变的,如果 A A A对所有移位 ϕ \phi ϕ都与 ϕ \phi ϕ-shift算子满足
S ϕ A = A S ϕ \mathcal{S}_{\phi} \mathcal{A}=\mathcal{A} \mathcal{S}_{\phi} SϕA=ASϕ
平移算子的一个应用表明,如果 A A A是平移不变量,那么对于所有 ξ \xi ξ值, e − λ ξ A e λ ξ \mathrm{e}^{-\lambda \xi} \mathcal{A} \mathrm{e}^{\lambda \xi} e−λξAeλξ值是常数。
假设我们正在研究一个周期域上的位移不变系统。 我们从连续公式到离散空间,并假设函数表示为 u ( ξ , t ) u(\xi, t) u(ξ,t)。 能够得到在 ξ = [ − 1 , − 1 + Δ ξ , … , 1 − Δ ξ ] \boldsymbol{\xi}=[-1,-1+\Delta \xi, \ldots, 1-\Delta \xi] ξ=[−1,−1+Δξ,…,1−Δξ]的空间样本。discrete-space linear operator A A A可以表示为
A = F diag ( a ^ ) F − 1 ( 15 ) \boldsymbol{A}=\mathcal{F} \operatorname{diag}(\hat{\boldsymbol{a}}) \mathcal{F}^{-1}(15) A=Fdiag(a^)F−1(15)
其中, F j , k = e 2 π i ( j − 1 ) ( k − 1 ) / n / n \mathcal{F}_{j, k}=\mathrm{e}^{2 \pi \mathrm{i}(j-1)(k-1) / n} / \sqrt{n} Fj,k=e2πi(j−1)(k−1)/n/n以及 F − 1 = F ∗ \mathcal{F}^{-1}=\mathcal{F}^{*} F−1=F∗, a i ^ \hat{a_{i}} ai^为未知的特征值,上式可以写为
A = [ a 0 a n − 1 … a 1 a 1 a 0 ⋱ ⋮ ⋮ ⋱ ⋱ a n − 1 a n − 1 … a 1 a 0 ] \boldsymbol{A}=\left[\begin{array}{cccc} a_{0} & a_{n-1} & \ldots & a_{1} \\ a_{1} & a_{0} & \ddots & \vdots \\ \vdots & \ddots & \ddots & a_{n-1} \\ a_{n-1} & \ldots & a_{1} & a_{0} \end{array}\right] A=⎣⎢⎢⎢⎢⎡a0a1⋮an−1an−1a0⋱……⋱⋱a1a1⋮an−1a0⎦⎥⎥⎥⎥⎤
将式(15)带入
piDMD regression: argmin A ∈ M ∥ Y − A X ∥ F \text { piDMD regression: } \quad \underset{A \in \mathcal{M}}{\operatorname{argmin}}\|\boldsymbol{Y}-\boldsymbol{A} \boldsymbol{X}\|_{F} piDMD regression: A∈Margmin∥Y−AX∥F
得到
argmin a ^ ∥ diag ( a ^ ) X − Y ∥ F \underset{\hat{a}}{\operatorname{argmin}}\|\operatorname{diag}(\hat{\boldsymbol{a}}) \mathcal{X}-\mathcal{Y}\|_{F} a^argmin∥diag(a^)X−Y∥F
其中, X = F ∗ X and Y = F ∗ Y \mathcal{X}=\mathcal{F}^{*} \boldsymbol{X} \text { and } \mathcal{Y}=\mathcal{F}^{*} \boldsymbol{Y} X=F∗X and Y=F∗Y分别为 X X X和 Y Y Y的空间离散傅里叶变换。上式的行解耦产生n个最小化问题
argmin a ^ j ∥ a ^ j X ~ j − Y ~ j ∥ F for 1 ≤ j ≤ n \underset{\hat{a}_{j}}{\operatorname{argmin}}\left\|\hat{a}_{j} \tilde{\mathcal{X}}_{j}-\tilde{\mathcal{Y}}_{j}\right\|_{F} \quad \text { for } 1 \leq j \leq n a^jargmin∥∥∥a^jX~j−Y~j∥∥∥F for 1≤j≤n
其中,每个特征值的解满足
a ^ j = Y ~ j X ~ j † = Y ~ j X ~ j ∗ / ∥ X ~ j ∥ 2 2 \hat{a}_{j}=\tilde{\mathcal{Y}}_{j} \tilde{\mathcal{X}}_{j}^{\dagger}=\tilde{\mathcal{Y}}_{j} \tilde{\mathcal{X}}_{j}^{*} /\left\|\tilde{\mathcal{X}}_{j}\right\|_{2}^{2} a^j=Y~jX~j†=Y~jX~j∗/∥∥∥X~j∥∥∥22
Experiment
疑问:
奇异值分解找特征值和特征向量比直接求逆快吗?
答:
奇异值分解求特征值和特征向量计算很快
文献参考
https://zhuanlan.zhihu.com/p/39304706