【C++语言实现】【算法分析与设计】全排列问题

全排列问题

设A={a1,a2,…,an}是要进行排列的n个元素的集合
这里用技巧性算法，即观察
当n=1时，输出a1
当n=2时，输出a1a2,a2a1
当n=3时，输出：

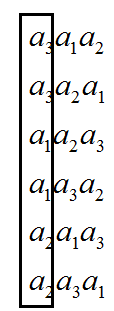
我们注意观察，每种可能的排列的第一个元素，我们发现第一个元素的值只能是n=3时，出现的所有可能的元素，而后面则是另外剩下的3-1=2个数的全排列，而这另外剩下的3-1=2个数的全排列恰好就是n=2时的操作步骤，也就是说，先确定首元素，其余元素执行上一步的全排列，这样不断地执行上一步的上一步……就达到了递归的效果，即有了这样一个函数：
range(A) = a1range(A1), a2range(A2),…, anrange(An)
这个算法的C++实现如下（By 漫天风沙里的人）：

C++实现代码

#include 
using namespace std;
//例：递归与排列问题
void printResult(char A[],int n)
//用于打印排列结果的函数
{
    for(int i = 0;i< n;i++)
    {
        cout<<A[i];
    }
    cout<<endl;
}
void range(char A[],int k,int n)
//A字符数字代表要排序的序列
//k是从哪里开始排列，n是数组有多少个元素
//这里k和n减去1是为了让这个数组贴合题目要求下标从1开始
{
    char temp;//用于保存for循环中交换数据的临时变量
    if(k-1 == n-1)//如果数组就1个元素就无需排列直接输出
    {
        printResult(A,n);
    }
    else
    {
        for(int i = k-1;i < n;i++)//换一下位置确定首元素
        {
            //这里为什么提前交换首元素
            //为什么不直接从第一个开始直接递归
            //答：直接递归按代码顺序执行只能无限递归下去，永远是第一次的首元素
            //这样就毫无意义，不如先交换，第一种类的首元素怎么交换还是它
            //第二种类开始才正式有交换效果
            temp = A[k-1];
            A[k-1] = A[i];
            A[i] = temp;
            range(A,k+1,n);//递归调用排列剩下两个元素
            //换下一个首元素
            temp = A[k-1];
            A[k-1] = A[i];
            A[i] = temp;
            //换回原始状态
        }
    }
}
int main()
{
    char A[]={'A','B','C','D'};
    range(A,1,4);
    return 0;
}

解释其递归的原理（以四个元素为例）

【注意】有关循环中两次交换和一次递归调用函数的解释：
（我们假设排序这个字符数组char A[] = {‘A’,’B’,’C’,’D’}，对其进行全排列）首先判断，第一次交换其实并不是真正的交换，我们可以看到

//第二种类开始才正式有交换效果
            temp = A[k-1];
            A[k-1] = A[i];
            A[i] = temp;

这里仅仅是为了选择首元素进行全排列，让A[k]和A[i]的值进行交换，这句话的通俗解释如下：
比如有四个字母ABCD进行全排列，那么根据刚才的算法，我们应该选择首元素，然后让首元素后面的元素进行全排列，那么接下来进行第一次交换，第一次交换时，我们知道k=1（k-1=0，这里为了让大家能通俗的理解，C++数组下标默认从0开始，我取k-1后就可以理解为从1开始了），A[k]目前是’A’，很凑巧A[i]也是’A’，这就确定了首元素是A，然后确定首元素后就知道首元素后面的其他元素都是什么，对后面的元素进行全排列，即目前：

执行后三个问号是BCD进行全排列，那么BCD全排列还需要确定其首元素，接下来就执行递归操作：

 range(A,k+1,n);//递归调用排列剩下两个元素

递归时先判断一下k和n的值，我们知道，k已经在执行语句时增加了1即现在k是2，而n还是4，这个时候进入递归，我们再执行一遍刚才的交换，此时A[k]是’B’，A[i]是’B’，这就进入到了B为首元素的，剩下两个元素的全排列，即：

然后又进入递归：

 range(A,k+1,n);//递归调用排列剩下两个元素

执行后k变成了3，n还是4，继续，不符合if的条件，继续进入循环，此时A[k]是’C’，A[i]是’C’，此时就进入到了C为首元素，剩下一个元素的全排列，一个元素只有一种排法，当然现在我们只看说C首元素，即：

 range(A,k+1,n);//递归调用排列剩下两个元素

执行后k=4,n=4,符合了if条件，开始打印，即打印了四个元素全排列的第一个结果：

然后打印后，没了if条件没了其他代码，则应该是退出range函数，我们需要注意此时已经执行了三层的递归函数range，这三层分别是：

• K=1,n=4
• K=2,n=4
• K=3,n=4

【注意：为什么没有k=4,n=4呢，因为那个时候符合了if条件，而if条件中并没有执行递归的代码，而是打印并结束函数】
则退回倒数第二层的递归时，退回到上一层k=3,n=4的时候，然后接下来继续执行for循环的下一半即

这个时候做了个交换，这个交换的意思是，首元素由k=3,n=4时的C换成了D，即此时变成了如下情况：

然后注意，我们现在在else条件的循环体里，这时执行完了倒数第二层的else条件的循环体中的第一层循环，我们知道此时循环是从k到n的即3到4的，刚执行的第一次是k=3，接下来执行第二次i=4时（注意只是i增加，k并没有增加还是3）的循环，由于此时k=3，A[k]是’C’（再次提醒我们这里的数组是下标从1开始），i也是4，A[i]是’D’，这次做了一次真正的交换，A[k]变成了’D’，A[i]变成了’C’，即原字符数组A[]={‘A’,’B’,’D’,’C’}，然后执行了到了下一步递归：
range(A,k+1,n);//递归调用排列剩下两个元素
执行后k=4,n=4,符合if条件，开始打印，得到了四个元素全排列的第二个结果即：

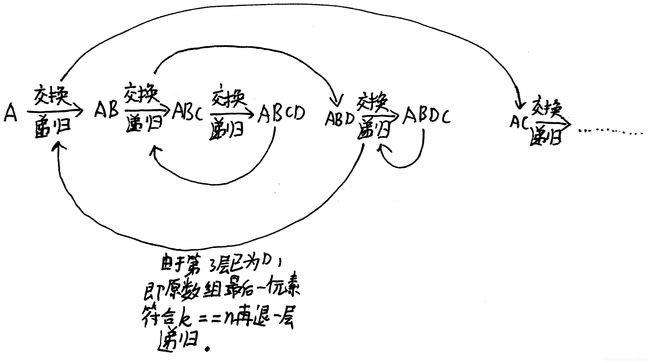
接下来无限地重复上述过程……那么总结起来大概是这样的步骤图（博主字太烂，见谅）【注意：k-1等于n-1相当于k等于n，这么写是为了时刻提醒大家这里是以下标1开头的数组做说明】：

有关其时间复杂度

（*：下面是纯数学方面的讨论）我们来研究一下这个算法的时间复杂度：
由于其是全排列算法，则其算法的最坏时间渐近函数的上界大O，即为：

其实根据《算法导论》中的斯特林公式还可以继续展开算，但是笔者就不算了……太难了，这里给出斯特林公式：

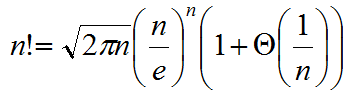
就当它是O(n!)吧，其实严格地讲，我们很容易就直接求出它的递归方程的通解H(n)=n!，那它的时间复杂度应该是严格的Θ(n!)，符合大Θ标记的定义（有关此定义请参考《算法导论（第三版）》的中文译本的26-28页的全部知识），大的函数图像是这样的：

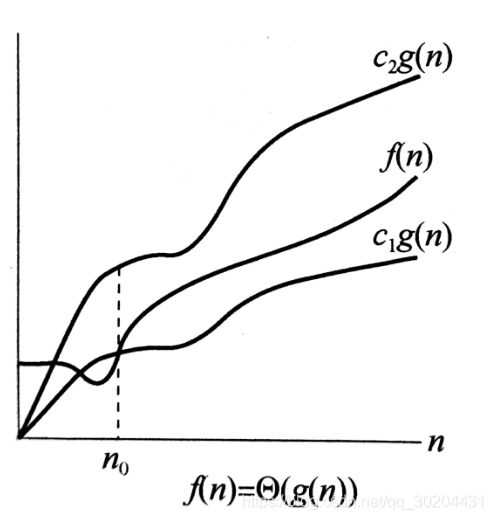
博主个人理解为这时本算法的函数图像应该是一个飞快增长，且两个上下紧界就是的函数h(n)（阶乘函数取定义域大于等于0的部分，因为这时实际性的问题，所以要根据实际意义求出定义域），大致画一下是这样（不知道对不对，如果不对请大佬在评论区指出来）：

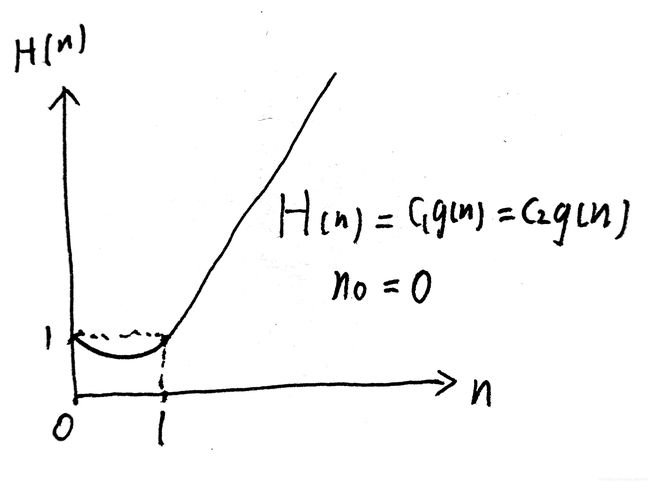
反正这时间复杂度挺糟糕的……