【统计学】贝叶斯推理方法
贝叶斯推理方法
随着因特网的普及和同步技术的发展, 贝叶斯统计开始运用于商业领域。 通过互联网可以实现自动收集顾客的购买和检索记录, 从而推测顾客的类别。 在这一点上, 贝叶斯统计学完胜传统意义上的统计学。如今, 许多互联网企业都在实际应用贝叶斯统计。 其中, 微软由于很早就开始在商业活动中运用贝叶斯统计学而闻名。
Windows的操作系统帮助功能中就导入了贝叶斯统计。 此外, 在网上搜索“小孩病症”的时候, 优先显示可靠结果的软件也已经开发出来。 微软的前董事长比尔・盖茨在1996年曾在报纸内容中称, 微软之所以在激烈的市场竞争中胜出, 正是由于采用了贝叶斯统计。 比尔・盖茨还在2001年关于基本方针的演讲中称, 微软的21世纪战略正是贝叶斯统计战略, 公开表示, 已经在全世界范围内挖到了许多贝叶斯统计研究人才。 该发言引起了很大关注。
谷歌搜索引擎的自动翻译系统中也引入了贝叶斯统计技术。
当然, 贝叶斯统计技术在IT企业之外的各个领域也有着广泛应用。例如, 消除传真图像中的杂音就运用了贝叶斯统计技术。 此外, 医疗领域的“自动诊断系统”等也需要用到贝叶斯统计。贝叶斯统计的优势在于, “在数据少的情况下也可以进行推测, 数据越多, 推测结果越准确”, 以及“对所获的信息可做出瞬时反应, 自动升级推测”的学习功能。 了解了这一点之后, 就完全可以理解为什么贝叶斯统计是非常适合应用于高端商业的技术了。
信息增加导致概率变化 “贝叶斯推理”的基本方法
1-1 通过贝叶斯推理来辨别“买东西的人”和“随便逛逛的人”
本讲将通过一个商业案例, 为大家介绍经典的贝叶斯推理方法。商店里的售货员最关心的问题莫过于“这位顾客究竟是来买东西的, 还是随便逛逛而已”。 真正来买东西的顾客, 一般而言, 比起四处逛逛看看, 更倾向于在最短时间内找到自己需要的商品。 另一类顾客则是这样的: 一时不急着买, 而是先随便问问价格, 为以后购买做个参考。 对待前者, 作为售货员, 理应为其介绍需要的商品并让其买下; 而对待后者, 如果同样花费时间为其推荐商品, 顾客不但不会购买, 反而会感到厌烦, 结果适得其反。
所以对于店员来说, 通过顾客的行为来揣测他们的真实想法, 是一项重要的本领。 很多店员可以做到: 通过直觉来判断顾客属于哪一类,而这正是身为一名店员的重要工作技巧。 在此, 我们将这种“基于直觉的判断”数值化, 从而使它可以通过计算获得。 把方法编成手册, 教给新店员, 这就像在互联网上能够实现自动判断的AI(人工智能) 一样,是一项意义非凡的工作。
下文将具体介绍“将店员的判断方法数值化”的方法, 该方法恰巧适用贝叶斯统计学。 进而言之, 通过该事例, 我们也可以弄懂贝叶斯统计学的概念。 下文将分节进行解说。
1-2 第一步: 通过经验设定“先验概率”
假设一个场景: 面前有一位顾客, 此时你需要做的是, 推测该顾客究竟是“来买东西的人”, 还是“随便逛逛的人”。 只有做出正确的判断,才能采取正确的接待方法。
推算的第一步:将两种顾客(来买东西的顾客、随便逛逛的顾客)的比例进行数值分配。这句话的意思是:假设面前的这位顾客一定属于两种中的一种,以此为前提,该顾客为第一种或第二种的可能性分别为多少?将这个可能性用数值表示出来。
在贝叶斯统计学中,这种“某种类别的概率(比例)”有一个专有名词,叫作“先验概率”。“事前”的含义是:在获得某项信息之前。此处的“信息”是指:附加的状况,比如顾客忽然过来询问。通过“过来询问”这一信息,可以对顾客类别的推算进行修改,而“先验概率”是指,在“过来询问”或“不过来询问”的情况发生之前进行的概率判断。
通常,“先验概率”可通过经验来判断。在特殊情况下,即使没有类似经验,也可以进行判断,这部分特殊事例将在第3讲进行解说,此处暂且不做讨论。根据自己的经验,每5位顾客中就有1位是“来买东西的”,也就是说,这一部分顾客占全体的20%(0.2),那么剩下“随便逛逛”部分的比例便为80%(0.8)。这两个数字,便是两类顾客的“先验概率”。
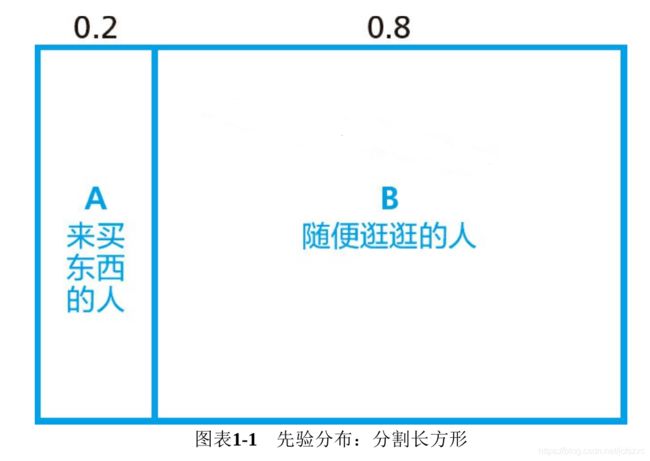
在这个事例中,在观察面前顾客的行为之前,判断“该顾客是属于概率0.2的买东西的人,还是概率0.8的随便逛逛的人”,这个过程被称为“某一类别的先验分布”,如图表1-1所示。
图表1-1中的大长方形被分割为两部分,两部分的面积所占比例分别为0.2和0.8,这正是分割时的诀窍。本书将在后面逐渐阐明:“面积”的概念在贝叶斯概率的计算中,起着重要的作用。以上图示的方法为本书独创。希望各位读者将这幅图牢记于心,这样有助于在头脑中勾勒出贝叶斯统计学方法的大致雏形。
该图可以理解为:将整体分为两种不同的情况。这意味着,自己所处的环境为A或B中的一个,A情况下的顾客为“来买东西的人”,B情况下的顾客为“随便逛逛的人”,但不知道究竟是A还是B。只是先在头脑中构筑一个大致的印象。哲学上将这种见解称为“可能世界”,在进行逻辑推算或概率推算时,采用这种“划分互不相同的可能性”的思维方法,有利于整理思路。
在这里将长方形的面积设定为0.1和0.4,两部分的比例依然为1:4,这与设定为0.2和0.8时的比例相同。那么,为何要将面积设置为0.2和0.8呢?这是因为,用数值来计算概率的情况下,需要在多种可能性中,选取“将各部分概率相加,总和为1”的那一种,这种情况被称为“标准化条件”。
1-3 第二步:设置发生“向店员询问”事件的条件概率
在这一步,我们要做的是:为“来买东西的人”和“随便逛逛的人”这两类顾客分别设定“向店员询问”的概率。如果没有相关经验和数据作为支撑,这项工作是无法完成的。上一节讲到,即使没有相关经验,也可以设定先验概率。但此处的“各个分类的行动概率”,必须是基于一定的经验、实证、实验的数值。
图表1-2中的数值,是为了计算简便而设定的,并非真实数据。
从图表1-2中可以看出,“来买东西的”顾客向店员询问的概率是0.9,而“随便逛逛的”顾客向店员询问的概率只有0.3。
需要注意的是:图表1-2从横向来看,0.9+0.1=1,0.3+0.7=1,两行都满足标准化条件;而纵向来看,0.9+0.3≠1,也就是说并不满足标准化条件。具体分析一下:横向的一行,表示某一类别的顾客可能采取的两种行动。比如第一行数字,表示“来买东西的人”向店员“询问”或“不询问”这两种行为,顾客有可能询问,也有可能不询问,最终采取的行动一定是其中之一,没有第三种可能性。而纵向来看,第一列数字表示,“来买东西的人”向店员询问的概率为0.9,“随便逛逛的人”向店员询问的概率为0.3,两个数字相加之和并不等于1。这是因为,对象范围包含了两个不同类别的顾客,并且也没有涵盖所有的行动。
图表1-2中的数字,表示“某一特定类别采取各种行动的概率”,这在高等数学中被称为“条件概率”。用“原因”的概念来解释,即“在原因明确的情况下,某一类别采取各项行动的结果概率”(第15讲中将介绍:如何用符号来表示条件概率)。
将两个类别的顾客,进一步按照“询问”和“不询问”的条件来分类,那么前文所述的两个大类别又可以细分为四个小类别,分别是:“来买东西的人询问店员”“随便逛逛的人询问店员”“来买东西的人不询问店员”“随便逛逛的人不询问店员”,如图表1-3所示
一共存在四种可能性:来买东西的人询问店员(左上区域)、来买东西的人不询问店员(左下区域)、随便逛逛的人询问店员(右上区域)、随便逛逛的人不询问店员(右下区域)。概率的具体计算方法将在第10讲中具体介绍,此处对于结论先进行说明:各个区域所表示的概率与每个长方形的面积相等。长方形的面积可以用乘法求得,如图表1-4所示。
下面我们来确认一下,这四个“可能世界”(所有可能发生的情况)的概率之和:
0.2 × 0.9 = 0.18 0.2 × 0.1 = 0.02 0.8 × 0.3 = 0.24 0.8 × 0.7 = 0.56 ( 0.18 + 0.02 ) + ( 0.24 + 0.56 ) = 1 0.2×0.9=0.18 0.2×0.1=0.02\\ 0.8×0.3=0.24 0.8×0.7=0.56\\ (0.18+0.02)+(0.24+0.56)=1 0.2×0.9=0.18 0.2×0.1=0.020.8×0.3=0.24 0.8×0.7=0.56(0.18+0.02)+(0.24+0.56)=1
1-4 第三步:通过观察到的行为,排除“不可能的情况”
下面,让我们进一步进行推测。
作为一名店员,现在你面临的情况是:顾客上前来打招呼。这也意味着,你观察到了顾客的某一种行为。这为“可能世界”又增添了一条信息。
这条信息的内容是:“不询问店员”的可能性消失了。上一节中提到,在顾客类别包括“来买东西的人”和“随便逛逛的人”两类,顾客的行为包括“询问”和“不询问”两类的情况下,“可能世界”共分为4种。在现实世界中,因为已经观察到了“询问”这一行为,因此“不询问”这一行为覆盖的世界就不复存在了。这意味着,“可能世界”受到了限制。下面我们借助图形来理解这一问题。(图表1-5)
因为“可能世界”变成了2个,从而我们可以推测获得新的数值。
在一部分可能性不复存在,而一部分可能性又在现实中受到了限制的情况下,会发生些什么呢?这正是所谓的——在推测中“概率发生变化”。下面通过一个简单的例子,来解释一下何为“概率的变化”。
现在,有人洗好了52张扑克牌摆在你面前,扑克牌背面朝上。当被问道“最上面一张扑克牌的花色是什么呢?”的问题时,如果你回答“是黑桃”的话,那么,这一推测为正确的概率是多少呢?当然,是四分之一,对吧。因为扑克牌共有四种花色,每一种花色的可能性都是相等的。
但是,如果对方背着你偷看了最上面的一张扑克牌,并告诉你“最上面一张扑克牌其实是黑色的”,结果又会怎样呢?从你的推测来看,扑克牌是红色花色的可能性自然就不存在了。当然,你的推测也可能会发生变化吧。也就是说,此时只有可能是黑桃或梅花,所以,你推测这张扑克牌的花色“是黑桃”的概率应当为二分之一。
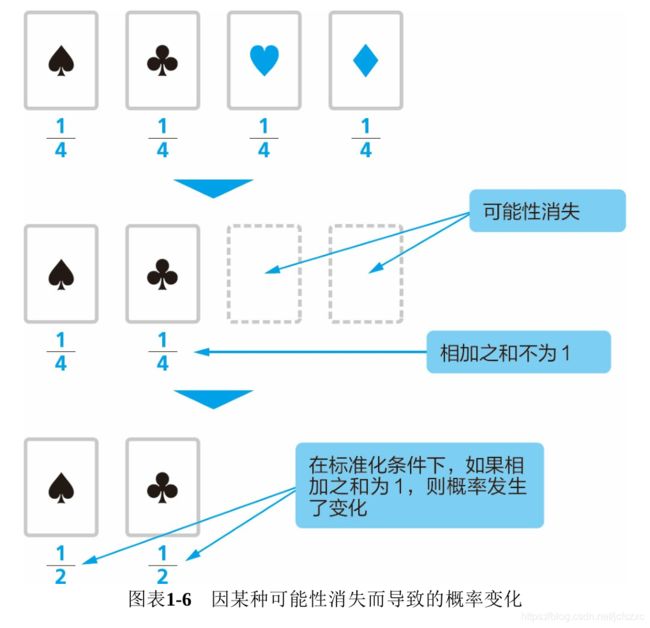
将这个实验的来龙去脉用图来表示,如图表1-6所示。
最初,4种花色的概率相加之和为1。但是,由于红色花色的可能性不复存在,此时黑桃的概率和梅花的概率相加之和便不等于1。为此,还是要保持之前的比例关系,通过恢复标准化条件(使所有情况的概率相加之和为1),所以,花色为黑桃的概率应变更为二分之一。
1-5 第四步:寻求“来买东西的人”的“贝叶斯逆概率”
上一节,由于观察到“询问”这一行动,使得“可能世界”被限定在两个以内。也就是说,面前的顾客所属的世界,要么是“来买东西的人询问店员”,要么是“随便逛逛的人询问店员”,只有这两种可能性。显示其可能性的数值(概率),如图表1-7所示。
根据观察到的行为,可能性被限定为两种,此时,所有情况的概率(长方形面积)之和已经不为1。因此,要采取上一节中用扑克牌举例的办法,保持比例关系,恢复标准化条件,从而使概率发生变化。具体如下所示:
(左边长方形的面积):(右边长方形的面积)=0.18:0.24=3:4
简化比值,合计3+4=7,如果按照除法计算,就会得出“相加得1”的结果。也就是说,
(左边长方形的面积):(右边长方形的面积)=3:4=3/7:4/7
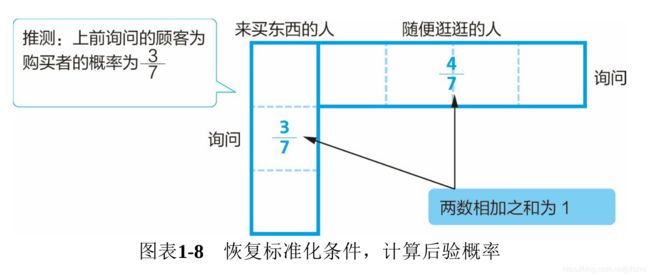
用图表示,如图表1-8所示。
从上表中我们可以看出,上前询问的顾客为购买者的概率,可以推定为3/7。这个概率,被称为“贝叶斯逆概率”或“后验概率”。
在此,对“逆概率”一词中的“逆”的含义,进行简要说明。(在之后的讲义中会逐渐进行详细说明)。
所谓的“逆”是指:用与之前相反的方法,来解析表示几个互不相同的“世界”的图形。截至上一节的观点是:顾客共分两种类别,每一种类别都会随机做出“询问”或“不询问”的行为,这一观点的前提是对图表进行纵向观察。这正是从“类别”这一原因,得到“行动”这一结果的处理方法。但是,现在让我们来横向观察图表。也就是说,“上前询问”的顾客可分为“来买东西的人”和“随便逛逛的人”两种类别,从中随机选择一种。从“询问”这一行动的结果追溯到“类别”这一原因。【结果→原因】这一过程,就是“逆概率”这一概念中“逆”的含义。
1-6 贝叶斯推理过程的总结
用图表对于之前提到的后验概率的计算方法进行总结,如图表1-9所示。
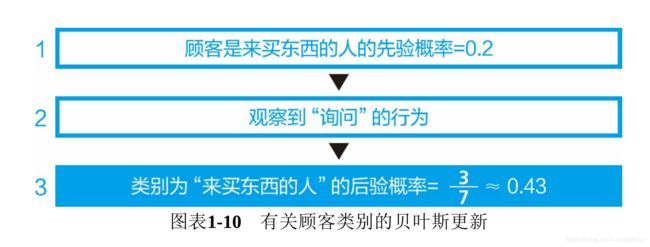
那么,通过求后验概率,我们能够了解到什么呢?其实,只要抽出图表的开头、中间和结尾部分,并填入数值,结果就很明确了。(图表1-10)
看这个图表便可了解到,在没有观察到任何行为时,面前的顾客是“来买东西的人”的概率为0.2(先验概率),但观察到“上前询问”这一行为之后,数值便更新为约0.43(后验概率)。也就是说,虽然并不能断定这位顾客就是“来买东西的人”,但这一结果的可能性提高到了以前的两倍,这便是“贝叶斯更新”。
在本书中,上述过程称为“贝叶斯推理”。贝叶斯推理可以总结为:通过观察行动(信息),将先验概率通过贝叶斯更新,转换为后验概率。在本书中,每个案例中进行的推算称为“贝叶斯推理”,而将这些案例中的推算方法整合起来,便是“贝叶斯统计学”。
小结:
- 设定两个类别(“来买东西的人”和“随便逛逛的人”)的概率(先验概率)。
- 设定类别“来买东西的人”“上前询问”以及“不上前询问”两种行为的概率,和“随便逛逛的人”“上前询问”以及“不上前询问”的概率(条件概率)。这需要一定的经验和数据作为支撑。
- 因为观察到了“上前询问”的行为,因此,可以排除掉“不上前询问”的可能性。
- 使“来买东西的人上前询问”的概率和“随便逛逛的人上前询问”的概率组合,满足标准化条件。也就是说,在保持比例关系的前提下,使其相加之和等于1。
- 还原标准化条件后的“来买东西的人”的概率,也就是观察到“上前询问”行为后,判断“来买东西的人”类别的后
验概率。
问”以及“不上前询问”两种行为的概率,和“随便逛逛的人”“上前询问”以及“不上前询问”的概率(条件概率)。这需要一定的经验和数据作为支撑。 - 因为观察到了“上前询问”的行为,因此,可以排除掉“不上前询问”的可能性。
- 使“来买东西的人上前询问”的概率和“随便逛逛的人上前询问”的概率组合,满足标准化条件。也就是说,在保持比例关系的前提下,使其相加之和等于1。
- 还原标准化条件后的“来买东西的人”的概率,也就是观察到“上前询问”行为后,判断“来买东西的人”类别的后
验概率。 - 根据观察到的行为,先验概率更新为后验概率。这就是贝叶斯更新。