面向初学者的蒙特卡洛树搜索MCTS详解及其实现

目录

 

0. 序言

1. 蒙特卡洛算法的前身今世

2. 蒙特卡洛搜索算法的原理

2.1 Exploration and Exploitation（探索与利用）

2.2 Upper Confidence Bounds（UCB）

2.3 蒙特卡罗搜索的基本操作

2.3.1 选择

2.3.2 扩展

2.3.3 模拟

2.3.4 反向传播

2.4 蒙特卡洛搜索算法的流程图

3. 蒙特卡洛搜索算法示例

4. 蒙特卡洛搜索树算法的实现

4.1 TreeNode树节点类

4.2 选择

4.3 扩展

4.4 模拟

4.5 反向传播

5. 基于蒙特卡洛搜索算法的五子棋示例

6. 参考

 

---

0. 序言

相信许多人和我一样，对人工智能的认识始于2016年，Deepmind推出的AlphaGo与围棋大师李世石的惊世一战，让“人工智能”这个名词，被千家万户所熟知。尽管深度神经网络早在很多年前凭借其在图像识别等方面一骑绝尘的表现成为科研机构研究的热点，自此之后，人工智能才变成了一股时代的浪潮，浩浩荡荡裹挟着我们向着陌生未知的领域奔涌而去。

最近一直在做棋类博弈相关方面的探究，各种算法千变万化，都离不开对蒙特卡洛搜索算法（Monte Carlo Tree Search）这一经典搜索算法的使用，本文将以讲清基本的蒙特卡洛搜索算法（后文简称为MCTS）为目的，介绍这一算法涉及的方方面面的知识点，力求让读者以及自己能彻底琢磨透这一算法。

1. 蒙特卡洛算法的前身今世

人们对游戏AI的探索始于完美信息博弈游戏（perfect information games），这类游戏的特点就是游戏参与者没有隐藏的信息（例如英雄联盟等moba类游戏的战争迷雾），也没有任何不确定因素（比如玩大富翁的时候要掷色子）。这类游戏显然是最好研究的（像星际争霸这样的游戏AI至今还没有战胜人类）。因为在游戏中的每一步都是确定的，所以理论上，我们是可以穷举所有的情况从而构建一颗“游戏树”（如下图井字棋的游戏树），我们可以按照依次取最大值最小值的原则不断向下搜索（因为敌我双方的目的是相反的），这种方法就叫做Minmax方法。

然而，这种方法要求我们要穷举所有可能的情况，这在绝大多数的游戏中显然是不现实的，因此人们又想到寻求一个函数对当前局面进行判断，在树扩展的过程中及时对这棵树进行剪枝，这种方法在国际象棋这个领域取得了一定成果，但是对大部分游戏，依然不行。

而在此类领域，MCTS体现其强大的能力。我们想象，有两个对围棋一无所知的人，小明和小白，他们虽然不知道怎么下才能赢，但是他们依然遵守规则坚持不懈的下棋。经过一番激烈的菜鸡互啄，小明最终赢了小白，这个时候小明对围棋的认识加深了一步——“原来第一步要下天元才能赢啊！”（这不正确！），小白对围棋的认识也加深了一步——“第一步下在棋盘边缘上会输啊！”，小明和小白继续下棋，下到天荒地老，他们二人对围棋的认识都在不断加深，好多好多年过去了，小明赢了6000盘，小白赢了4000盘，那么我们就可以认为，在这种情况下小明胜率60%，小白胜率40%。这个例子告诉我们什么呢？大力出奇迹啊！通过大量的模拟，我们可以提高对某一种事物的认识，并对当前局面有一个更好的估计，这就是MCTS的基本思想，下面我们对其原理和步骤进行进一步介绍。

2. 蒙特卡洛搜索算法的原理

2.1 Exploration and Exploitation（探索与利用）

在具体讲MCTS之前，我们首先介绍Exploration and Exploitation，这个在强化学习经常遇到的一个困境和难题。回到我们上面提到的小明和小白下围棋的例子，什么是“Exploration”？探索就是向未知的领域勇敢的进发。如果小明不尝试新的招法，他永远不会发现，开局最好的下法不是下天元，是四个角星位附近。什么是“Exploitation”？利用就是经验万岁。经验有时候虽然不靠谱，但大多数时候还是管用的，而且你下的越多，你的经验就越靠谱。探索也好，利用也罢，怎么去确定他们的分配比例呢？这就是难题所在了，我们可以设置一个概率参数p，以p的概率探索，以1-p的概率利用。还有很多种方法，我们下面要介绍的UCB也是其中的一种。

2.2 Upper Confidence Bounds（UCB）

在本文中，我们采用UCB方法来确定何时进行探索和利用。公式如下：

其中 v_i 是节点估计的值（比如胜率），n_i 是节点被访问的次数，而 N 则是其父节点已经被访问的总次数。C 是可调整参数。（引用自蒙特卡洛搜索MCTS）

前者代表我们的经验，而后者代表我们的勇气。我们重点看一下我们的“勇气”。后面的值越大，代表着相对父节点的访问，我们访问当前这个子节点的次数偏少，因此我们要多多关注它，反之，则正好相反。

2.3 蒙特卡罗搜索的基本操作

 

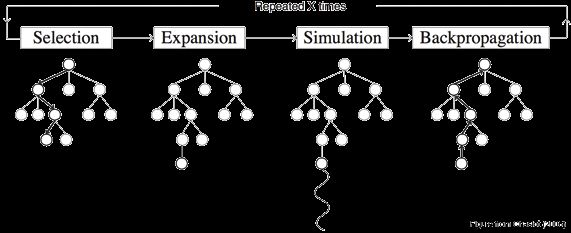
算法的每次迭代分为四步——选择，扩展，模拟和反向传播。我们先简单介绍一下这四步，后文我们会给一个详细迭代的例子。

2.3.1 选择

基于2.2中的选择算法，从根节点开始，我们选择采用UCB计算得到的最大的值的孩子节点，如此向下搜索，直到我们来到树的底部的叶子节点（没有孩子节点的节点），等待下一步操作。

2.3.2 扩展

到达叶子节点后，如果还没有到达终止状态（比如五子棋的五子连星），那么我们就要对这个节点进行扩展，扩展出一个或多个节点（也就是进行一个可能的action然后进入下一个状态）。

2.3.3 模拟

之后，我们基于目前的这个状态，根据某一种策略（例如random policy）进行模拟，直到游戏结束为止，产生结果，比如胜利或者失败。

2.3.4 反向传播

根据模拟的结果，我们要自底向上，反向更新所有节点的信息，具体更新哪些信息在后面示例和实现中会讲。

2.4 蒙特卡洛搜索算法的流程图

具体的解析在第三节会讲。

3. 蒙特卡洛搜索算法示例

如果只看上面的解析，可能会因为语言不准确等原因，产生许多误解，因此首先先放上一个标准算法，然后再实际操作一个例子。

下面我将用一个例子，去讲解蒙特卡洛算法的实现。

第一次迭代：

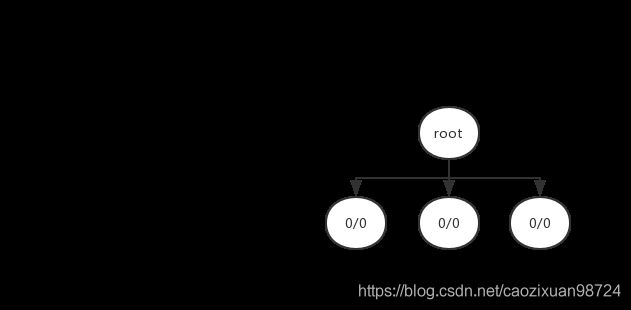
1. 扩展：没有可以选择的节点，因此我们要进行扩展。我们假设从根节点一共有三个可选的动作，一共可以扩展出三个可选的节点。

2. 选择：此时对于这三个节点，其值均为0/0（即访问次数为0，胜利次数也为0），带入公式，其UCB值均为正无穷。我们就选择第一个节点。

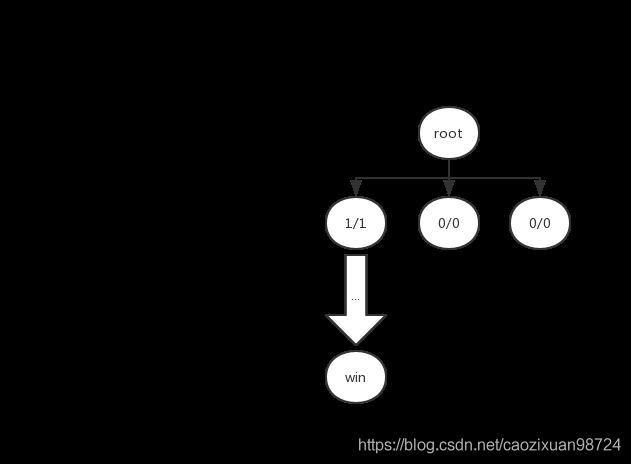
3. 模拟：从当前选择的节点开始，根据一定的policy function进行模拟，直到到达terminal state。policy function在后面实现过程中会细讲。我们假设这次模拟的结果是胜利。

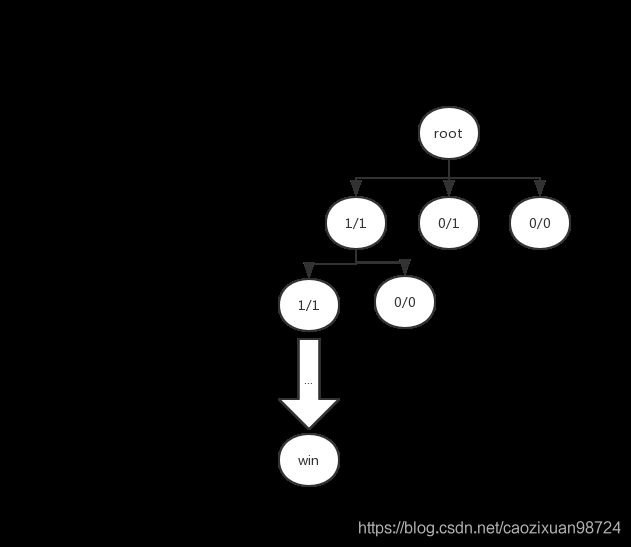
4. 反向传播：将选择的节点的值更新为1/1，如下图所示。因为没有相应的父节点，因此这里还不是很能体现反向传播的用法。我们会通过接下来的迭代来体现。

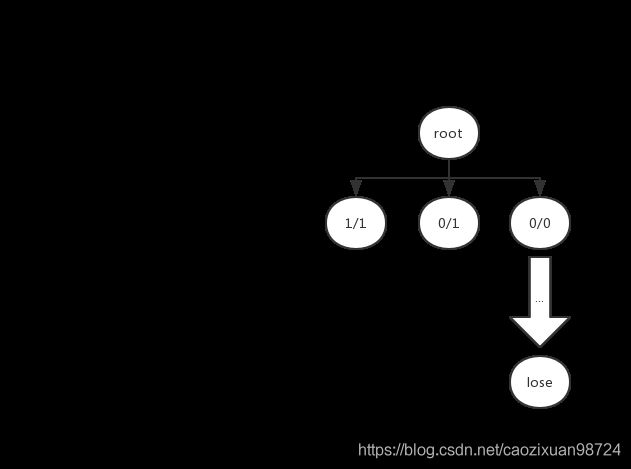
第二次迭代与第三次迭代：

这两次迭代是一样的，因为我们根据UCB公式，未被访问过的节点其值是正无穷，也就是说，是一定会被选择到的。我们假设这两次模拟的结果都是失败（最右侧节点的值忘记更新了）。

第四次迭代：

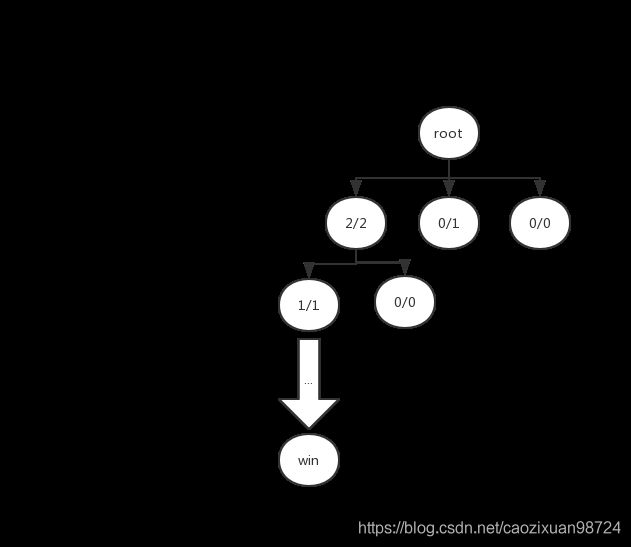
这一次迭代，我们假设是最左侧节点的UCB值最大，再此节点的基础上进行扩展。我们假设可以扩展出两个节点。注意要不断更新其父节点的值。

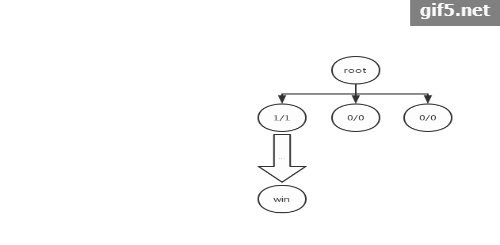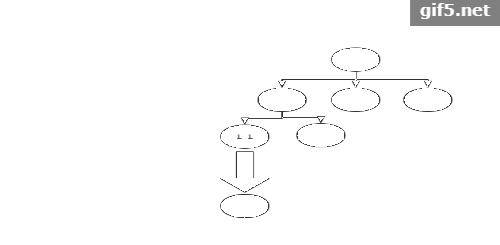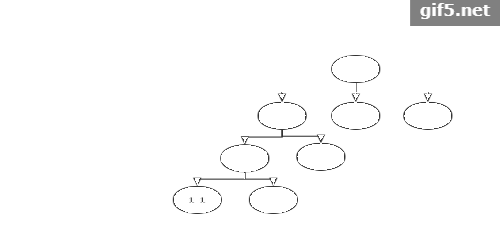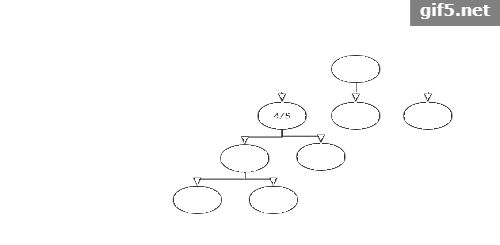
多次迭代：

后面的迭代过程大同小异，我做了一个粗糙的动图来展示整个过程，最需要注意的就是反向传播的问题。

4. 蒙特卡洛搜索树算法的实现

前几天尝试过自己实现一下这个算法，很可惜，出了一些bug，目前还没有调试出问题所在。所以只能用别人写好的现成的代码讲了。我参考的是github上的实现mcts，这个代码已经被封装成了package，可以简单的调用，我觉得它很好的一点是可以指定模拟的时间，而且其实现非常的简单，完全按照上述给的算法伪代码实现的。在讲解完这份代码后，我会用其实现一个基于蒙特卡洛搜算算法的智障五子棋AI(智障点明了这个AI根本无法使用)。

4.1 TreeNode树节点类

class treeNode():
    def __init__(self, state, parent):
        self.state = state
        self.isTerminal = state.isTerminal()
        self.isFullyExpanded = self.isTerminal
        self.parent = parent
        self.numVisits = 0
        self.totalReward = 0
        self.children = {}

这个类一共包括了7个属性。

state需要我们自己去定义这个类，后面例子中会讲到。

isTerminal是代表当前的状态是否是终结态，从这里我们也可以看到，isTerminal()是我们在state类中一定要实现的方法。

isFullyExpanded是指节点是否完全扩展，不理解这个意思的可以回头看第三节的算法描述和举例。

parent就是指当前节点的父节点。

numVisits代表节点被访问的次数。

totalReward是获取的奖励，如果我们定义1为胜利，0为失败，那么我们在上文中定义的3/4之类就可以表达为totalReward/numVisits。

children是当前节点的子节点的集合。

4.2 选择

def getBestChild(self, node, explorationValue):
        bestValue = float("-inf")
        bestNodes = []
        for child in node.children.values():
            nodeValue = child.totalReward / child.numVisits + explorationValue * math.sqrt(
                2 * math.log(node.numVisits) / child.numVisits) # UCB公式
            if nodeValue > bestValue:
                bestValue = nodeValue
                bestNodes = [child]
            elif nodeValue == bestValue:
                bestNodes.append(child)
        return random.choice(bestNodes)  # 如果有多个节点值相等，从中随机选择一个。

我们前文已经讲的非常清楚了，我们要计算所有节点的UCB值，从中选取最大的那个，以解决“探索和利用难题”。

4.3 扩展

def expand(self, node):
        actions = node.state.getPossibleActions()
        for action in actions:
            if action not in node.children:
                newNode = treeNode(node.state.takeAction(action), node)
                node.children[action] = newNode
                if len(actions) == len(node.children):
                    node.isFullyExpanded = True
                return newNode

        raise Exception("Should never reach here")

这个地方又出现了我们自己写的state要实现的几个方法，getPossibleActions,takeAction。

这里的逻辑也很简单，我们获取当前状态下所有可能的动作，把没有加入的动作导致的state全部加进来，就能够得到fullyexpanded的节点了。

4.4 模拟

def search(self, initialState):
        self.root = treeNode(initialState, None)

        if self.limitType == 'time':
            timeLimit = time.time() + self.timeLimit / 1000
            while time.time() < timeLimit:
                self.executeRound()
        else:
            for i in range(self.searchLimit):
                self.executeRound()

        bestChild = self.getBestChild(self.root, 0)
        return self.getAction(self.root, bestChild)

    def executeRound(self):
        node = self.selectNode(self.root)
        reward = self.rollout(node.state)
        self.backpropogate(node, reward)

    def selectNode(self, node):
        while not node.isTerminal:
            if node.isFullyExpanded:
                node = self.getBestChild(node, self.explorationConstant)
            else:
                return self.expand(node)
        return node

这一段代码糅合了很多东西，简单来说，就是选择了节点，不找到terminal绝不停止，找到了就返回reward，然后反向传播。

4.5 反向传播

这个最简单了，从当前节点开始，一直往上走就可以了。

def backpropogate(self, node, reward):
        while node is not None:
            node.numVisits += 1
            node.totalReward += reward
            node = node.parent

完整的代码见https://github.com/pbsinclair42/MCTS/blob/master/mcts.py

5. 基于蒙特卡洛搜索算法的五子棋示例

我们主体是要实现两个类，state类和action类。

class GoBangState():
    
    def __init__(self,board, currentPlayer=1, last_move = [0,0]):
        self.board = board   #五子棋棋盘
        self.currentPlayer = currentPlayer  # 执黑还是执白，1是黑，-1是白
        self.last_move = last_move # 上一手棋的位置

    def getPossibleActions(self):
        """
        最开始考虑用以下的代码，但是搜索空间实在是太大了
                possibleActions = []
                for i in range(len(self.board)):
                    for j in range(len(self.board[i])):
                        if self.board[i][j] == 0:
                            possibleActions.append(Action(player=self.currentPlayer, x=i, y=j))
                return possibleActions

        """
        # 此处改成在上一手棋周围进行搜索
        possibleActions = []
        search_size = 1
        while len(possibleActions)==0:
            for i in range(self.last_move[0]-search_size,self.last_move[0]+search_size+1):
                for j in range(self.last_move[1]-search_size,self.last_move[1]+search_size+1):
                    if i<0 or j<0 or i>=len(self.board) or j>=len(self.board[i]):
                        continue
                    if self.board[i][j] == 0:
                        possibleActions.append(Action(player=self.currentPlayer, x=i, y=j))
            search_size+=1
        return possibleActions



    def takeAction(self, action):
        newState = deepcopy(self)
        newState.board[action.x][action.y] = action.player
        newState.currentPlayer = self.currentPlayer * -1
        return newState

    def isTerminal(self):
        # judge函数引自https://www.jianshu.com/p/cd3805a56585
        flag = judge(self.board)
        if flag!=0:
            return True
        # 要注意无处落子的情况
        for i in range(len(self.board)):
            for j in range(len(self.board[i])):
                if self.board[i][j]==0:
                    return False
        return True

    def getReward(self):
        flag = judge(self.board)
        return flag

class Action():
    def __init__(self, player, x, y):
        self.player = player
        self.x = x
        self.y = y

    def __str__(self):
        return str((self.x, self.y))

    def __repr__(self):
        return str(self)

    def __eq__(self, other):
        return self.__class__ == other.__class__ and self.x == other.x and self.y == other.y and self.player == other.player

    def __hash__(self):
        return hash((self.x, self.y, self.player))

下面附上judge函数，来自https://www.jianshu.com/p/cd3805a56585：

def judge(board):
    for n in range(15):
        # 判断垂直方向胜利
        flag = 0
        # flag是一个标签，表示是否有连续以上五个相同颜色的棋子
        for b in board:
            if b[n] == 1:
                flag += 1
                if flag == 5:
                    return 1
            else:
                # else表示此时没有连续相同的棋子，标签flag重置为0
                flag = 0

        flag = 0
        for b in board:
            if b[n] == 2:
                flag += 1
                if flag == 5:
                    return -1
            else:
                flag = 0

        # 判断水平方向胜利
        flag = 0
        for b in board[n]:
            if b == 1:
                flag += 1
                if flag == 5:
                    return 1
            else:
                flag = 0

        flag = 0
        for b in board[n]:
            if b == 2:
                flag += 1
                if flag == 5:
                    return -1
            else:
                flag = 0

        # 判断正斜方向胜利

        for x in range(4, 25):
            flag = 0
            for i, b in enumerate(board):
                if 14 >= x - i >= 0 and b[x - i] == 1:
                    flag += 1
                    if flag == 5:
                        return 1
                else:
                    flag = 0

        for x in range(4, 25):
            flag = 0
            for i, b in enumerate(board):
                if 14 >= x - i >= 0 and b[x - i] == 2:
                    flag += 1
                    if flag == 5:
                        return -1
                else:
                    flag = 0

        # 判断反斜方向胜利
        for x in range(11, -11, -1):
            flag = 0
            for i, b in enumerate(board):
                if 0 <= x + i <= 14 and b[x + i] == 1:
                    flag += 1
                    if flag == 5:
                        return 1
                else:
                    flag = 0

        for x in range(11, -11, -1):
            flag = 0
            for i, b in enumerate(board):
                if 0 <= x + i <= 14 and b[x + i] == 2:
                    flag += 1
                    if flag == 5:
                        return -1
                else:
                    flag = 0
    return 0

获取输出的调用代码如下：

state = GoBangState(board._board,-1,[row,col])
m = mcts(timeLimit=30000,rolloutPolicy=weightPolicy)
action = m.search(initialState=state)

完整的代码就不放出来了，只是做一个示例，里面抄袭别人代码的内容太多了，哪天全部替换成自己写的代码了再放上去，哈哈哈！

6. 参考

Introduction to Monte Carlo Tree Seach

蒙特卡洛搜索算法的python实现

python实现的基于蒙特卡洛树搜索(MCTS)与UCT RAVE的五子棋游戏

蒙特卡洛搜索

python五子棋

文章中可能会出现不少错误，欢迎大家批评指正！