线性降维：PCA、LDA、MDS

1. KNN

为什么要在介绍降维之前学习KNN呢？因为以KNN为代表的一类算法，由于其为非参数化模型，无法通过一组固定的参数和固定的模型进行表征。此外，KNN还是惰性学习算法的典型例子。惰性是指它仅仅对训练数据集有记忆功能，而不会从训练集中通过学习得到一个判别函数。惰性学习算法一般思想简单，且没有训练过程。与之相对应的则是急切学习，需要以数据集为基础进行训练建模、总结规律，然后利用测试集对建立的模型进行测试。KNN为代表的一类算法，即没有参数、不需要训练过程，也无法使用例如在损失函数中加入正则项之类的方法对维度系数进行约束，所以易造成过拟合，进而导致传说中的维度风暴。

1.1 KNN思想及特性

KNN，即K-Nearest Neighbor，又称K近邻算法，是一个理论上非常成熟的算法，也是最简单的算法之一。

该算法的思路也确实简单：如果一个样本在特征空间中的K个最相似（即特征空间中按照某个度量计算的距离最近）的样本中大多数属于某一个类别，则该样本也属于这个类别。如上图中所示，对于绿色的点，观察与它距离最近的三个点，其中两个为红色三角形，则判定绿色的点也属于红色三角形所属的类。

KNN中的K表示选择的最近邻数量，不同的K值对分类结果影响很大，同样如上图所示，如果选择K=3，图中实线圈所示，可将绿色样本判定为红色三角形类；如果选择K=5，图中虚线圈所示，蓝色方块数量较多，可判定属于蓝色方块所属类。可见选择不同的K值，可以产生不同的分类结果。

这种基于记忆的学习算法最明显的优点在于可以快速的适应新的训练数据。缺点也显而易见，随着样本数量的增多，计算复杂度也随之增加，必须使用高效的数据结构（如KD Tree等）才能一定程度上提高计算速度。但随着训练样本数量的增多，不仅对存储空间占用明显，数据从硬盘调度时间也会极大影响计算速度。

此外，KNN还具有精度高，即使与SVM/DF/RF相比也好不逊色，且随着K值得增加，算法对异常值的容忍度也越来越高。KNN还有一个明显特点就是，只要给定训练集、距离度量、K值以及分类决策，其分类结果是唯一的，故不适合作为集成学习中的弱学习器。

1.2 KNN实现流程

KNN算法描述如下：
输入：训练数据集$T=\{(x_i,y_i),i=1,2,3,...,N\}$，其中$x_i\in R^n$为实例的特征向量，$y_i\in \{c_i,i=1,2,3,...,K\}$\为样本所属类别。
输出：实例x所属于的类别y。
根据给定的距离度量，在训练集T中找出与x最近的K个点，涵盖这K个点的x的领域记为$N_k(x)$。
根据分类决策（如多数表决等）决定x所属的类别y。
$$\begin{gathered} y=arg\underset{c_i}{\max }\sum _{x\in N_i(x)}I(y_i=c_j) \\ i=1,2,3,...,N;j=1,2,3,...,K \end{gathered}$$

上式中，$I$为指示函数，即当$y_i=c_j$时$I=1$，否者$I=0$。
从以上流程中可以看出，当训练集、距离度量、K值和分类决策确定后，对于任何一个输入实例。其所属的类是唯一确定的。使用KNN对数据进行处理前，还需要对数据进行标准化操作，归一化或标准化（标准正态分布）均可。在sklearn中已经集成了KNN模块，可以非常方便的调用：

from sklearn.neighbors import KNeighborsClassifier
knn = KNeighborsClassifier(    	
	n_neighbors=5,    
	p=2,    
	metric='minkowski'
)
knn.fit(X_train_std, y_train)

代码中，n_neighbors表示近邻数，即为K值，metric表示采用的度量，此为闵可夫斯基距离，P为闵可夫斯基距离的权值。

1.3 KNN与度量

距离度量的选择对于KNN分类结果的影响不言而喻，常用的度量包括以下几种。

闵可夫斯基距离

闵可夫斯基距离（Minkovski Distance），又称闵式距离，不是一种距离，是一类距离的定义。对于两个n维变量$a(x_{11},x_{12},...,x_{1n})$和$b(x_{21},x_{22},...,x_{2n})$之间的闵式距离定义为：
$$d_{12}={\left(\underset{k=1}{\sum ^n}|x_{1k}-x_{2k}{|}^p\right)}^{\frac{1}{p}}$$
其中p是一个变参数：
当$p=1$时，闵式距离为曼哈顿距离；
当$p=2$时，闵式距离为欧氏距离；
当$p=+\infty$，闵式距离就变为切比雪夫距离，即对应参数相减的绝对值最大值：
$$L_p=\underset{l}{max|x_i^{(l)}-x_j^{(l)}|}$$

马氏距离

根据经验我们知道，如果数据没有进行标准化操作，不同特征的度量标准没有统一，直接使用欧式距离进行度量会导致判断出错。马氏距离是一种有效的计算两个位置样本相似度的方法。与欧式距离不同的是其考虑到各种特性之间的联系，并且这种联系与尺度无关，即独立于测量尺度。

先回顾一些协方差的定义，$Cov(X,Y)=E[(X-{\mu }_x)(Y-{\mu }_y)]$协方差用于衡量两个变量的总体误差，方差是协方差的一种特殊情况。简单的描述就是：两个变量在变化过程中是否为同向变化？同向或反向变化的程度如何？丛数值来看，协方差数值越大，说明两个变量同向变化的程度就越大，反之亦然。协方差代表了两个变量之间是否同时偏离均值，以及偏离的方向是同向还是反向。

马氏距离的定义为，用来衡量一个样本P和数据分布D的集合的距离。假设样本点为：$x=(x_1,x_2,x_3,...,x_N{)}^T$，数据集的分布的均值为：$\mu =({\mu }_1,{\mu }_2,{\mu }_3,...,{\mu }_N{)}^T$，协方差矩阵为S，此时协方差矩阵S中的元素为数据集中各个特征向量之间的协方差。则这个样本P与数据集合的马氏距离为：
$$D_M(x)=\sqrt{(x-\mu {)}^T{S}^{-1}(x-\mu )}$$
马氏距离也可以用来衡量两个来自同一分布的样本x和y之间的相似性：
$$d(x,y)=\sqrt{(x-y{)}^T{S}^{-1}(x-y)}$$
当样本集合的协方差矩阵是单位矩阵时，即样本在各个维度上的方差都是1时，马氏距离等同于欧式距离。

1.4 KNN存在的问题和维度灾难

使用KNN算法存在一些问题，一是实例间的距离是根据实例的所有属性计算的，所以近邻间的距离会被大量不相关的属性所支配；二是KNN算法必须保存全部数据集并计算相互之间的距离，如果数据集较大，实际使用中会消耗大量的存储空间和计算时长；三是训练数据集中要求的观测值数量会随着维数K增长以指数方式增长。

此外由于KNN的特性，其非常容易过拟合。维度灾难是指，对于一个样本数量稳定的训练数据集，随着特征数量的增加，样本中具体值的特征数量变得极其稀疏（大多数特征的取值为0）。从而导致在这样的高维空间中，即使是最近邻，距离也非常远，难以给出一个合适的类别判定。而且在高维空间训练的线性分类器，相当于低维空间中的复杂非线性分类器，从这个角度来看KNN非常容易过拟合。在参数化模型中，如逻辑斯谛回归和线性回归中可以通过正则化使其避免过拟合，但对于非参数化的KNN、决策树等算法则无法使用正则化方法。

综合上述原因，如果随着维度的增加样本数量没有随之增加，就必须使用降维技术，如主成分分析、变量选择等技术减少计算复杂度和所需时间，避免过拟合，降低估计误差。

2.线性降维

我们可以采用特征抽取（即降维）来减少数据集中特征的数量。降维可以认为是在尽可能保持相关信息的基础上，对数据进行压缩的一种方法。降维可以提高计算效率，同样也可帮助我们避免“维度灾难”尤其是在模型不适用于正则化处理时。

2.1 主成分分析（PCA）

主成分分析（Principal Component Analysis，简称PCA）是广泛应用于不同领域的无监督线性数据转换技术。降维的一个基本要求是能够保持数据的原始特征，即本质信息。PCA虽然从原理上分析会导致一部分信息的损失，但会基于特征之间的关系实现压缩或合并冗余特征，保留其中有价值的信息。

原理简述

最大方差理论。在信号处理中认为信号具有较大方差，噪声具有较小方差，而信噪比（即信号和噪声方差的比）越大越好。空间中可以定义无数个基（坐标系）。以二维空间为例，可以在空间中找到一个特定的坐标系，所有样本在其中一个坐标上的方差最大，甚至都不需要第二个坐标值就可以对样本进行区分，推广到多为空间也是如此。我们认为，最好的d维特征是将n维样本转换为d维后（其中d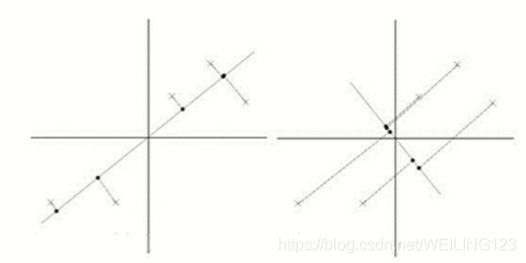
如上图所示，将5个中心化处理后的数据投影到某两个用直线表示的一维超平面上，明显可以看出，左边的投影效果更好，样本之间的方差最大，该情况下即投影后的绝对值之和最大，原有样本特征依然保持了原有的差异性。PCA降维就是要使用线性代数的方法找到这个使得样本在其上变化最大的坐标系，表示如下：
$$\begin{gathered} x=\left[x_1,x_2,...,x_d\right],x\in {\mathbb{R}}^d \\ \downarrow xW,W\in {\mathbb{R}}^{d\times k} \\ z=\left[z_1,z_{tiny2},...,z_k\right],z\in {\mathbb{R}}^k \end{gathered}$$
完成上述从d维到k维的转换后，第一主成分的方差值为最大，后续主成分也具备较大的方差。需要注意的是，由于主成分方向对于数据范围较为敏感，如果特征的值使用不同的度量标准，需要首先对数据进行标准化处理。

实现流程

1）对原始d维数据做标准化处理

2）构造样本的协方差矩阵
协方差表示了不同不同特征之间的变化趋势。若数据特征数量为d，则协方差矩阵为d*d维且沿对角线对称，其中每个数值表示对应特征之间的协方差，例如对于特征$x_j$和$x_k$之间的协方差可以表示为：
$${\sigma }_{jk}=\frac{1}{n}\underset{i=1}{\sum ^n}\left(x_j^{(i)}-{\mu }_j\right)\left(x_k^{(i)}-{\mu }_k\right)$$
其中j、k为维度序号，i为样本序号，$\mu$为某个特征在样本中的均值。

3）计算协方差矩阵的特征值和相应的特征向量
协方差矩阵的特征向量代表主成分（方差最大方向），而对应的特征值大小决定了特征向量的重要性。若协方差矩阵表示为$\sum$，特征值和特征向量关系表示为：$\sum W=\lambda W$。

4）选择与前k个最大特征值对应的特征向量
其中K为新特征空间的维度，通过前K个特征向量构建映射矩阵W。k值需要用户实现确定，或通过取不同的K’值所对应的不同低维空间映射，对数据降维后利用分类器进行交叉验证，最终确定较好的k值。此外还可以引入特征值的方差贡献率，通过累积方差贡献率并设置阈值来确定K值。特征值${\lambda }_i$的方差贡献率为：
$$e_i=\frac{{\lambda }_i}{\stackrel{d}{\sum _{j=1}}{\lambda }_j}$$
其中i表示特征值从大到小排列的序号。若设置阈值t=0.9，则选择使得下式成立的最小k值:
$$\frac{\stackrel{k}{\sum _{i=1}}{e}_i}{\stackrel{d}{\sum _{i=1}}{e}_i}\ge t$$

6）通过映射矩阵W将d维的输入数据集X转换到新的K维特征子空间
通过pca降维处理后的低维空间肯定和原始的高维空间有所不同，因为对应于最小的d-k个特征值的特征向量被舍弃，样本对应维度的信息也随之舍弃，使得样本的采样密度增大，避免了样本稀疏的问题。同时，当数据收到噪声影响时，最小特征值所对应特征向量往往与噪声有关，将其舍弃在一定程度上起到去噪的效果。

代码示例1：从原理实现

同样，作为一种成熟稳定的算法，在sklearn中已经集成了PCA模块，直接调用即可。未说明算法原理，现以著名的葡萄酒数据集为例，说明如何实现PCA算法。
1）读取数据
从本地读取wine.data文件，将数据保存在DataFrame对象中并设置列名，最后通过head()方法对数据进行初步探索。

import pandas as pd 

data_dir = 'e:/data/'
data_path = data_dir + 'wine.data'
df_wine = pd.read_csv(data_path, header=None)
df_wine.columns = ['Class label', 'Alcohol', 'Malic acid', 'Ash',    'Alcalinity of ash', 'Magnesium', 'Total phenols',    'Flavanoids', 'Nonflavanoid phenols', 'Proanthocyanins',    'Color intensity', 'Hue', 'OD280/OD315 of diluted wines','Proline']
print(df_wine.head())

显示结果为：

   Class label  Alcohol  ...  OD280/OD315 of diluted wines  Proline
0            1    14.23  ...                          3.92     1065
1            1    13.20  ...                          3.40     1050
2            1    13.16  ...                          3.17     1185
3            1    14.37  ...                          3.45     1480
4            1    13.24  ...                          2.93      735

2）将数据分割为训练集和测试集，并对数据进行标准化操作

# 数据分割
from sklearn.model_selection import train_test_split
# dataframe->数组array
X, y = df_wine.iloc[:,1:].values,df_wine.iloc[:,0].values
X_train, X_test, y_train, y_test =train_test_split(
X, y, test_size=0.3,stratify=y,random_state=0)
# 标准化，将所有特征数据都转换为标准正态分布的范围内
from sklearn.preprocessing import StandardScaler
sc = StandardScaler()
X_train_std = sc.fit_transform(X_train)
# 不能再次fit_transform()，使用训练集中的参数
X_test_std = sc.transform(X_test)

3）计算训练集的协方差矩阵
通过numpy模块中的cov可以直接计算数组的协方差矩阵。

import numpy as np 
# cov方法输入数组的行（row）表示特征，列（column）为样本，所以需要对原有的数组求转置
cov_mat = np.cov(X_test_std.T)
print(cov_mat)     #协方差矩阵为对称方阵

输出结果：

[ 0.89469011  0.13667696  0.2877508  -0.23136694  0.3083033   0.27920024
   0.24674112 -0.35485714  0.16823986  0.50330242 -0.37681333  0.28236162    
   0.55499891]
 [ 0.13667696  0.70749789  0.33455847  0.30176631  0.0917766  -0.31125658    
  -0.33660816  0.17318595 -0.1915928   0.37264897 -0.57245046 -0.26539649    
  -0.03668203]
 [ 0.2877508   0.33455847  1.12162652  0.39489721  0.34468053  0.00489061    
   0.00667412  0.25709411  0.00348201  0.38515574 -0.27183031 -0.03948387    
   0.20808148]
 [-0.23136694  0.30176631  0.39489721  0.9596675  -0.07895091 -0.47882999    
  -0.44984131  0.4766308  -0.13040005  0.25810396 -0.41589041 -0.56858296    
  -0.37002113]
 [ 0.3083033   0.0917766   0.34468053 -0.07895091  1.09196325  0.16221445    
   0.17525977 -0.27137892  0.35365767  0.19306104 -0.12070222  0.07951528    
   0.33021925]
 [ 0.27920024 -0.31125658  0.00489061 -0.47882999  0.16221445  1.1024704     
   0.84492294 -0.54601485  0.54096273 -0.05703593  0.35596724  0.76330517    
   0.39991782]
 [ 0.24674112 -0.33660816  0.00667412 -0.44984131  0.17525977  0.84492294    
   0.85747051 -0.54880323  0.54527596 -0.18939484  0.44287668  0.79546035    
   0.33236332]
 [-0.35485714  0.17318595  0.25709411  0.4766308  -0.27137892 -0.54601485    
  -0.54880323  1.16251249 -0.32244964  0.00345336 -0.07668603 -0.43564806    
  -0.25183415]
 [ 0.16823986 -0.1915928   0.00348201 -0.13040005  0.35365767  0.54096273    
   0.54527596 -0.32244964  0.74674097 -0.08139845  0.25763795  0.54079595    
   0.25456883]
 [ 0.50330242  0.37264897  0.38515574  0.25810396  0.19306104 -0.05703593    
  -0.18939484  0.00345336 -0.08139845  0.8813149  -0.70697515 -0.35940024    
   0.25476159]
 [-0.37681333 -0.57245046 -0.27183031 -0.41589041 -0.12070222  0.35596724    
   0.44287668 -0.07668603  0.25763795 -0.70697515  1.23820758  0.51095039    
  -0.02747201]
 [ 0.28236162 -0.26539649 -0.03948387 -0.56858296  0.07951528  0.76330517    
   0.79546035 -0.43564806  0.54079595 -0.35940024  0.51095039  1.16534479    
   0.41466515]
 [ 0.55499891 -0.03668203  0.20808148 -0.37002113  0.33021925  0.39991782    
   0.33236332 -0.25183415  0.25456883  0.25476159 -0.02747201  0.41466515    
   0.78366947]]

输出结果为一个13*13的对称矩阵，而对称矩阵可以进行特征值分解，并得到正交的特征向量。

4）求解特征值和特征向量并绘制累加图
使用numpy中eig方法对数组进行特征值分解，并对特征值进行排序输出。

# 特征值分解
eigen_vals, eigen_vecs = np.linalg.eig(cov_mat)
tot = sum(eigen_vals)
# 计算特征值的方差贡献率
# sorted()方法是升序，reverse=True表示降序
var_exp = [i/tot for i in sorted(eigen_vals, reverse=True)]
# 特征值得累计和，最终结果为1
cum_var_exp = np.cumsum(var_exp)
print(cum_var_exp)

输出结果为：

[0.36251814 0.5907884  0.69407243 0.767845   0.82961586 0.87144802
 0.91106622 0.93879609 0.95951489 0.97576861 0.9858895  0.99462381
 1.        ]

以此为基础可以画出柱状图和累加图

import matplotlib.pyplot as plt  
plt.bar(
    range(1,14),var_exp,    
    alpha=0.5,align='center',    
    label='individual explained variance'
)
plt.step(
    range(1,14),cum_var_exp,
    where='mid',
    label='cumulative explained variance'
)
plt.ylabel('Explained variance ratio')
plt.xlabel('Principal component index')
plt.legend(loc='best')
plt.tight_layout()plt.show()

显示结果为：

从图中可以看出，前两个特征的方差贡献率累加已超过0.6。

5）转换矩阵、降维、可视化

# 获取特征值和对应的特征向量,list中是一个元组tuple
eigen_pairs = [    
	(eigen_vals[i], eigen_vecs[:,i])    
	for i in range(len(eigen_vals)) 
]
# 按照tuple中的特征值进行排序
eigen_pairs.sort(key=lambda k: k[0],reverse=True)
# 取最大两个特征值对应的特征向量，拼接为转换矩阵 
# 合并二维矩阵，原有的特征向量为一维数组，需要利用np.newaxis添加一个维度以便拼接 
w = np.hstack((eigen_pairs[0][1][:,np.newaxis],
		eigen_pairs[1][1][:,np.newaxis]))
print(w)

得到的转换矩阵为：

[[-0.12999701  0.43638363]
 [ 0.2045815   0.24534465]
 [ 0.08570227  0.37095787]
 [ 0.31941304  0.06403434]
 [-0.10668011  0.33500347]
 [-0.41039418  0.09979891]
 [-0.39670979  0.04728298]
 [ 0.31182429 -0.1322099 ]
 [-0.27102652  0.09017136]
 [ 0.141004    0.43780094]
 [-0.27880867 -0.42008522]
 [-0.42829415  0.00338996]
 [-0.2072508   0.29913089]]

通过将样本数据点乘转换矩阵即可实现降维：

X_train_pca = X_train_std.dot(w)
print(X_train_pca.shape)

输出为：

(124, 2)

此时数据从原有的13维降为2维，可以在二维平面中以散点图的形式显示出来：

colors = ['r','b','g']
markers = ['s','x','o']
for l,c,m in zip(np.unique(y_train), colors, markers):    
	plt.scatter(        
		X_train_pca[y_train == l,0],        
		X_train_pca[y_train == l,1],        
		c=c, label=l, marker=m    
	)
plt.xlabel('PC 1')
plt.ylabel('PC 2')
plt.legend(loc='lower left')
plt.tight_layout()
plt.show()

显示为：

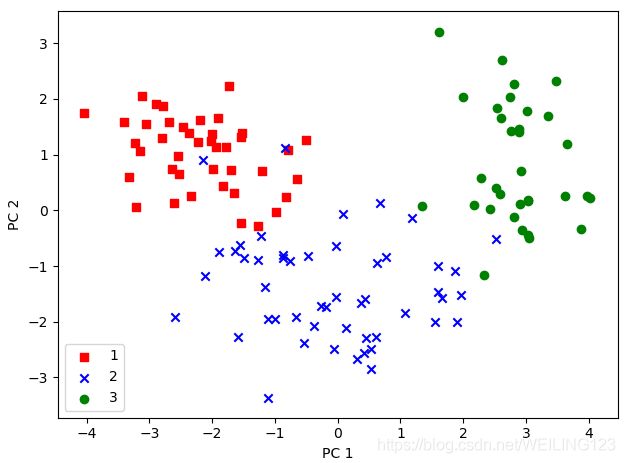
从图中可以看出，数据分类明显，且在PC1和PC2方向上方差较大。

代码示例2：sklearn实现

直接调用sklearn.decomposition中的PCA模块，可替代上述的3）、4）、5）过程：

from sklearn.decomposition import PCA
# 降维后只选取其中的两个特征
pca = PCA(n_components=2)
X_train_pca = pca.fit_transform(X_train_std)
print(X_train_pca.shape)

输出结果为：

(124, 2)

2.2 线性判别分析（LDA）

LDA和PCA都是可以用与降低数据集维度的线性转换技巧。两者的基本概念非常相似，PCA试图在数据集中找到方差最大的正交的主成分分量的轴，LDA的目标则是发现可以最优化分类的特征子空间。但是，不同于PCA算法，LDA是有监督算法，是以最适合已有的分类作为导向。

原理简述

LDA的基本思想是将样本从高维空间投影到最佳鉴别矢量空间，以达到抽取分类信息和压缩空间维数的效果。投影后保证样本在新的子空间中类内方差最小二类间方差最大，即该空间具有最佳可分离性。

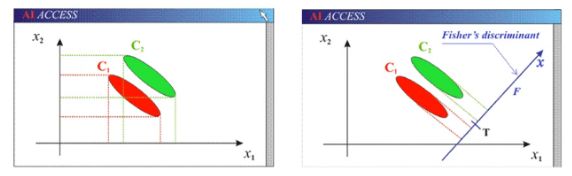
如上图中左图所示，图中数据包括一个绿色类别和红色类别。要求将数据从二维降到一维，如直接投影到X1轴或X2轴，不同类别之间都会有重复，导致分类结果下降。LDA算法可以得到一条直线，如右图所示，红色类别和绿色类别在映射后距离最大，并且每个类别内部点的离散程度最小。

不同于PCA中从协方差矩阵角度寻找最佳投影，LDA采用散度矩阵。散度矩阵和协方差矩阵基本一致，只是散度矩阵在累加之后没有除以总量。通过均值向量，可以得到类内散布矩阵$S_W$：
$$\begin{gathered} S_w=\stackrel{c}{\sum _{i=1}}{S}_i \\ {S}_i=\stackrel{c}{\sum _{x\in D_i}}(x-m_i)(x-m_i{)}^T \\ {m}_i=\frac{1}{n_i}\sum _{x\in D_i}x \end{gathered}$$
其中$m_i$为各个类别的均值向量。如果对散布矩阵进行归一化，就可得到协方差矩阵：
$$\sum _i=\frac{1}{N}{S}_W=\frac{1}{N}\sum _{x\in D_i}(x-m_i)(x-m_i{)}^T$$
同理，类间散布矩阵为：
$$S_B=\stackrel{c}{\sum _{i=1}}{N}_i(m_i-m)(m_i-m{)}^T$$
其中m为全局均值，由所有样本计算得到。

假设二分类情况，用来区分二分类的直线为$y=w^{T}x$，类别i的投影后中心点为：$m_i=w^T{m}_i$。同样，投影后的类内散度矩阵为：
$$S_i=\sum _{y\in D_i}(y-m_i)(y-m_i{)}^T$$
为了达到类内方差最小，类间方差最大的优化目的，构建如下目标优化函数：
$$J(w)=\frac{|m_1-m_2{|}^2}{{s_1}^2+{s_2}^2}$$
上式中，分母表示每一个类别内的方差之和，方差越大表示类别内的点越分散，分子为各个类别中心点的距离的平方，我们的目的就是要找到使得优化函数分子最小（类间距离最大），分母最小（类内散度最小）的最优化w。优化通过化简得到：
$$J(w)=\frac{w^T{S}_{B}w}{w^T{S}_{w}w}$$
使用拉格朗日算子方法将问题转换为求解下式（fisher线性判别式）中w的特征向量：
$$S_W^{-1}{S}_{B}w=\lambda w$$
最后，再使用类似PCA中的方式选取特征向量构造转换矩阵W。

实现流程

1）对d维数据进行标准化处理；
2）对于每一类别，计算d维的均值向量；
3）构造类间的散布矩阵$S_B$以及类间散布矩阵$S_W$
4）计算矩阵$S_W^{-1}{S}_B$的特征向值以及对应的特征向量；
5）选取前k个特征值所对应的特征向量，构造一个d*k维的转换矩阵W，其中的特征向量以列的形式排列；
6）使用转换矩阵W经样本映射到新的特征空间中。

代码示例

同样以红酒数据为例：
1）从本地读取数据，数据分割以及标准化

import pandas as pd
import matplotlib.pyplot as plt 
import numpy as np 
data_dir = 'e:/data/'
data_path = data_dir + 'wine.data'
df_wine = pd.read_csv(data_path, header=None)
df_wine.columns = [    'Class label', 'Alcohol', 'Malic acid', 'Ash',    'Alcalinity of ash', 'Magnesium', 'Total phenols',    'Flavanoids', 'Nonflavanoid phenols', 'Proanthocyanins',    'Color intensity', 'Hue', 'OD280/OD315 of diluted wines',    'Proline']
# 数据分割
from sklearn.model_selection import train_test_split
X, y = df_wine.iloc[:,1:].values, df_wine.iloc[:,0].values
X_train, X_test, y_train, y_test = train_test_split(    
	X, y, test_size=0.3, stratify=y, random_state=0
)
# 标准化，将所有特征数据都转换为标准正态分布的范围内
from sklearn.preprocessing import StandardScaler
sc = StandardScaler()
X_train_std = sc.fit_transform(X_train)
X_test_std = sc.transform(X_test)

2）求类内散布矩阵$S_W$

# 类别数量
label_num = np.unique(y_train).shape[0]
# 设置小数点后的精度，保留4位
np.set_printoptions(precision=4)
# 获取均值向量
mean_vecs = []
# 处理每一个类别的样本数据
for label in range(1,label_num+1):    
	mean_vecs.append(        
		np.mean(            
			X_train_std[y_train == label],            
			axis=0        
		)    
	)
# 参数个数
d = 13
# 初始化类内散度矩阵，大小肯定是13*13
S_W = np.zeros((d,d))	

# class_scatter是单个类别所有样本的散度矩阵
# 所有类别的散度矩阵求和的结果是类内散布矩阵
for label, mv in zip(range(1,label_num+1), mean_vecs):    
	class_scatter = np.zeros((d,d))    
	for row in X_train_std[y_train == label]:
		row, mv = row.reshape(d, 1), mv.reshape(d, 1)
		class_scatter += (row - mv).dot((row - mv).T)	
	# 每一类的类内散布矩阵	
	S_W += class_scatter     

3）计算类间散布矩阵

# 所有样本的均值
mean_overall = np.mean(X_train_std, axis=0)
# 初始化
d = 13
S_B = np.zeros((d,d))

for i, mean_vecs in enumerate(mean_vecs):    
	# n为每一类样本的数量 
	n = X_train[y_train == i+1, :].shape[0]    
	# 转换为列向量  
	mean_vecs = mean_vecs.reshape(d,1)
	mean_overall = mean_overall.reshape(d,1)      
	S_B += n * (mean_vecs - mean_overall).dot((mean_vecs - mean_overall).T)

4）求特征值和特征向量，并按照特征值排序，画累计图

 # 求特征值和特征向量
eigen_vals, eigen_vecs = np.linalg.eig(        	
	np.linalg.inv(S_W).dot(S_B)     
)
# 特征值和特征向量配对
eigen_pairs = [    
	(np.abs(eigen_vals[i]), eigen_vecs[:,i])    
	for i in range(len(eigen_vals))
]
# 按照特征值进行排序
eigen_pairs = sorted(    
	eigen_pairs, key = lambda k: k[0], everse=True
)

# 画累计图
tot = sum(eigen_vals.real)
discr = [    
	(i/tot)    
	for i in sorted(eigen_vals.real, reverse = True)
]
#累加计算
cum_discr = np.cumsum(discr)
plt.bar(    
	range(1,14), discr, alpha=0.5,align='center',        
	label='individual "discriminability"'
)
plt.step(    
	range(1,14), cum_discr, where='mid',
	label='cumulative "discriminability"'
)
plt.ylabel('"discriminability" ratio')   
plt.xlabel('Linear Discriminants')
plt.show()

累计图显示如下：

如图中所示，头部两个特征值包含了绝大部分信息，基本接近100%。

5）构建转换矩阵，实现数据的二维可视化

# 构建转换矩阵,最高的两个特征值对应的特征向量
w = np.hstack(    
	(        
		eigen_pairs[0][1][:, np.newaxis].real,        
		eigen_pairs[1][1][:, np.newaxis].real    
	)
)
# 降维转换
X_train_lda = X_train_std.dot(w)

# 数据在二维空间中显示
colors = ['r','b','g']
markers = ['s','x','o']
for l,c,m in zip(np.unique(y_train), colors, markers):    
	plt.scatter(        
		X_train_lda[y_train == l, 0],
		X_train_lda[y_train == l, 1] * (-1),        
		c=c, label=l, marker=m    
	)
plt.xlabel('LD 1')
plt.ylabel('LD 2')
plt.legend(loc = 'lower right')
plt.tight_layout()
plt.show()

显示结果如下：

从图中可以看到，不同类别数据分割明显，若使用线性分类器也能取得不错的分类效果。

2.3 多维缩放（MDS）

多维缩放也是一种经典的降维方法，其基本原则就是所有数据点对在低维空间中的距离和在高维空间中尽量保持一致，但距离度量的方法可能会不一致。

原理简述

假设有m个样本，其在原始空间中的距离矩阵为$D\in R^{m\times m}$，其中第i行j列元素$dis{t}_{ij}$为样本$x_i$到$x_j$的距离。

令样本在降维后的$d^{\prime }$维空间中的表示为$Z\in R^{d^{\prime }\times m},d^{\prime }\le d$，B为降维后样本的内积矩阵，$B=Z^{T}Z\in R^{m\times m}$，其中$b_{ij}=z_i^T{z}_j$。根据MDS算法原理，任意两个样本在$d^{\prime }$维空间中的欧式距离等于原始空间中的距离，即$||z_i-z_j||=dis{t}_{ij}$ ，平方展开后得到：
$$\begin{gathered} dis{t}_{ij}^2=||z_i-z_j|{|}^2 \\ =||z_i|{|}^2+||z_j|{|}^2-2z_i^T{z}_j \\ =b_{ii}+b_{jj}-2b_{ij} \end{gathered}$$
为了便于讨论，假设降维后的样本Z已被中心化，即${\sum }_{i=1}^m{z}_i=0$，显然矩阵B的行与列之和均为0，即${\sum }_{i=1}^m{b}_{ij}={\sum }_{j=1}^m{b}_{ij}=0$。又有：
$$\begin{gathered} \sum _{i=1}^{m}dis{t}_{ij}^2=\sum _{i=1}^m\left(||z_i|{|}^2+||z_j|{|}^2-2z_i^T{z}_j\right) \\ =\sum _{i=1}^m\left(b_{ii}+b_{jj}-2b_{b_{i}j}\right)=tr(B)+m{b}_{jj} \end{gathered}$$
同理：
$$\begin{gathered} \sum _{j=1}^{m}dis{t}_{ij}^2=tr(B)+m{b}_{ii} \\ \sum _{i=1}^m\sum _{j=1}^{m}dis{t}_{ij}^2=2mtr(B) \end{gathered}$$
其中$tr()$表示矩阵的迹，$tr(B)={\sum }_{i=1}^m||z_i|{|}^2$。通过观察以上几式得到降维后内积矩阵B和原始数据集距离矩阵D之间的关系：
$$b_{ij}=-\frac{1}{2}\left(dis{t}_{ij}^2-\frac{1}{m}\sum _{j=1}^{m}dis{t}_{ij}^2-\frac{1}{m}\sum _{i=1}^{m}dis{t}_{ij}^2+\frac{1}{m^2}\sum _{i=1}^m\sum _{j=1}^{m}dis{t}_{ij}^2\right)$$
得到内积矩阵B后，再对矩阵B做特征值分解，得到：
$$B=V\Lambda V^T$$
其中$\Lambda =diag({\lambda }_1,{\lambda }_2,...,{\lambda }_d)$为特征值构成的对角矩阵，其中$\lambda$按照只大小顺序排列。$V$为特征向量矩阵。假定有$d^{\ast }$个非零特征值，其构成的对角矩阵为${\Lambda }_{\ast }=diag({\lambda }_1,{\lambda }_2,...,{\lambda }_{d_{\ast }})$，相应的特征向量矩阵为$V_{\ast }$，则
$$B=V_{\ast }{\Lambda }_{\ast }{V}_{\ast }^T$$
结合$B=Z^{T}Z$得：
$$\begin{gathered} Z^{T}Z=V_{\ast }{\Lambda }_{\ast }{V}_{\ast }^T \\ Z={\Lambda }_{\ast }^{1/2}{V}_{\ast }^T\in R^{d^{\ast }\times m} \end{gathered}$$
实际应用中，仅需要降维后的距离和原始空间尽可能接近，不必严格相等，因此可将特征值中非常小的值舍弃，选取$d^{\prime }\ll d$个特征值构成的对角矩阵$\Lambda$以及对应的特征向量矩阵$V$，得到最终的矩阵Z为：
$$Z={\Lambda }^{1/2}{V}^T\in R^{d^{\prime }\times m}$$

步骤流程

1）对原始数据进行归一化预处理；
2）计算两两样本之间的欧式距离，获得原始数据的距离矩阵D；
3）利用上述公式计算降维后样本矩阵的内积矩阵B；
4）对矩阵的内积矩阵B做特征值分解，获得降维后矩阵Z。
如要使用MDS算法，可以直接从sklearn.manifold模块中调用MDS方法。

3. 小结

PCA、LDA以及MDS都是通过线性转换进行降维的算法，不同之处在于PCA是无监督的算法，其将数据映射到新的空间中，并且新的空间中某些维度的可分性最强；LDA是有监督的算法，在有标签的基础上寻找使得类内方差最小，类间方差最大的投影；而MDS则是以降维后样本间距离不变为基础，通过原始数据的距离矩阵逐步获得降维后样本矩阵。对于线性可分的数据，他们都能取得不错的降维效果，但如果数据无法表示为特征的线性组合，例如Helix曲线等，则很难使用线性降维方法。