SGU 147.Black-white king
时间限制:0.25s
空间限制:4M
题意:
在一个N*N(N <= 106)的棋盘上,有三个棋子:黑王、白王、黑白王,它们的行走方式一致,每秒向8个方向中的任意一个行走一步.
现在黑王和白王想要相遇(即占据相邻的格子),而黑白王需要阻止它们相遇,即抓住其中一个王(走到其中一个王所在的格子),
黑王和白王行走时总是走最短路径,而黑白王走的路径无法被缩短(即能够走斜向的时候,不会走Z字形),由于黑白王是隐身的,
所以黑王和白王无法看见黑白王的走向,但是他们知道有它存在,当黑王和白王走到黑白王所在的格子时不会有任何事情发生。
问黑白王是否有可能抓住其中一个王,如果有可能,输出最少步数;如果不可能,输出黑王和白王相遇总共的行走步数。行走顺序为白王、黑王、黑白王。
题解:
如果黑王和白王的y方向差值小于x方向差值,那么将三个棋子的x和y值分别交换。保证黑王和白王的y方向差值大于等于x方向差值,由于黑王和白王总是走他们能够相遇的最短路径,所以每次移动一定要保证在y方向朝对方移动一格,所以两个王的行走区域为朝着对方方向的一个“喇叭”形区域。
如图2所示,两个王的y方向坐标差值为T,黑王坐标(Bx, By),白王坐标(Wx, Wy),那么走i步后的黑王的y方向坐标为定值By + i * bDir,其中bDir为黑王到白王的方向;x方向的可行区间为[Bx – i, Bx + i]和[Wx – (T-i), Wx + (T-i)]的区间交集,即图中两个“喇叭”形区域的交集就是黑王和白王的可行区域,最多T-1步后两人相遇。
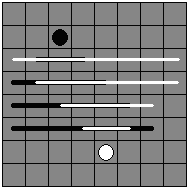
图4
黑白王的运动区域更加简单,如图3所示,灰色的方形外框表示经过3步后黑白王有可能在的位置,即一个长度为2i + 1的空心正方形区域。
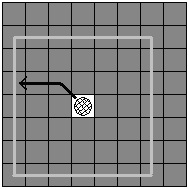
图5
于是,可以枚举步数,判断黑王和黑白王、白王和黑白王的第i步的区间区域是否有交集,如果一旦出现某个王在第i步的时候和黑白王的正方形区域有交集,则表明黑白王有可能在第i步抓住其中一个王,否则当2i >= T-1的时候还没有交集,表明黑王和白王已经相遇,总步数为T-1。总复杂度O(N)。
代码:
#include<stdio.h>
#include<algorithm>
using namespace std;
int n, d, st, ans;
struct Point
{
int x, y;
Point() {}
Point (int x, int y) : x (x), y (y) {}
void scan() { scanf ("%d%d", &x, &y); }
void print() { printf ("%d %d\n", x, y); }
};
Point b, w, bw, bl, br, wl, wr;
char res[2][5] = {"NO", "YES"};
int dis (Point a, Point b)
{
return max (abs (a.x - b.x), abs (a.y - b.y) );
}
int fail (Point k)
{
int d0 = dis (bw, Point (k.x, k.y) );
if (d0 > st) return 1;
else if (d0 < st) return -1;
return 0;
}
int main()
{
#ifndef ONLINE_JUDGE
freopen ("data.in", "r", stdin);
#endif
scanf ("%d", &n);
b.scan(), w.scan(), bw.scan();
if (abs (b.x - w.x) > abs (b.y - w.y) ) swap (b.x, b.y), swap (w.x, w.y), swap (bw.x, bw.y);
if (b.y < w.y) swap (b, w);
d = dis (b, w) - 1;
bl = br = b, wl = wr = w;
//b.print(),w.print(),bw.print(),printf("\n");
for (st = 0; st < (d + 1) / 2 && fail (bl) *fail (br) > 0 && fail (wl) *fail (wr) > 0; st++)
{
if (bl.x > 1 && w.x - bl.x + 1 < bl.y - w.y) bl.x--;
else if (w.x - bl.x + 1 > bl.y - w.y) bl.x++;
if (br.x < n && br.x - w.x + 1 < br.y - w.y) br.x++;
else if (br.x - w.x + 1 > br.y - w.y) br.x--;
bl.y--, br.y--;
if (wl.x > 1 && b.x - wl.x + 1 < b.y - wl.y) wl.x--;
else if (b.x - wl.x + 1 > b.y - wl.y) wl.x++;
if (wr.x < n && wr.x - b.x + 1 < b.y - wr.y) wr.x++;
else if (wr.x - b.x + 1 > b.y - wr.y) wr.x--;
wl.y++, wr.y++;
//bl.print(),br.print(),wl.print(),wr.print();
}
ans = (st < (d + 1) / 2);
printf ("%s\n%d\n", res[ans], ans ? st : d);
return 0;
}