搜索--广搜--最短路径长度--最短路径路径--最短路径最小字典序
抓住那头牛
农夫约翰被通知,他的一只奶牛逃逸了!所以他决定,马上出发,尽快把那只奶牛抓回来.
他们都站在数轴上.约翰在N(0≤N≤100000)处,奶牛在K(0≤K≤100000)处.约翰有
两种办法移动,步行和瞬移:步行每秒种可以让约翰从x处走到x+1或x-1处;而瞬移则可让他在1秒内从x处消失,在2x处出现.然而那只逃逸的奶牛,悲剧地没有发现自己的处境多么糟糕,正站在那儿一动不动.
那么,约翰需要多少时间抓住那只牛呢?
输入格式
* Line 1: Two space-separated integers: N and K
仅有两个整数N和K.
输出格式
* Line 1: The least amount of time, in minutes, it takes for Farmer John to catch the fugitive cow.
最短的时间.
样例
输入样例:
5 17
Farmer John starts at point 5 and the fugitive cow is at point 17.
输出样例:
4
OUTPUT DETAILS:
The fastest way for Farmer John to reach the fugitive cow is to
move along the following path: 5-10-9-18-17, which takes 4 minutes.
广搜 - -队列
每次取队头元素出队列,对于该队头节点,可能就是要求的节点,成功,退出;也可能不是,不是的话,利用该队头元素扩展与该节点有边相连且没有被访问的节点,将新的节点入队 ,直到队为空,所有图中相连的节点都被访问过。
devC++
//#include
#include
#include
#include
#include
#include
#include
#include
#include
迷宫问题
迷宫问题
Time Limit: 1000MS Memory Limit: 65536K
Description
定义一个二维数组:
int maze[5][5] = {
0, 1, 0, 0, 0,
0, 1, 0, 1, 0,
0, 0, 0, 0, 0,
0, 1, 1, 1, 0,
0, 0, 0, 1, 0,
};
它表示一个迷宫,其中的1表示墙壁,0表示可以走的路,只能横着走或竖着走,不能斜着走,要求编程序找出从左上角到右下角的最短路线。
Input
一个5 × 5的二维数组,表示一个迷宫。数据保证有唯一解。
Output
左上角到右下角的最短路径,格式如样例所示。
Sample Input
0 1 0 0 0
0 1 0 1 0
0 0 0 0 0
0 1 1 1 0
0 0 0 1 0
Sample Output
(0, 0)
(1, 0)
(2, 0)
(2, 1)
(2, 2)
(2, 3)
(2, 4)
(3, 4)
(4, 4)
//#include
#include
#include
#include
#include
#include
#include
#include
#include
最短路径问题
三行代码
floyd
小蓝学习了最短路径之后特别高兴,他定义了一个特别的图,希望找到图中的最短路径。
小蓝的图由2021 个结点组成,依次编号1 至2021。
对于两个不同的结点a, b,如果a 和b 的差的绝对值大于21,则两个结点之间没有边相连;
如果a 和b 的差的绝对值小于等于21,则两个点之间有一条长度为a 和b 的最小公倍数的无向边相连。
例如:结点1 和结点23 之间没有边相连;结点3 和结点24 之间有一条无向边,长度为24;
结点15 和结点25 之间有一条无向边,长度为75。
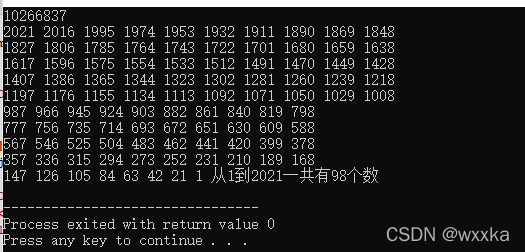
请计算,结点1 和结点2021 之间的最短路径长度是多少。
提示:建议使用计算机编程解决问题
最短路径模板
dijkstra从点A到终点K的最短路径长度,所有点构成的集合U,分为两类,一类是已经确定的最短路径的点集合V,一类是还没有确定最短路径的点集合U-V,这两种点可以用visited标记数组进行标记--初始,只有一个点A在V中,记录最短路径长度是0---每次,枚举所有的U-V的点,将到V中最短的点加入,更新最短路径长度,直到加入的点是K,中间要用数组存储每个点的直接前驱便于输出最短路径
//#include
#include
#include
#include
#include
#include
#include
#include
#include
floyd则是三重循环,枚举两个点(路径的两端),再在路径中间枚举所有点,找最短路径(可以看作动态规划)--暴力
for(int k = 1;k <= n;k++)//在最内层也可以
for(int i = 1;i <= n;i++)
for(int j = 1;j <= n;j++)
if(dis[i][j]>dis[i][k]+dis[k][j])
{dis[i][j] = dis[i][k]+dis[k][j];//path[i][j] = k;//记录路径数组}
#include
#include
using namespace std;
const int MAX = 1e9;
int mp[2025][2025];
int __gcd(int a, int b) {
while (a != b) {
if (a > b)
a = a - b;
else
b = b - a;
}
return a;
}
int main() {
for (int i = 1; i <= 2021; i++)
for (int j = 1; j <= 2021; j++)
{
if (i == j)
mp[i][j] = MAX;
else
if (abs(i - j) <= 21)
mp[i][j] = i * j / __gcd(i, j);
else
mp[i][j] = MAX;
}
for(int i = 1;i <= 2021;i++)
for(int j = 1;j <= 2021;j++)
for (int k = 1; k <= 2021; k++)
{
if (mp[i][j] > mp[i][k] + mp[k][j])
mp[i][j] = mp[i][k] + mp[k][j];
}
cout << mp[1][2021] << endl;
return 0;
}
蓝桥学院由21 栋教学楼组成,教学楼编号1 到21。
对于两栋教学楼a 和b,当a 和b 互质时,a 和b 之间有一条走廊直接相连,两个方向皆可通行,否则没有直接连接的走廊。
小蓝现在在第一栋教学楼,他想要访问每栋教学楼正好一次,最终回到第一栋教学楼(即走一条哈密尔顿回路),请问他有多少种不同的访问方案?
两个访问方案不同是指存在某个i,小蓝在两个访问方法中访问完教学楼i 后访问了不同的教学楼。
提示:建议使用计算机编程解决问题。
#include
#include
#include
using namespace std;
const int maxn = 21;
const int maxs = 1 << maxn;
typedef long long ll;
int N = 21;
ll dp[maxs + 100][maxn + 1];//dp[i][j],i存状态,j存当前点的序号
int g[maxn + 5][maxn + 5];//存图
int __gcd(int a, int b) {
while (a != b) {
if (a > b)
a = a - b;
else
b = b - a;
}
return a;
}
ll dfs(int state, int pos) {
//当前状态是state(state存储的是从1到pos(假设已经走了第pos位置)之后所有点的状态)
//当前状态的路径是从1经若干点走到点pos了,本次要处理的是第pos位置
if (dp[state][pos] != -1)return dp[state][pos];//一定要用到存储的状态!!!
ll res = 0;
for (int i = 1; i < N; i++) {//找本次pos位置的上一个位置状态,状态转换
if (((state >> i) & 1) == 0)continue;//第i个点没走过--不是上一个状态
//是上一个状态
if (g[i][pos] == 1) {//要有边才能转换
//改变state中存的pos的上一个点i的状态,状态转移--大状态变成小状态
dp[state - (1 << pos)][i] = dfs(state - (1 << pos), i);
res += dp[state - (1 << pos)][i];//不要直接用dp[state][pos]加因为初值是-1!!
}
}
return dp[state][pos] = res;
}
int main()
{
memset(dp, -1, sizeof dp);
for (int i = 1; i <= N; i++) {
for (int j = i; j <= N; j++) {
if (__gcd(i, j) == 1)g[i - 1][j - 1] = 1, g[j - 1][i - 1] = 1;//1到N映射为0到N-1
}
}
//从1走到任何一个点,都是可以的,方案数是1,状态是1<

//#include
#include
#include
#include
#include
#include
#include
#include
#include
枚举三个数,满足一定条件
小蓝有一个超大的仓库,可以摆放很多货物。
现在,小蓝有n 箱货物要摆放在仓库,每箱货物都是规则的正方体。
小蓝规定了长、宽、高三个互相垂直的方向,每箱货物的边都必须严格平行于长、宽、高。
小蓝希望所有的货物最终摆成一个大的立方体。即在长、宽、高的方向上分别堆L、W、H 的货物,满足n = L × W × H。
给定n,请问有多少种堆放货物的方案满足要求。
例如,当n = 4 时,有以下6 种方案:1×1×4、1×2×2、1×4×1、2×1×2、2×2×1、4×1×1。
请问,当n = 2021041820210418 (注意有16 位数字)时,总共有多少种
方案?
提示:建议使用计算机编程解决问题。
#include
#include
#include
using namespace std;
const int MAX = 1e9;
const long long n = 2021041820210418;
vector v;//存储所有因数
int main() {
for(int i = 1;i<=sqrt(n);i++)
if (n % i == 0)
{
v.push_back(i);
v.push_back(n / i);
}
long long ans = 0;
int size = v.size();
for (int i = 0; i < size; i++)
for (int j = 0; j < size; j++)
if (n % (v[i] * v[j]) == 0)
ans++;
cout << ans;
return 0;
}
枚举三个数,满足一定条件
问题描述
众所周知,小葱同学擅长计算,尤其擅长计算一个数是否是另外一个数的倍数。但小葱只擅长两个数的情况,当有很多个数之后就会比较苦恼。现在小葱给了你 n 个数,希望你从这 n 个数中找到三个数,使得这三个数的和是 K 的倍数,且这个和最大。数据保证一定有解。
输入格式
从标准输入读入数据。
第一行包括 2 个正整数 n, K。
第二行 n 个正整数,代表给定的 n 个数。
输出格式
输出到标准输出。
输出一行一个整数代表所求的和。
样例入
4 3
1 2 3 4
样例输出
9
样例说明
选择2、3、4。
数据约定
对于 30% 的数据,n <= 100。
对于 60% 的数据,n <= 1000。
对于另外 20% 的数据,K <= 10。
对于 100% 的数据,1 <= n <= 10^5, 1 <= K <= 10^3,给定的 n 个数均不超过 10^8。
资源约定:
峰值内存消耗(含虚拟机) < 256M
CPU消耗 < 1000ms
请严格按要求输出,不要画蛇添足地打印类似:“请您输入...” 的多余内容。
注意:
main函数需要返回0;
只使用ANSI C/ANSI C++ 标准;
不要调用依赖于编译环境或操作系统的特殊函数。
所有依赖的函数必须明确地在源文件中 #include
不能通过工程设置而省略常用头文件。
提交程序时,注意选择所期望的语言类型和编译器类型。
#include
#include
#include
#include
#include
#include
#include
#include
枚举三个数,满足一定条件
到x星球旅行的游客都被发给一个整数,作为游客编号。
x星的国王有个怪癖,他只喜欢数字3,5和7。
国王规定,游客的编号如果只含有因子:3,5,7,就可以获得一份奖品。
前10个幸运数字是:3 5 7 9 15 21 25 27 35 45,因而第11个幸运数字是:49
小明领到了一个幸运数字 59084709587505。
去领奖的时候,人家要求他准确说出这是第几个幸运数字,否则领不到奖品。
请你帮小明计算一下,59084709587505是第几个幸运数字。
#include
#include
#include
#include
#include
#include
#include
#include
思维题
如下的10行数据,每行有10个整数,请你求出它们的乘积的末尾有多少个零?
5650 4542 3554 473 946 4114 3871 9073 90 4329
2758 7949 6113 5659 5245 7432 3051 4434 6704 3594
9937 1173 6866 3397 4759 7557 3070 2287 1453 9899
1486 5722 3135 1170 4014 5510 5120 729 2880 9019
2049 698 4582 4346 4427 646 9742 7340 1230 7683
5693 7015 6887 7381 4172 4341 2909 2027 7355 5649
6701 6645 1671 5978 2704 9926 295 3125 3878 6785
2066 4247 4800 1578 6652 4616 1113 6205 3264 2915
3966 5291 2904 1285 2193 1428 2265 8730 9436 7074
689 5510 8243 6114 337 4096 8199 7313 3685 211
一开始,用高精度计算,暴力求解
代码如下
//#include
#include
#include
#include
#include
#include
#include
#include
#include
10的因数是1,2,5,10,只要有成对的因数2-5,就会有10,代码如下
#include
#include
#include
#include
#include
#include
#include
#include
答案是31
四平方和
四平方和定理,又称为拉格朗日定理:
每个正整数都可以表示为至多4个正整数的平方和。
如果把0包括进去,就正好可以表示为4个数的平方和。
比如:
5 = 0^2 + 0^2 + 1^2 + 2^2
7 = 1^2 + 1^2 + 1^2 + 2^2
(^符号表示乘方的意思)
对于一个给定的正整数,可能存在多种平方和的表示法。
要求你对4个数排序:
0 <= a <= b <= c <= d
并对所有的可能表示法按 a,b,c,d 为联合主键升序排列,最后输出第一个表示法
程序输入为一个正整数N (N<5000000)
要求输出4个非负整数,按从小到大排序,中间用空格分开
例如,输入:
5
则程序应该输出:
0 0 1 2
再例如,输入:
12
则程序应该输出:
0 2 2 2
再例如,输入:
773535
则程序应该输出:
1 1 267 838
资源约定:
峰值内存消耗 < 256M
CPU消耗 < 3000ms
请严格按要求输出,不要画蛇添足地打印类似:“请您输入...” 的多余内容。
所有代码放在同一个源文件中,调试通过后,拷贝提交该源码。
注意: main函数需要返回0
注意: 只使用ANSI C/ANSI C++ 标准,不要调用依赖于编译环境或操作系统的特殊函数。
注意: 所有依赖的函数必须明确地在源文件中 #include , 不能通过工程设置而省略常用头文件。
提交时,注意选择所期望的编译器类型。
暴力题,枚举三个数即可,第四个数不要枚举
#include
#include
#include
#include
using namespace std;
int a[10];
int main(){
int n;
while(scanf("%d",&n)!=EOF){
int q = sqrt(n);
int flag = 0;
for(int i = 0;i <= q;i++)
{
for(int j = i;j <= q;j++)
{
for(int k = j;k <= q;k++)
{
int tmp = n - i*i-j*j-k*k;
int sqrtmp = sqrt(tmp);
if(sqrtmp*sqrtmp == tmp)
{
flag = 1;
cout<
dfs剪枝--恢复现场

//#include
#include
#include
#include
#include
#include
#include
#include
#include
盾神与困难数独
问题描述
有一天,盾神接触到了风靡世界的小游戏——数独!!!盾神非常感兴趣,不惜翘课用了一天的时间把数独玩得出神入化!!!于是他要过来考考你。经过“盾神与简单数独”的磨练后,你会做9*9的了。
输入格式
输入为9*9的矩阵,如果第i行第j列为0,则该格子未填数;否则该格子已经有数。
输出格式
输出为1个9*9的矩阵,表示字典序最小的方案。如无解则输出NO。
矩阵大小关系的定义:第一关键字为a[1][1],第二关键字为a[1][2],……第四关键字为a[1][4],第五关键字为a[2][1],以此类推。矩阵A小于矩阵B,当且仅当存在k,A和B的前k-1个关键字的值都相等,而A的第k个关键字的值小于B的第k个关键字的值。矩阵A等于矩阵B,当且仅当A小于B和B小于A都不成立。
字典序升序的定义:在矩阵序列a中,对于任意的i<=j,有a[i]<=a[j]。
样例输入
1 2 3 4 5 6 7 8 9
2 0 0 0 0 0 0 0 0
3 0 0 0 0 0 0 0 0
4 0 0 0 0 0 0 0 0
5 0 0 0 0 0 0 0 0
6 0 0 0 0 0 0 0 0
7 0 0 0 0 0 0 0 0
8 0 0 0 0 0 0 0 0
9 0 0 0 0 0 0 0 0
样例输出
NO
样例输入
1 2 3 4 5 6 7 8 9
0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0
样例输出
1 2 3 4 5 6 7 8 9
4 5 6 7 8 9 1 2 3
7 8 9 1 2 3 4 5 6
2 1 4 3 6 5 8 9 7
3 6 5 8 9 7 2 1 4
8 9 7 2 1 4 3 6 5
5 3 1 6 4 2 9 7 8
6 4 2 9 7 8 5 3 1
9 7 8 5 3 1 6 4 2
数据规模和约定
矩阵中所有数的值为0到9。
补充一个常识:数独定义
数独(shù dú)是源自18世纪瑞士的一种数学游戏。是一种运用纸、笔进行演算的逻辑游戏。玩家需要根据9×9盘面上的已知数字,推理出所有剩余空格的数字,并满足每一行、每一列、每一个粗线宫(3*3)内的数字均含1-9,不重复 。
数独盘面是个九宫,每一宫又分为九个小格。在这八十一格中给出一定的已知数字和解题条件,利用逻辑和推理,在其他的空格上填入1-9的数字。使1-9每个数字在每一行、每一列和每一宫中都只出现一次,所以又称“九宫格”。
大致思路
每个3*3的粗线宫都含数字1-9,dfs,判断每行每列是否也满足1-9
上面的思路是错误的,不需要对每一个3*3的粗线格进行dfs,只要把3*3的粗线格的看作和行列一样的地位即可,就是判重
代码如下
//#include
#include
#include
#include
#include
#include
#include
#include
#include
分析上面的代码,这实际上是利用dfs来找一条路径----之前都是利用bfs进行最小字典序路径的搜索。根据上面的代码,可以看出,利用dfs进行字典序最小情况搜索时,具体操作如下, 此时,dfs时,我们设置返回值来表示当前是否找到了路径,找到了即返回,
//下一次搜索
if(dfs(num+1))
return 1;//这和以前不一样?
//原因:这是在找路,找第一条路 ,找到了就立刻返回
一般情况下,这里的话是dfs(num+1));在这里,这里找到了一条路就返回,不进行深搜,停止。
此外,这里,由num转化为row和col和groupIndex,这是较为常规的,这个思路可以借鉴二维数组转化为一维数组,int a[3][4],那么a[i][j]就是数组a中的第4*(i-1)+j -1个数。 同理,对于数组中第m个数,对应a[m/4][m%4]。
下面再给一例:
剪邮票
如下图, 有12张连在一起的12生肖的邮票。现在你要从中剪下5张来,要求必须是连着的。(仅仅连接一个角不算相连)

比如,下面两张图中,粉红色所示部分就是合格的剪取。
请你计算,一共有多少种不同的剪取方法。
分析:这道题中,我们每次从12个数中找5个数,利用二进制状态压缩(1表示选了,0表示没选),不过,需要将这个状态转化为这个数组里的数是否被选到了。
下面的代码是错误的
//#include
#include
#include
#include
#include
#include
#include
#include
#include
正确的代码如下,结果是116
//#include
#include
#include
#include
#include
#include
#include
#include
#include
正确代码或者如下
//#include
#include
#include
#include
#include
#include
#include
#include
#include
D. 大胖子走迷宫
【问题描述】
小明是个大胖子,或者说是个大大胖子,如果说正常人占用 1 × 1 的面积,小明要占用 5 × 5 的面积。
由于小明太胖了,所以他行动起来很不方便。当玩一些游戏时,小明相比小伙伴就吃亏很多。
小明的朋友们制定了一个计划,帮助小明减肥。计划的主要内容是带小明玩一些游戏,让小明在游戏中运动消耗脂肪。走迷宫是计划中的重要环节。
朋友们设计了一个迷宫,迷宫可以看成是一个由 n x n 个方降组成的方阵,正常人每次占用方阵中 1 × 1 的区域,而小明要占用 5 × 5 的区域。小明的位置定义为小明最正中的一个方格。迷宫四周都有障碍物。
为了方便小明,朋友们把迷宫的起点设置在了第 3 行第 3 列,终点设置在了第 n - 2 行第 n - 2 列。
小明在时刻 0 出发,每单位时间可以向当前位置的上、下、左、右移动单位 1 的距离,也可以停留在原地不动。小明走迷宫走得很辛苦,如果他在迷宫里面待的时间很长,则由于消耗了很多脂肪,他会在时刻 k 变成一个胖子,只占用 3 × 3 的区域。如果待的时间更长,他会在时刻 2k 变成一个正常人,只占用 1 × 1 的区域。注意,当小明变瘦时迷宫的起点和终点不变。
请问,小明最少多长时间能走到迷宫的终点。注意,小明走到终点时可能变瘦了也可能没有变瘦。
【输入形式】
输入的第一行包含两个整数 n,k。
接下来 n 行,每行一个由 n 个字符组成的字符串,字符为 + 表示为空地,字符为 * 表示为阻碍物。
【输出形式】
输出一个整数,表示答案。
【样例输入】
9 5
+++++++++
+++++++++
+++++++++
+++++++++
+++++++++
***+*****
+++++++++
+++++++++
+++++++++
【样例输出】
16
【评分标准】
对于 30% 的评测用例,1 ≤ n ≤ 50。
对于 60% 的评测用例,1 ≤ n ≤ 100。
对于所有评测用例,1 ≤ n ≤ 300,1 ≤ k ≤ 1000。
90/100代码
//#include
#include
#include
#include
#include
#include
#include
#include
#include
经检验,mque数组大小开到maxn*maxn*150即可100/100
思考:
模拟+bfs板子
胖子走迷宫,模拟时想象一个方格在移动,方格是5*5或者3*3或者1*1,不要以为是一个5*1或者3*1的矩形在移动;
每一步,能走则尽量走,实在走不了的话,就等---这是核心思路,有点贪心的味道
译成代码,能走,就是说,下一步合法,下一步合法就是说,下一步的坐标满足方格在迷宫中(不出界),方格内部没有障碍物(有障碍物胖子怎么走进去),同时,下一步必须要之前没有走过(走过再走就不合适了)
走和走不了是两种情况,上面的代码可以优化,但是,鉴于这两种情况混在一起用flag进行转换有时会出错,我上面的代码没有用flag联系,
int rr;
if (s.steps < k)rr = 2;
if (s.steps >= k && s.steps < k * 2) rr = 1;
if (s.steps >= 2 * k)rr = 0;
for (int i = 0; i < 4; i++) {
int ax = s.x + dx[i];
int ay = s.y + dy[i];
if (check(ax, ay, rr) && !visited[ax][ay]) {
mque[tail++] = fat(ax, ay, s.steps + 1);
visited[ax][ay] = 1;
}
}
//怎么写走不了的情况 -模拟走的所有可能-走不了的反面是有一条路可以走
int flag = 1;//默认走不了--flag是1表示走不了
for (int i = 0; i < 4; i++) {
int ax = s.x + dx[i];
int ay = s.y + dy[i];
if (check(ax, ay, rr)&&!visited[ax][ay]) {
flag = 0;
break;
}
}
if (flag) {//走不了,等待
mque[tail++] = fat(s.x, s.y, s.steps + 1);
}
上面这段代码可以改为下面这串吗
int rr;
int flag = 1;//默认走不了--flag是1表示走不了
if (s.steps < k)rr = 2;
if (s.steps >= k && s.steps < k * 2) rr = 1;
if (s.steps >= 2 * k)rr = 0;
for (int i = 0; i < 4; i++) {
int ax = s.x + dx[i];
int ay = s.y + dy[i];
if (check(ax, ay, rr) && !visited[ax][ay]) {
mque[tail++] = fat(ax, ay, s.steps + 1);
visited[ax][ay] = 1;
flag = 0;
}
}
//怎么写走不了的情况 -模拟走的所有可能-走不了的反面是有一条路可以走
//for (int i = 0; i < 4; i++) {
//int ax = s.x + dx[i];
//int ay = s.y + dy[i];
//if (check(ax, ay, rr)&&!visited[ax][ay]) {
//flag = 0;
//break;
//}
//}
if (flag) {//走不了,等待
mque[tail++] = fat(s.x, s.y, s.steps + 1);
}
上面这段代码是不对的,实现不了走和不走这两种状态的转换,最后导致代码逻辑和自己想的逻辑不一致的情况出现,还是分开写
经思考,我的代码思路实际上是,对每一步,都进行等待操作(出某个元素前进这个元素坐标的步数+1这种情况到队列中)和走操作(如果可以走的话),对内存消耗大
对于上面的代码,注意到,只要变成1*1的胖子后,肯定不需要等待,即
if(rr!=0)
mque[tail++] = fat(r.x,r.y,r.steps+1);
这样,对于mque,需要的大小可以减少很多,经检验,减少到maxn*maxn*10就可以了(比这更小的没有测试,没必要再试了)
具体代码如下
//#include
#include
#include
#include
#include
#include
#include
#include
#include
学霸的作业
问题描述
学霸抢走了大家的作业,班长为了帮同学们找回 作业,决定去找学霸决斗。但学霸为了不要别人打扰,住在一个城堡里,城堡外面是一个二维的格子迷宫,要进城堡必须得先通过迷宫。因为班长还有妹子要陪,磨 刀不误砍柴功,他为了节约时间,从线人那里搞到了迷宫的地图,准备提前计算最短的路线。可是他现在正向妹子解释这件事情,于是就委托你帮他找一条最短的路线。
输入格式
第一行两个整数n, m,为迷宫的长宽。
接下来n行,每行m个数,数之间没有间隔,为0或1中的一个。0表示这个格子可以通过,1表示不可以。假设你现在已经在迷宫坐标(1,1)的地方,即 左上角,迷宫的出口在(n,m)。每次移动时只能向上下左右4个方向移动到另外一个可以通过的格子里,每次移动算一步。数据保证(1,1),(n,m)可 以通过。
输出格式
第一行一个数为需要的最少步数K。
第二行K个字符,每个字符∈{U,D,L,R},分别表示上下左右。如果有多条长度相同的最短路径,选择在此表示方法下字典序最小的一个。
样例输入
Input Sample 1:
3 3
001
100
110
Input Sample 2:
3 3
000
000
000
样例输出
Output Sample 1:
4
RDRD
Output Sample 2:
4
DDRR
数据规模和约定
有20%的数据满足:1<=n,m<=10
有50%的数据满足:1<=n,m<=50
有100%的数据满足:1<=n,m<=500。
广搜+字典序
记录广搜中的信息,可以将需要的信息,如点的坐标(搜索时需要,用来判断是否可以过去是否访问过是否过界),最短路径长度,上一个节点在队列中的位置,从上个节点走到该点的行走方向,放到一个struct中即可,队列每次拿出一个,按照字典序来扩展与拿出的点的相连的点,扩展的点加到队列中(同时tail指针后移),全部拓展后head指针++,表示该点出队列
了解字典序是什么即可,加了一个字典序,就是固定了遍历顺序,即在遍历时要按照字典序从小到大的顺序进行遍历就行了----遍历就是暴力搜索----此处有四个方向,类比四重循环,每层循环要求循环1-9,要求输出按照字典序从小到大输出,则每层按照1-9的顺序遍历即可。
记录最短路径,用到上面说的 上一个节点在队列中的位置,从上个节点走到该点的行走方向,即可。
自己编写的代码
经历的错误:输入的顺序是n和m,不是m和n,每行输入的是字符串,可以用C中char*或者C++中string,还有,由于是字符,所以判断能不能通过的时候,要么统一用字符‘0’与‘0’比较,要么统一化为数字比较,否则会出错。
获得path路径的一种写法
//#include
#include
#include
#include
#include
#include
#include
#include
#include
获得path路径的另一种写法
//#include
#include
#include
#include
#include
#include
#include
#include
#include
并查集应用:
C国由n个小岛组成,为了方便小岛之间联络,C国在小岛间建立了m座大桥,每座大桥连接两座小岛。两个小岛间可能存在多座桥连接。然而,由于海水冲刷,有一些大桥面临着不能使用的危险。
如果两个小岛间的所有大桥都不能使用,则这两座小岛就不能直接到达了。然而,只要这两座小岛的居民能通过其他的桥或者其他的小岛互相到达,他们就会安然无事。但是,如果前一天两个小岛之间还有方法可以到达,后一天却不能到达了,居民们就会一起抗议。
现在C国的国王已经知道了每座桥能使用的天数,超过这个天数就不能使用了。现在他想知道居民们会有多少天进行抗议。
样例说明
第一天后2和3之间的桥不能使用,不影响。
第二天后1和2之间,以及1和3之间的桥不能使用,居民们会抗议。
第三天后3和4之间的桥不能使用,居民们会抗议。
数据规模和约定
对于30%的数据,1<=n<=20,1<=m<=100;
对于50%的数据,1<=n<=500,1<=m<=10000;
对于100%的数据,1<=n<=10000,1<=m<=100000,1<=a, b<=n, 1<=t<=100000。
输入
输入的第一行包含两个整数n, m,分别表示小岛的个数和桥的数量。
接下来m行,每行三个整数a, b, t,分别表示该座桥连接a号和b号两个小岛,能使用t天。小岛的编号从1开始递增。
输出
输出一个整数,表示居民们会抗议的天数。
样例输入
4 4
1 2 2
1 3 2
2 3 1
3 4 3
样例输出
2
D. CCF 201703-4 地铁修建
【问题描述】
A市有n个交通枢纽,其中1号和n号非常重要,为了加强运输能力,A市决定在1号到n号枢纽间修建一条地铁。
地铁由很多段隧道组成,每段隧道连接两个交通枢纽。经过勘探,有m段隧道作为候选,两个交通枢纽之间最多只有一条候选的隧道,没有隧道两端连接着同一个交通枢纽。
现在有n家隧道施工的公司,每段候选的隧道只能由一个公司施工,每家公司施工需要的天数一致。而每家公司最多只能修建一条候选隧道。所有公司同时开始施工。
作为项目负责人,你获得了候选隧道的信息,现在你可以按自己的想法选择一部分隧道进行施工,请问修建整条地铁最少需要多少天。
【输入形式】
输入的第一行包含两个整数n, m,用一个空格分隔,分别表示交通枢纽的数量和候选隧道的数量。
第2行到第m+1行,每行包含三个整数a, b, c,表示枢纽a和枢纽b之间可以修建一条隧道,需要的时间为c天。
【输出形式】
输出一个整数,修建整条地铁线路最少需要的天数。
【样例输入】
6 6
1 2 4
2 3 4
3 6 7
1 4 2
4 5 5
5 6 6
【样例输出】
6
【样例说明】
可以修建的线路有两种。
第一种经过的枢纽依次为1, 2, 3, 6,所需要的时间分别是4, 4, 7,则整条地铁线需要7天修完;
第二种经过的枢纽依次为1, 4, 5, 6,所需要的时间分别是2, 5, 6,则整条地铁线需要6天修完。
第二种方案所用的天数更少。
【评分标准】
对于20%的评测用例,1 ≤ n ≤ 10,1 ≤ m ≤ 20;
对于40%的评测用例,1 ≤ n ≤ 100,1 ≤ m ≤ 1000;
对于60%的评测用例,1 ≤ n ≤ 1000,1 ≤ m ≤ 10000,1 ≤ c ≤ 1000;
对于80%的评测用例,1 ≤ n ≤ 10000,1 ≤ m ≤ 100000;
对于100%的评测用例,1 ≤ n ≤ 100000,1 ≤ m ≤ 200000,1 ≤ a, b ≤ n,1 ≤ c ≤ 1000000。
所有评测用例保证在所有候选隧道都修通时1号枢纽可以通过隧道到达其他所有枢纽。
初步代码dijkstra
//#include
#include
#include
#include
#include
#include
#include
#include
#include
运行结果

超时超内存
代码问题,无向图,i与j之间的路是无向的
下面代码错误
for (int i = 1; i <= m; i++) {
int a, b, c;
scanf("%d %d %d", &a, &b, &c);
mp[{a, b}] = c;
}
改为下面的
for (int i = 1; i <= m; i++) {
int a, b, c;
scanf("%d %d %d", &a, &b, &c);
mp[{a, b}] = c;
mp[{b, a}] = c;
}
结果如下

目前不对本题作进一步探究
E. CCF 201609-4 交通规划
【问题描述】
G国国王来中国参观后,被中国的高速铁路深深的震撼,决定为自己的国家也建设一个高速铁路系统。
建设高速铁路投入非常大,为了节约建设成本,G国国王决定不新建铁路,而是将已有的铁路改造成高速铁路。现在,请你为G国国王提供一个方案,将现有的一部分铁路改造成高速铁路,使得任何两个城市间都可以通过高速铁路到达,而且从所有城市乘坐高速铁路到首都的最短路程和原来一样长。请你告诉G国国王在这些条件下最少要改造多长的铁路。
【输入形式】
输入的第一行包含两个整数n, m,分别表示G国城市的数量和城市间铁路的数量。所有的城市由1到n编号,首都为1号。
接下来m行,每行三个整数a, b, c,表示城市a和城市b之间有一条长度为c的双向铁路。这条铁路不会经过a和b以外的城市。
【输出形式】
输出一行,表示在满足条件的情况下最少要改造的铁路长度。
【样例输入】
4 5
1 2 4
1 3 5
2 3 2
2 4 3
3 4 2
【样例输出】
11
【样例说明】
对于20%的评测用例,1 ≤ n ≤ 10,1 ≤ m ≤ 50;
对于50%的评测用例,1 ≤ n ≤ 100,1 ≤ m ≤ 5000;
对于80%的评测用例,1 ≤ n ≤ 1000,1 ≤ m ≤ 50000;
对于100%的评测用例,1 ≤ n ≤ 10000,1 ≤ m ≤ 100000,1 ≤ a, b ≤ n,1 ≤ c ≤ 1000。输入保证每个城市都可以通过铁路达到首都。
【评分标准】
J. CCF 201604-2 俄罗斯方块
【问题描述】
俄罗斯方块是俄罗斯人阿列克谢·帕基特诺夫发明的一款休闲游戏。
游戏在一个15行10列的方格图上进行,方格图上的每一个格子可能已经放置了方块,或者没有放置方块。每一轮,都会有一个新的由4个小方块组成的板块从方格图的上方落下,玩家可以操作板块左右移动放到合适的位置,当板块中某一个方块的下边缘与方格图上的方块上边缘重合或者达到下边界时,板块不再移动,如果此时方格图的某一行全放满了方块,则该行被消除并得分。
在这个问题中,你需要写一个程序来模拟板块下落,你不需要处理玩家的操作,也不需要处理消行和得分。
具体的,给定一个初始的方格图,以及一个板块的形状和它下落的初始位置,你要给出最终的方格图。
【输入形式】
输入的前15行包含初始的方格图,每行包含10个数字,相邻的数字用空格分隔。如果一个数字是0,表示对应的方格中没有方块,如果数字是1,则表示初始的时候有方块。输入保证前4行中的数字都是0。
输入的第16至第19行包含新加入的板块的形状,每行包含4个数字,组成了板块图案,同样0表示没方块,1表示有方块。输入保证板块的图案中正好包含4个方块,且4个方块是连在一起的(准确的说,4个方块是四连通的,即给定的板块是俄罗斯方块的标准板块)。
第20行包含一个1到7之间的整数,表示板块图案最左边开始的时候是在方格图的哪一列中。注意,这里的板块图案指的是16至19行所输入的板块图案,如果板块图案的最左边一列全是0,则它的左边和实际所表示的板块的左边是不一致的(见样例)
【输出形式】
输出15行,每行10个数字,相邻的数字之间用一个空格分隔,表示板块下落后的方格图。注意,你不需要处理最终的消行。
【样例输入】
0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 1 0 0
0 0 0 0 0 0 1 0 0 0
0 0 0 0 0 0 1 0 0 0
1 1 1 0 0 0 1 1 1 1
0 0 0 0 1 0 0 0 0 0
0 0 0 0
0 1 1 1
0 0 0 1
0 0 0 0
3
【样例输出】
0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 1 0 0
0 0 0 0 0 0 1 0 0 0
0 0 0 0 0 0 1 0 0 0
1 1 1 1 1 1 1 1 1 1
0 0 0 0 1 1 0 0 0 0
![]()



