自动控制原理 - 1 绪论内容

注意：1.学习目标是掌握基本理论理解扎实，抓主要内容主要方法牢记扎实

2.学习理论的目的是为了应用，因此时刻结合应用角度与分享人角度去学习。

3.打完扎实基础后如果以后有什么不明白知识点回来补充与学习。

---

1 绪论内容1.1 自动控制系统的基本原理1.2 自动控制系统的分类1.3 自动控制系统的要求1.4 自动控制的发展史

1 绪论内容

1.1 自动控制系统的基本原理

什么是控制：使某个（某些）量按一定的规律变化，某个（某些）量称为被控制量。

自动控制: 在脱离人的直接干预下，利用控制装置，使被控对象按照预定的规律运行；

自动控制系统: 将被控的对象和实现控制功能的控制装置组合起来---称为自动控制系统。

被控对象 （也称被控过程、被控系统）：它可能是一个设备，多数由一些机器零件有机地组合在一起，

其作用是完成一种特定的操作。

被控参数（也称为系统输出）体现系统控制目的的物理量。（速度，距离、方位角度等）

控制参数：由控制器改变的量，对被控参数有较好的调节能力。（阀门开度、电枢电压等）

系统输入：作用于被控对象或系统输入端，并可使系统具有预定功能或预定输出的物理量。（给定温度，电位器滑杆位置）

扰动：一种对系统的输出量产生影响的信号。(水箱漏出水、负载等）

开环控制：输出量对输入量(控制作用)没有影响的系统。缺点：没有抵抗扰动的能力。

闭环控制：将输出量与参考输入量进行比较，并且将它们的偏差作为控制手段，以保持两者之间预定关系的

系统，也称为反馈控制系统。将输出量反送到输入端，与输入端形成偏差称之为反馈。控制系统中主要采用负反馈。

负反馈（输入量与抽出量相减）特点：反馈的加入，使偏差越来越小。使系统对参数不敏感。

正反馈（输入量与抽出量相互叠加）特点：反馈的加入，使偏差越来越大。（振荡发生器）

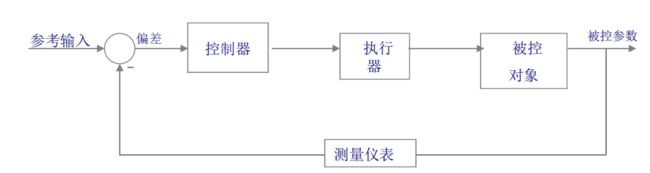
控制系统通常习惯用结构图来表示：方框代表功能模块；带箭头的线段：代表信号传递方向；典型的控制系统结构图如下。参考输入与测量仪表得到的被控参数进行误差运算，形成的误差信号经过控制器运算输出控制量，控制量通过执行器作用到被控对象去改变控制参数。

 

1.2 自动控制系统的分类

按输入信号的变化规律分：

定值控制：参考输入为一个恒定的值。如速度控制、液位控制等。

程序控制：参考输入为一个已知的时间函数。如热处理过程先升温后降温。

随动控制：参考输入为一个随机变化的函数。雷达天线跟踪系统等

按系统中传递信号的特点分

连续信号：系统中传递的信号都是时间轴上连续的信号。描述对象的数学模型是微分方程。

离散系统：系统中某一处或几处信号为脉冲序列或时间轴上不连续的信号，描述此类系统的数学模型为差分方 程。典型的如计算机控制系统。

按系统特点分

线性系统：组成系统的所有元件或子系统都是线性的。包括线性定常连续系统（线性微分方程描述它）与线性定常离散系统（线性差分方程描述它）。例如图示线性定常连续系统。

 

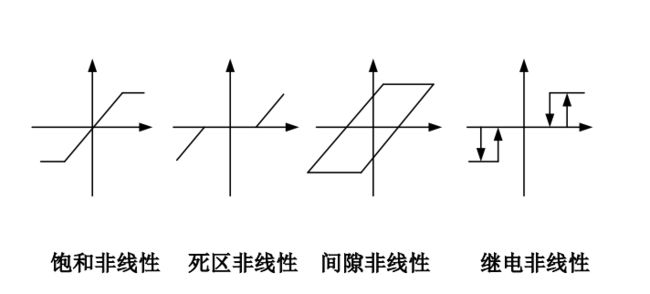
非线性系统：系统中至少有一个元件或子系统是非线性的。

 

按系统输入输出数量分

单输入单输出（经典控制理论）：如电动机速度控制系统

多输入多输出（现代控制理论）：如四旋翼系统

按系统功能分：温度控制、速度控制、位置控制。

按控制规律分：

古典控制系统（基于传递函数建立被控对象数学模型，根据根轨迹法与频域法分析法 来设计与分析控制器）

现代控制系统（基于状态空间描述对象数学模型，利用状态反馈设计控制器）

模糊控制系统（利用模糊理论设计控制器）。

神经网络控制系统（利用神经网络理论建立被控对象数学模型，设计控制器）。

模糊控制与神经网络控制属于智能控制范畴。

1.3 自动控制系统的要求

建立控制系统的目的：1保证系统输出具有控制输入指定的数值；2保证系统输出尽量不受扰动的影响

对系统的具体要求：

（1）系统稳定性：即恢复到平衡状态能力，不能等幅度震荡或震荡越来越大，是控制的最基本要求。

（2）系统动态快速性：即快速达到期望值，为工作高效要求。如汽车百米加速响应

（3）系统的稳态性：当被控制量由初始值变为另一个希望值时，某些控制系统会出现超调现象。即被控制量会超过希望值，并经过若干次摆动以后才达到希望值。

（4）准确性：如果要求被控制量由初始值变为另一个希望值时，在变化过程结束后，被控制量能够达到希望值，说明该系统具有很好的准确性。

以上四项对控制系统的要求可以归纳为“稳、快、平、准”四个字。其中，快速性和平稳性反映控制系统的动态品质；准确性反映反映控制系统的稳态精度；而稳定性则是控制系统能够正常工作的先决条件。

本课程的任务：研究一种方法（或理论）来指导构筑一个控制系统达到系统目标。具体做法是设计控制装置以达到系统的目的。

认识控制世界：即了解各种元器件或子系统的运动规律、动力学方程（即建立数学模型） ；了解某种控制器对系统输出的影响（即系统分析）。其中对应章节：第2章：自动控制系统的数学模型。第3章：自动控制系统的时域分析。第4章：自动控制系统的根轨迹分析。第5章：自动控制系统的频域分析。

改造控制世界：设计控制器（系统设计或系统综合） 对应第6章：自动控制系统的校正

1.4 自动控制的发展史

经典控制理论阶段1900-1950（以传递函数作为系统数学模型）：

麦克斯韦尔基于微分方程描述从理论上给出了它的稳定性条件。

劳斯与霍尔维茨分别独立给出了高阶线性系统的稳定性判据

李雅普诺夫给出了非线性系统的稳定性判据

柰奎斯特提出了负反馈系统的频率域稳定性判据。

伊文斯又进一步提出了属于经典方法的根轨迹设计法，它给出了系统参数变换与时域性能变化之间的关系

经典控制理论的分析方法为复数域方法,以传递函数作为系统数学模型，优点:可通过试验方法建立数学模型， 物理概念清晰。缺点:只适应单变量线性定常系统，对系统内部状态缺少了解。

现代控制理论阶段1920-now（以状态空间表达式为模型）：

1954年贝尔曼(R.Bellman)的动态规划理论；

1956年庞特里雅金(L.S.Pontryagin)的极大值原理

1960年卡尔曼（R.E.Kalman）提出多变量最优控制和最优滤波理论。

状态空间方法属于时域方法，其核心是最优化技术。它以状态空间描述（实质上是一阶微分或差分方程组）作

为数学模型，适应于多变量、非线性、时变系统

智能控制阶段：

智能控制依据人的思维方式和处理问题的技巧，解决那些目前需要人的智能才能解决的复杂的控制问题。被控对象的复杂性体现为:模型的不确定性，高度非线性，分布式的传感器和执行器，动态突变，多时间标度，复杂的信息模式，庞大的数据量，以及严格的特性指标等。环境的复杂性则表现为变化的不确定性和难以辨识。试图用传统的控制理论和方法去解决复杂的对象，复杂的环境和复杂的任务是不可能的。智能控制的方法包括模糊控制，神经元网络控制，专家控制等方法。