SIFT特征详细分析 上
一、介绍
特征的检测和匹配在许多计算机视觉应用中是一个重要的组成部分,例如无缝拼接,三维重建等。其中兴趣点特征是很重要的一类特征,而目前应用最广泛的兴趣点特征检测方法就是SIFT检测算法,该检测算法所得到的特征点不仅在位置上能够稳定识别,而且具有尺度不变性和旋转不变性。由于各大论坛以及该论文作者都只是给出matlab的实现算法,并未给出C++的版本,而且由于在SIFT的实现过程中有很多参数设置和细节上的优化处理,实现起来比较复杂。该程序使用主流的开源的OpenCV库函数给出了C++版本的SIFT特征检测算法,并结合样例,详细地描述了实现过程中的大部分细节。
二、算法描述
SIFT特征不只具有尺度不变性,即使改变旋转角度,图像亮度或拍摄视角,仍然能够得到好的检测效果。由于SIFT算法有很多操作,会令人不解,这里将整个算法分为多个部分:
1. 构建尺度空间
这是一个初始化操作,通过生成尺度空间来创建原始图像的多层表示以保证尺度不变性。
2. LoG近似
使用Laplacian of Gaussian能够很好地找到找到图像中的兴趣点,但是需要大量的计算量,所以使用创建更容易的表示来近似它。
3. 找到关键点
利用很快的近似,我们可以找到特征点,它们是Difference of Gaussian图像的极大极小值。
4. 除去不好的特征点
边界和低亮度区域是不好的特征点,除去它们以使得算法有效和鲁棒,在这里使用近似Harris Corner检测器。
5. 给特征点赋值一个方向
为每个特征点计算一个方向,依照这个方向做进一步的计算,这个操作有效地取消了方向的影响,使得算法具有旋转不变性。
6. 生成SIFT特征
最后,利用位置上的尺度和旋转不变性,能够生成一个表示,它能帮助唯一地识别特征。通过这个表示,我们可以很容易识别寻找的特征。
2.1创建尺度空间
真实世界的物体只在某一尺度下是有意义的。靠近的时候,我们能够看清楚的东西,可能远离的时候就不见了;带上眼睛能够看清楚的东西,可能脱下眼睛就看不见了。物体这种多尺度的性质是很常见的,并且尺度空间就是将这个性质用在数字图像中。
尺度空间
你是想看树叶还是整棵书?如果是树,就要有目的摆脱图像中的细节(像树叶,小枝等),当摆脱了这些细节,还要避免引入新的错误的细节。唯一的方法就是使用高斯模糊(在几个合理的假设下,这是经过数学证明的)。
|
所以为了创建一个尺度空间,我们可以利用原始的图像来逐渐生成模糊后的图像,下图显示了图像是如何摆脱细节的,如猫的胡须。
 |
在SIFT中的尺度空间
SIFT需要多组(octave)尺度空间,用第一幅图像逐渐生成一组模糊后的图像,然后将原始图像的尺寸缩小一半,再逐渐生成下一组模糊后的图像,以此类推。
 |
 |
|
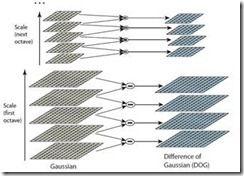
相同大小的图像形成一组尺度空间,上面有四组尺度空间,每组有5张图像,且这些图像通过增加尺度(模糊量)逐渐形成。
在SIFT算法的第一阶段,我们生成了原始图像的多组尺度空间,每个组的图像大小是前者的一半。在一组尺度空间中,图像使用高斯模糊操作被逐渐模糊。
实现细节
1. 组数和尺度数依赖于原始图像的大小,SIFT算法发明者建议将组数设为4,尺度数设为5是比较理想的。在实现中我们采用作者的建议。
2. 第一组的图像并不是直接使用原始图像,而是使用大小放大两倍并稍微模糊后的图像,这样可以多产生4倍的特征点。
3. 数学上,模糊指的是图像与高斯核的卷积,卷积后的图像是一个模糊的图像。
4.
 |
每个图像的模糊量是很重要的,假设一幅图像的模糊量是σ,那么下一幅图像的模糊量是k*σ,这里的k是一个常量。
|
这是我们程序中所使用的σ图表,在同一组中,下一幅图像比前一幅图像在σ上相差sqrt(2),即![]() 。
。
2.2 Laplacian of Gaussian的近似
在上一步,我们通过逐渐模糊图像,创建了图像的尺度空间。现在使用这些模糊的图像来生成另一类图像组Differece of Gaussain(DoG),这些DoG图像很适合在图像中找感兴趣的特征点。
Laplacian of Gaussian
Laplacian of Gaussian操作按下面进行,取一张图像将其模糊一点,并且计算它的二阶导数,这样可以定位图像中的边界和直角。这些边界和直角对于找到特征点是很有帮助的。但是二阶导数对噪音是非常敏感的,通过使用模糊操作平滑噪音,可以稳定了二阶导数。这个问题计算所有二阶导数需要大量的计算,所以使用近似操作。
|
Difference of Gaussian图像近似等于Laplacian of Gaussian,并且我们用一个简单的减法来替换计算量大的Laplacian操作,这些DoG图像是尺度不变的。
近似的好处
只是对图像进行Laplacain操作不够好,得到的图像还不是尺度不变的,因为它们还依赖于模糊量σ。高斯表达式的分母中有σ2项,它就是尺度,只有除去它,才能得到真正的尺度不变性。所以如果将Laplacian of Gaussain表示为![]() ,那么尺度不变的Laplacian of Gaussian就是
,那么尺度不变的Laplacian of Gaussian就是![]() ,但是所有这些都可以通过Difference of Gaussian操作来表示,并且通过证明这样的尺度不变操作可以产生更多可跟踪的特征点。
,但是所有这些都可以通过Difference of Gaussian操作来表示,并且通过证明这样的尺度不变操作可以产生更多可跟踪的特征点。 
|
实现细节
这里用一系列图像来说明这些difference of Gaussian是如何实现的,如图2.5所示。
在这一组图像中,对每两幅尺度相邻的图像做减法操作,就可以生成相应的DoG图像。每组图像中两个连续图像被选择,并用一幅图像减去另一幅图像,然后下一对图像也被选择,这个过程重复进行,并用于每一组图像。由于尺度数设为5,每组图像可以得到4幅DoG图像。这个DoG图像是尺度不变的Laplacian of Gaussian,它对于检测特征点是很有用的。