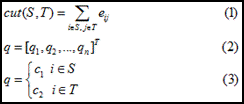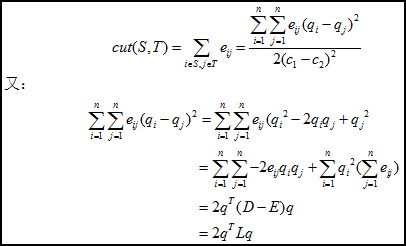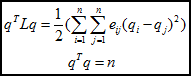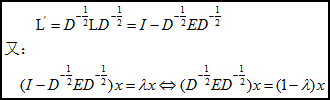谱聚类算法(Spectral Clustering)
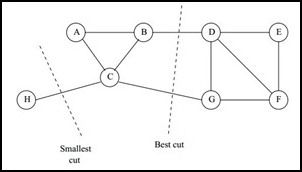
谱聚类(Spectral Clustering, SC)是一种基于图论的聚类方法——将带权无向图划分为两个或两个以上的最优子图,使子图内部尽量相似,而子图间距离尽量距离较远,以达到常见的聚类的目的。其中的最优是指最优目标函数不同,可以是割边最小分割——如图1的Smallest cut(如后文的Min cut), 也可以是分割规模差不多且割边最小的分割——如图1的Best cut(如后文的Normalized cut)。
图1 谱聚类无向图划分——Smallest cut和Best cut
这样,谱聚类能够识别任意形状的样本空间且收敛于全局最优解,其基本思想是利用样本数据的相似矩阵(拉普拉斯矩阵)进行特征分解后得到的特征向量进行聚类。
1 理论基础
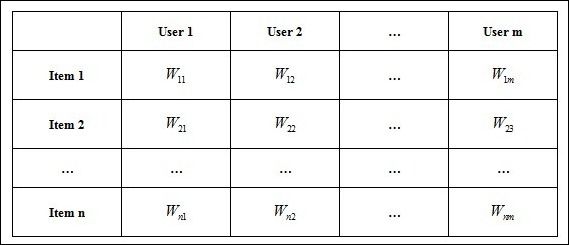
对于如下空间向量item-user matrix:
如果要将item做聚类,常常想到k-means聚类方法,复杂度为o(tknm),t为迭代次数,k为类的个数、n为item个数、m为空间向量特征数:
1 如果M足够大呢?
2 K的选取?
3 类的假设是凸球形的?
4 如果item是不同的实体呢?
5 Kmeans无可避免的局部最优收敛?
……
这些都使常见的聚类问题变得相当复杂。
1.1 图的表示
如果我们计算出item与item之间的相似度,便可以得到一个只有item的相似矩阵,进一步,将item看成了Graph(G)中Vertex(V),item之间的相似度看成G中的Edge(E),这样便得到我们常见的图的概念。
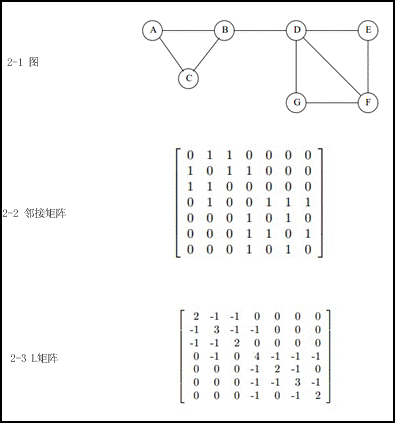
对于图的表示(如图2),常用的有:
邻接矩阵:E,eij表示vi和vi的边的权值,E为对称矩阵,对角线上元素为0,如图2-2。
Laplacian矩阵:L = D – E, 其中di (行或列元素的和),如图2-3。
1.2 特征值与L矩阵
先考虑一种最优化图像分割方法,以二分为例,将图cut为S和T两部分,等价于如下损失函数cut(S, T),如公式1所示,即最小(砍掉的边的加权和)。
假设二分成两类,S和T,用q(如公式2所示)表示分类情况,且q满足公式3的关系,用于类标识。
那么:
其中D为对角矩阵,行或列元素的和,L为拉普拉斯矩阵。
由:
有:
1、 L为对称半正定矩阵,保证所有特征值都大于等于0;
2、 L矩阵有唯一的0特征值,其对应的特征向量为1。
离散求解q很困难,如果将问题松弛化为连续实数值,由瑞利熵的性质知其二将你型的最小值就是L的特征值们(最小值,第二小值,......,最大值分别对应矩阵L的最小特征值,第二小特征值,......,最大特征值,且极值q相应的特征向量处取得,请参见瑞利熵(Rayleigh quotient))。
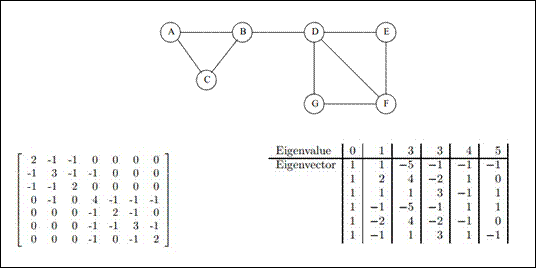
写到此,不得不对数学家们致敬,将cut(S,T),巧妙地转换成拉普拉斯矩阵特征值(向量)的问题,将离散的聚类问题,松弛为连续的特征向量,最小的系列特征向量对应着图最优的系列划分方法。剩下的仅是将松弛化的问题再离散化,即将特征向量再划分开,便可以得到相应的类别,如将图3中的最小特征向量,按正负划分,便得类{A,B,C}和类{D,E,F,G}。在K分类时,常将前K个特征向量,采用kmeans分类。
PS:
1、此处虽再次提到kmeans,但意义已经远非引入概念时的讨论的kmeans了,此处的kmeans,更多的是与ensemble learning相关,在此不述;
2、k与聚类个数并非要求相同,可从第4节的相关物理意义中意会;
3、在前k个特征向量中,第一列值完全相同(迭代算法计算特征向量时,值极其相近),kmeans时可以删除,同时也可以通过这一列来简易判断求解特征值(向量)方法是否正确,常常问题在于邻接矩阵不对称。
图3 图的L矩阵的特征值与特征向量
2 最优化方法
在kmeans等其它聚类方法中,很难刻划类的大小关系,局部最优解也是无法回避的漏病。当然这与kmeans的广泛使用相斥——原理简单。
2.1 Min cut方法
如2.2节的计算方法,最优目标函数如下的图cut方法:
计算方法,可直接由计算L的最小特征值(特征向量),求解。
2.2 Nomarlized cut方法
Normarlized cut,目标是同时考虑最小化cut边和划分平衡,以免像图1中的cut出一个单独的H。衡量子图大小的标准是:子图各个端点的Degree之和。
2.3 Ratio Cut 方法
Ratio cut的目标是同时考虑最小化cut边和划分平衡,以免像图1中的cut出一个单独的H。
最优目标函数为:
2.4 Normalized相似变换
归一化的L矩阵有:
因而L’的最小特征值与D-(1/2)E D-(1/2)的最大特征值对应。
而计算的L’相比计算L要稍具优势,在具体实用中,常以L’替代L,但是min cut和ratio cut不可以。
PS:这也是常常在人们的博客中,A说谱聚类为求最大K特征值(向量),B说谱聚类为求最小K个特征值(向量的原因)。
3 谱聚类步骤
第一步:数据准备,生成图的邻接矩阵;
第二步:归一化普拉斯矩阵;
第三步:生成最小的k个特征值和对应的特征向量;
第四步:将特征向量kmeans聚类(少量的特征向量);
4 谱聚类的物理意义
谱聚类中的矩阵:
可见不管是L、L’都与E联系特别大。如果将E看成一个高维向量空间,也能在一定程度上反映item之间的关系。将E直接kmeans聚类,得到的结果也能反映V的聚类特性,而谱聚类的引入L和L’是使得G的分割具有物理意义。
而且,如果E的item(即n)足够大,将难计算出它的kmeans,我们完全可以用PCA降维(仍为top的特征值与向量)。
上述对将E当成向量空间矩阵,直观地看符合我们的认知,但缺乏理论基础;而L(L’等)的引入,如第2节所述,使得计算具有理论基础,其前k个特征向量,也等价于对L(L’等)的降维。
因而聚类就是为图的划分找了理论基础,能达到降维的目的。
其中不少图出源于Mining of Massive Datasets,对于同仁们的布道授业,一并感谢。
推荐相关相关文档:Wen-Yen Chen, Yangqiu Song, Hongjie Bai, Chih-Jen Lin, Edward Y. Chang. Parallel Spectral Clustering in Distributed Systems.
via http://blog.csdn.net/pi9nc/article/details/12251247