【ML】聚类：Kmeans算法与DBSCAN算法

聚类是无监督学习问题，没有标签，难点在于模型评估及调参。

Kmeans聚类算法

  假设我们想要将数据聚类成$K$个组，K-means方法的工作流程为:

1. 首先选择$K$个随机的点，称为聚类中心（cluster centroids）或质心;
2. 对于数据集中的每一个数据，按照距离$K$个中心点的距离，将其与距离最近的中心点关联起来，与同一个中心点关联的所有点聚成一类；
3. 计算每一个组的平均值，将该组质心移动到平均值的位置；
4. 重复步骤，直至中心点不再变化。

Kmeans可视化

  K-means最小化问题，是要最小化所有的数据点与其所关联的聚类中心点之间的距离之和，因此 K-均值的代价函数（又称畸变函数 Distortion function）为：
$$J(c^{(1)},...,c^{(N)};{\mu }_1,...,{\mu }_k)=\frac{1}{N}\sum _{i=1}^N\Vert x^{(i)}-u^{c(i)}{\Vert }^2$$
其中，$N$为样本个数，${\mu }_{c^{(i)}}$表示与样本$x^{(i)}$最近的聚类中心点。

  K-means算法具有如下特点，

• 简单，快速，适合常规数据集，调参的参数仅为簇数$K$，可解释性比较强。
• 对离群点敏感。
• 无法保证收敛到全局最优值，常使用不同的初始值进行多次试验，对初始值敏感。
• K值是人为给定的，如果让机器自己去找类别的个数，有AP聚类算法。K值难以事先选取，交叉验证不大适合，所以常采用“拐点法”（肘部法则）。
• K-Means的一个重要的假设是：数据之间的相似度可以使用欧氏距离度量，如果不能使用欧氏距离度量，要先把数据转换到能用欧氏距离度量，这一点很重要（注：可以使用欧氏距离度量的意思就是欧氏距离越小，两个数据相似度越高）。由于采用欧氏距离，无法直接计算类别型变量。一般需要对数据先作标准化处理。
• 复杂度与样本呈线性关系。
• 很难发现任意形状的簇。
• 相对于高斯混合模型而言收敛速度快，因而常用于高斯混合模型的初始值选择。

从EM算法角度看K-Means

  K-means的目标是将样本集划分为K个簇，使得同一个簇内样本的距离尽可能小，不同簇之间的样本距离尽可能大，即最小化每个簇中样本与质心的距离。K-means属于原型聚类(prototype-based clustering)，原型聚类指聚类结构能通过一组原型刻画，而原型即为样本空间中具有代表性的点。在K-means中，这个原型就是每个簇的质心$\mu$。

  从EM算法的观点来看，K-means的参数就是每个簇的质心$\mu$，隐变量为每个样本的所属簇。如果事先已知每个样本属于哪个簇，则直接求平均即可得到$\mu$。但现实中不知道的情况下，则需要运用EM的思想：

  假设有$K$个簇，先随机选定$K$个点作为质心${\mu }_1,{\mu }_2,...,{\mu }_k$：

1. 固定${\mu }_k$，将样本划分到距离最近的${\mu }_k$所属的簇中。若用$r_{nk}$表示第n个样本所属的簇，则
   $$r_{nk}=\{\begin{array}{ll}1& \text{ if }k={\mathrm{argmin}}_j{\Vert {\mathbf{x}}_n-{\mathbf{\mu }}_j\Vert }^2\\ 0& \text{ otherwise }\end{array}$$
2. 固定$r_{nk}$，根据上一步的划分结果重新计算每个簇的质心。由于我们的目标是最小化每个簇中样本与质心的距离，可将目标函数表示为$J={\sum }_{n=1}^N{r}_{nk}\Vert x_n-{\mu }_k{\Vert }^2$，要最小化$J$则对${\mu }_k$求导得$2{\sum }_{n=1}^N{r}_{nk}(x_n-{\mu }_k)=0$，则
   $${\mu }_k=\frac{{\sum }_n{r}_{nk}{x}_n}{{\sum }_n{r}_{nk}}$$
   即簇中每个样本的均值向量。

  上面两步分别更新$r_{nk}$和${\mu }_k$就对应了EM算法中的E步和M步。和EM算法一样，K-means每一步都最小化目标函数$J$，因而可以保证收敛到局部最优值，但在非凸目标函数的情况下不能保证收敛到全局最优值。

应用：
图像压缩：将像素点聚类。

DBSCAN算法

基本概念

• $ϵ$邻域的距离阈值： $ϵ>0$，对象O的$ϵ$邻域是指，以O为中心，$ϵ$为半径的空间。
• 邻域密度阈值MinPts： 核心对象的$ϵ$邻域中包含的对象数量的最小值。
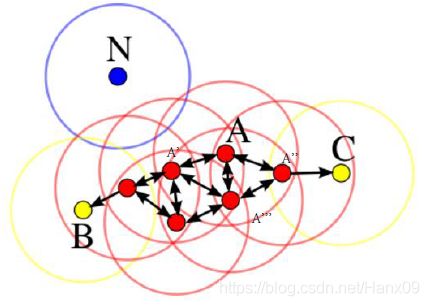
• 核心对象： 如果某个对象的$ϵ$邻域内的至少包含MinPts个对象，则该对象是核心对象。（A）
• 直接密度可达： 如果对象$p$在核心对象$q$的$ϵ$邻域内，则$p$是从$q$直接密度可达的。
• 密度可达： 若存在对象序列$q_0,q_1,...,q_k$，对任意的$i$，$q_i$是从$q_{i-1}$直接密度可达的，则称从$q_0$到$q_k$密度可达。这实际上是直接密度可达的“传播”。
• 密度相连： 若存在对象$q$，使得$p_1$和$p_2$从$q$都是密度可达的，则称$p_1$和$p_2$是密度相连的。
• 边界点： 属于某一个类的非核心点，不能发展下线了，即不存在从该点直接密度可达的点。（B、C）
• 噪声点： 不属于任何一个类簇的点，从任何一个核心点出发都是密度不可达的。（N）

工作流程

输入：数据集$D$，半径$ϵ$，密度阈值$MinPts$。

参数选择

k-距离：
  给定数据集$P=p(i);i=0,1,\dots n$，对于任意点$P(i)$，计算点$P(i)$到集合$P$的子集$S=p(1),p(2),\dots ,p(i-1),p(i+1),\dots ,p(n)$中所有点之间的距离，距离按照从小到大的顺序排序，假设排序后的距离集合为$D=d(1),d(2),\dots ,d(k-1),d(k),d(k+1),\dots ,d(n)$，则$d(k)$就被称为k-距离。也就是说，k-距离是点$p(i)$到所有点（除了$p(i)$点）之间距离第k近的距离。对待聚类集合中每个点$p(i)$都计算k-距离，最后得到所有点的k-距离集合$E=e(1),e(2),\dots ,e(n)$。

根据经验计算半径Eps：
  根据得到的所有点的k-距离集合$E$，对集合$E$进行升序排序后得到k-距离集合$E’$，需要拟合一条排序后的$E’$集合中k-距离的变化曲线图，然后绘出曲线，通过观察，将急剧发生变化的位置所对应的k-距离的值，确定为半径Eps的值。

根据经验计算最少点的数量MinPts：
  确定MinPts的大小，实际上也是确定k-距离中k的值，一般取得小一些，多次尝试。

优势与劣势

优势：

• 不需要指定簇个数
• 擅长找到离群点（检测任务）
• 可以发现任意形状的簇
• 指定两个参数就够了

劣势：

• 高维数据有些困难（可以做降维）
• Sklearn中效率很慢（数据削减策略）
• 参数难以选择（参数对结果的影响非常大）

DBSCAN可视化

评估聚类模型

轮廓系数

$$s(i)=\frac{b(i)-a(i)}{\max \{a(i),b(i)\}}$$
$$s(i)=\{\begin{array}{l}1-\frac{a(i)}{b(i)},a(i)<b(i)\\ 0,a(i)=b(i)\\ \frac{a(i)}{b(i)}-1,a(i)>b(i)\end{array}$$

• 计算样本$i$到同簇其他样本的平均距离$a(i)$。$a(i)$越小，说明样本i越应该被聚类到该簇。将$a(i)$称为样本i的簇内不相似度。
• 计算样本$i$到其他某簇Cj 的所有样本的平均距离$bij$，称为样本$i$与簇Cj 的不相似度。定义为样本i的簇间不相似度：$b(i)=minbi1,bi2,...,bik$

• $s(i)$接近1，则说明样本$i$聚类合理
• $s(i)$接近-1，则说明样本$i$更应该分类到另外的簇
• 若$s(i)$近似为0，则说明样本$i$在两个簇的边界上。

>>> from sklearn import metrics 
>>> scores = []
>>> for k in range(2,20):
>>>    labels = KMeans(n_clusters=k).fit(X).labels_
>>>    score = metrics.silhouette_score(X, labels)
>>>    scores.append(score)

>>> scores#不同k的轮廓系数
[0.6917656034079486,
 0.6731775046455796,
 0.5267665961530135,
 0.422548733517202,
 0.4559182167013377,
 0.43776116697963124,
 0.38946337473125997,
 0.39746405172426014,
 0.3915697409245163,
 0.32472080133848924,
 0.3459775237127248,
 0.31221439248428434,
 0.30707782144770296,
 0.31834561839139497,
 0.2849514001174898,
 0.23498077333071996,
 0.1588091017496281,
 0.08423051380151177]

————————————————
参考：
DBSCAN聚类原理