岭回归详解 从零开始 从理论到实践

一、岭回归的理解

1.1、LinearRegression的回顾

在标准线性回归中，通过最小化真实值($y_i$)和预测值(${\hat{y}}_i$)的平方误差来训练模型，这个平方误差值也被称为残差平方和(RSS, Residual Sum Of Squares):
$$RSS=\sum _{i=1}^n(y_i-{\hat{y}}_i{)}^2$$
最小二乘法即最小化残差平方和，为：
$$J_{\beta }(\beta )=\underset{\beta }{\mathrm{argmin}}\sum _{i=1}^p(y_i-x_i{\beta }_i-{\beta }_0{)}^2$$

将其化为矩阵形式：
$$\begin{array}{r}{J}_{\beta }(\beta )=\underset{\beta }{\mathrm{argmin}}(y-X\beta {)}^T(y-X\beta )\end{array}$$
求解为：
$$\beta =(X^{T}X)X^{T}y$$
由于求解 $\beta$，需要假设 $X^{T}X$ 为满秩矩阵。

然而现实任务中 $X^{T}X$ 往往不是满秩矩阵或者某些列之间的线性相关性比较大，例如存在许多任务中，会出现变量数(属性数)远超过样例数，导致 $X$ 的列数多于行数，$X^{T}X$ 显然不满秩，即 $X^{T}X$ 的行列式接近于0，即接近于奇异，此时计算是误差会很大，可解出多个 $\beta$(有用的方程组数少于未知数的个数时，没有唯一解，即有无穷多个解)，它们都能使均方误差最小化。即在多元回归中，特征之间会出现多重共线问题，使用最小二乘法估计系数会出现系数不稳定问题，缺乏稳定性和可靠性。

参考1 n阶行列式
参考2 岭回归

1.2、岭回归 - Ridge Regression

为了解决上述问题，我们需要将不适定问题转化为适定问题，在矩阵 $X^{T}X$ 的对角线元素上加入一个小的常数值 $\lambda$，然后取其逆求得系数：
$${\hat{\beta }}_{ridge}=(X^{T}X+\lambda I_n{)}^{-1}{X}^{T}Y$$

• $I_n$ 是单位矩阵，对角线全是1，类似与“山岭
• $\lambda$ 是岭系数，改变其数值可以改变单位矩阵对角线的值

随后，代价函数 $J_{\beta }(\beta )$ 在 $RSS$ 的基础上加入了对系数值的惩罚，变为：
$$\begin{array}{rl}{J}_{\beta }(\beta )& =RSS+\lambda \sum _{j=0}^n{\beta }_j^2\\ & =RSS+\lambda ||\beta |{|}^2\end{array}$$
矩阵形式为：
$$\begin{array}{rl}{J}_{\beta }(\beta )& =\sum _{i=1}^p(y_i-X_i\beta {)}^2+\lambda \sum _{j=0}^n{\beta }_j^2\\ & =\sum _{i=1}^p(y_i-X_i\beta )+\lambda ||\beta |{|}^2\end{array}$$

• ${\beta }_j$是总计$p$个特征中第$j$个特征的系数
• $\lambda$是超参数，用来控制对 ${\beta }_j$的惩罚强度，$\lambda$值越大，生成的模型就越简单。$\lambda$的理想值应该是像其他超参数一样通过调试获得的。在sklearn中，使用alpha参数来设置 $\lambda$。
• $||\beta |{|}^2$ 为$L2$范数
• $\lambda ||\beta |{|}^2$ 为收缩惩罚项(shrinkage penalty)，因为它试图“缩小”模型，减小线性回归模型的方差。它也称为正则化的 $L2$范数。

岭回归在估计系数 $\beta$ 时，设置了一个特定形式的约束，使得最终得到的系数的 $L2$ 范数较小。

假设得到两个回归模型：
$h_1=x_1+x_2+x_3+x_4$
$h_2=0.4x_1+4x_2+x_3+x_4$
两个模型得到的残差平方和相同，但是
$h_1$的惩罚项为$4\lambda$，$h_2$的惩罚项为$18.16\lambda$
相比得出，岭回归更倾向于 $h1$

岭回归的特点：
岭回归是一种改良的最小二乘估计法，通过放弃最小二乘法的无偏性，以损失部分信息、降低精度为代价获得回归系数，它是更为符合实际、更可靠的回归方法，对存在离群点的数据的拟合要强于最小二乘法。

不同与线性回归的无偏估计，岭回归的优势在于它的无偏估计，更趋向于将部分系数向0收缩。因此，它可以缓解多重共线问题，以及过拟合问题。但是由于岭回归中并没有将系数收缩到0，而是使得系数整体变小，因此，某些时候模型的解释性会大大降低，也无法从根本上解决多重共线问题。

二、sklearn的使用

2.1、方法、参数与属性

2.1.1、特征标准化 - StandardScaler

学习算法的目标函数中使用的许多元素（例如支持向量机的RBF内核或线性模型的L1和L2正则化器）都假定所有特征都围绕0居中并且具有相同顺序的方差。

如果某个特征的方差比其他特征大几个数量级，则它可能会支配目标函数，并使估计器无法按预期从其他特征中正确学习。

class sklearn.preprocessing.StandardScaler(*, copy=True, with_mean=True, with_std=True)

模型类方法：

函数	说明	输入	返回
StandardScaler.fit_transform(X)	拟合数据，并转换它。转化成均值为0，方差为1分布的数组	数组X	数组

参考3 标准化官网
参考4

2.1.2、岭回归 - Ridge

带有 $L2$ 正则化的最小二乘法

class sklearn.linear_model.Ridge(alpha=1.0, *, fit_intercept=True, normalize=False, copy_X=True, max_iter=None, tol=0.001, solver='auto', random_state=None)

模型对象的参数：

参数	取值	说明
alpha	float, default=1.0	正则强度，必须是一个正浮点数。正则化改善了问题的条件，并减少了估计的方差。较大的值表示更强的正则化
fit_intercept	bool, default=True	是否拟合该模型的截距。如果设置为false，则在计算中将不使用截距
normalize	bool, default=False	归一化。fit_intercept设置为False时，将忽略此参数。如果为True，则将在回归之前通过减去均值并除以l2-范数来对回归变量X进行归一化。
copy_X	bool, default=True	如果为True，将复制X；否则为X自身。
max_iter	int, default=None	共轭梯度求解器的最大迭代次数。
tol	float, default=1e-3	结果的精度
solver	{‘auto’, ‘svd’, ‘cholesky’, ‘lsqr’, ‘sparse_cg’, ‘sag’, ‘saga’}, default=‘auto’	用于计算例程的求解器
random_state	int, default=None	随机种子

模型类的方法：
将模型类通过样本数据转化成模型实例，即拟合模型。

参数	取值	说明	输出
Ridge.fit(X, y)	X表示自变量X，即属性值，类似数组或稀疏矩阵；y表示因变量，即结果标签，类似数组	通过X和y，拟合Ridge模型	模型实例 model

模型实例的方法：

参数	取值	说明	输出
model.get_params()	bool，default=True	获取此估计器的参数	各参数以字典形式
model.set_params(param=XXX)	括号内指定param=XXX	设置此估计器的参数	无
model.predict(X)	类似数组或稀疏矩阵	使用线性模型进行预测	预测值 predictions，类似数组

模型实例的属性：

参数	说明
model.coef_	回归系数，权重向量
model.n_iter	每个目标的实际迭代次数。仅适用于sag和lsqr求解器。其他求解器将返回None。
model.intercept_	线性模型的截距，fit_intercept = False时，值为0.0

预测结果的评估方法：

参数	取值	说明	输出
predictions.score(X, y)	X为新的数据集，y为新数据集的预测结果	模型的评估	R^2决定系数预测

参考5 岭回归官网

2.1.3、内置交叉验证岭回归 - RidgeCV

在岭回归的基础上，内置了交叉验证。默认情况下，它执行有效的“留一法”交叉验证。

RidgeCV不同于Ridge可以输入多个超参数Alpha，以方便得出最佳Alpha。

class sklearn.linear_model.RidgeCV(alphas=0.1, 1.0, 10.0, *, fit_intercept=True, normalize=False, scoring=None, cv=None, gcv_mode=None, store_cv_values=False, alpha_per_target=False)

模型对象的参数：

参数	取值	说明
alphas	float, default=(0.1, 1.0, 10.0)	要尝试的Alpha值数组。同样表示正则强度，值必须是一个正浮点数。正则化改善了问题的条件，并减少了估计的方差。较大的值表示更强的正则化
fit_intercept	bool, default=True	是否拟合该模型的截距。如果设置为false，则在计算中将不使用截距
normalize	bool, default=False	归一化。fit_intercept设置为False时，将忽略此参数。如果为True，则将在回归之前通过减去均值并除以l2-范数来对回归变量X进行归一化。
scoring	string, callable, default=None	带有scorer(estimator, X, y)签名的字符串或计分器可调用对象/函数 。如果为None，则当cv为’auto’或为None时（即，使用留一法交叉验证时）为负均方误差，否则为r2得分。
cv	int，default，交叉验证生成器或迭代器	确定交叉验证拆分策略。
gcv_mode	{‘auto’, ‘svd’, ‘eigen’}, default=‘auto’	指示执行“留一法”交叉验证时要使用的策略的标志。
store_cv_values	bool, default=False	指示是否应将与每个alpha对应的交叉验证值存储在cv_values_属性中的标志。该标志仅与cv=None（即使用“留一法”交叉验证）兼容。
alpha_per_target	bool, default=False	指示是否alphas分别针对每个目标（对于多输出设置：多个预测目标）分别优化α值（从参数列表中选取）的标志 。设置True为时，拟合后，该alpha_属性将包含每个目标的值。设置False为时，所有目标均使用单个alpha。

模型类的方法：
将模型类通过样本数据转化成模型实例，即拟合模型。

参数	取值	说明	输出
RidgeCV.fit(X, y)	X表示自变量X，即属性值，类似数组或稀疏矩阵；y表示因变量，即结果标签，类似数组	通过X和y，拟合Ridge模型	模型实例 model

模型实例的方法：

参数	取值	说明	输出
model.get_params()	bool，default=True	获取此估计器的参数	各参数以字典形式
model.set_params(param=XXX)	括号内指定param=XXX	设置此估计器的参数	无
model.predict(X)	类似数组或稀疏矩阵	使用线性模型进行预测	预测值 predictions，类似数组

模型实例的属性：

参数	说明
model.coef_	回归系数，权重向量
model.intercept_	线性模型的截距，fit_intercept = False时，值为0.0
model.cv_values	每个Alpha的交叉验证值（仅当store_cv_values=True和时可用 cv=None）。之后fit()被调用，此属性将包含均方误差（默认）或值{loss,score}_func函数（如果在构造函数中提供）。
alpha_	估计器的正则参数，或者，如果alpha_per_target=True，每个目标的估计器正则参数
best_score_	alpha最优时估计器的得分，或者，如果alpha_per_target=True，每个目标的得分

预测结果的评估方法：

参数	取值	说明	输出
predictions.score(X, y)	X为新的数据集，y为新数据集的预测结果	模型的评估	R^2决定系数预测

参考6 交叉验证岭回归官网
参考7
参考8

2.2、实例应用

2.2、简单案例

同样以波士顿房价数据为例：

from sklearn.linear_model import Ridge
from sklearn.preprocessing import StandardScaler
from sklearn.datasets import load_boston

# 加载数据
boston = load_boston()
features = boston.data
target = boston.target

# 特征标准化
scaler = StandardScaler()
features_standardized = scaler.fit_transform(features)

# 创建线性回归对象
ridge = Ridge(alpha=0.5)
# 拟合模型
model = ridge.fit(features_standardized, target)

# 回归系数
model.coef_
"""
array([-0.92396151,  1.07393055,  0.12895159,  0.68346136, -2.0427575 ,
        2.67854971,  0.01627328, -3.09063352,  2.62636926, -2.04312573,
       -2.05646414,  0.8490591 , -3.73711409])
"""

2.3、多个超参数的设定 -RidgeCV

from sklearn.linear_model import RidgeCV
from sklearn.preprocessing import StandardScaler
from sklearn.datasets import load_boston

# 加载数据
boston = load_boston()
features = boston.data
target = boston.target

# 特征标准化
scaler = StandardScaler()
features_standardized = scaler.fit_transform(features)

# 创建线性回归对象
ridge_cv = RidgeCV(alphas=[0.1, 1.0, 10.0])
# 拟合模型
model = ridge_cv.fit(features_standardized, target)

model.score(features_standardized, target)
"""
0.7406304514762481
"""

model.best_score_
"""
-23.718112644972546
"""

# 查看最优模型的alpha值
model.alpha_
"""
1.0
"""

2.4、多项式回归+岭回归案例

改编多项式回归+线性回归案例，使用岭回归来测试不同degree的图像显示。

# 导入库
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import Ridge
from sklearn.preprocessing import PolynomialFeatures
from sklearn.pipeline import make_pipeline

# 生成训练集和测试集
def f(x):
    """ 使用多项式插值拟合的函数"""
    return x * np.sin(x)
# 为了画函数曲线生成的数据
x_plot = np.linspace(0, 10, 100)
# 生成训练集
x = np.linspace(0, 10, 100)
rng = np.random.RandomState(0)
rng.shuffle(x)
x = np.sort(x[:30])
y = f(x)
# 转换为矩阵形式
X = x[:, np.newaxis]
X_plot = x_plot[:, np.newaxis]

# 可视化
colors = ['teal', 'yellowgreen', 'gold']
linestyles=["-","--",":"]
# lw = 2
fig = plt.figure(figsize=(12,6))
plt.plot(x_plot, f(x_plot), color='cornflowerblue', linewidth=1,
         label="ground truth")
plt.scatter(x, y, color='navy', s=10, marker='o', label="training points")
for count, degree in enumerate([3, 4, 5]):
    model = make_pipeline(PolynomialFeatures(degree), Ridge())
    model.fit(X, y)
    y_plot = model.predict(X_plot)
    plt.plot(x_plot, y_plot, color=colors[count], linestyle=linestyles[count],linewidth=2,
             label="degree %d" % degree)
    plt.legend(loc='lower left')
plt.show()
# fig.savefig('./img/4.6.3-PolynomialRegression.png',dpi=600)

结果展示：

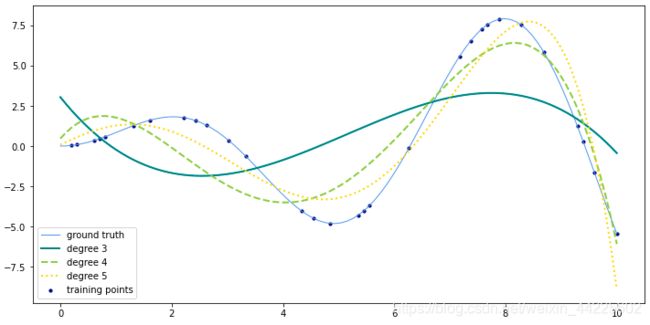
可见阶数越高，曲线的弯曲形状越大，越接近函数曲线。

---