万字文详解二叉树OJ面试题

✨hello，愿意点进来的小伙伴们，你们好呐！
✨ 系列专栏：【数据结构】
本篇内容：二叉树常见OJ题的讲解
作者简介:一名现大二的三非编程小白

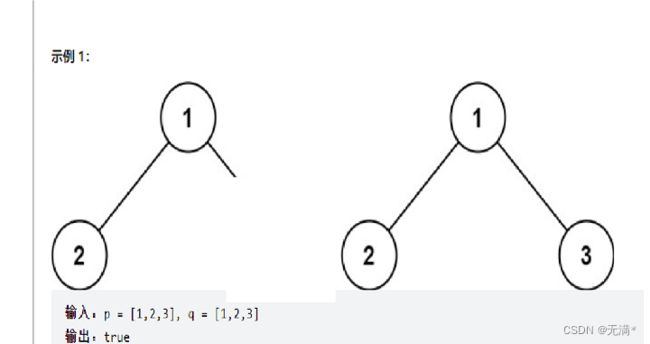
1. 相同的树

链接: https://leetcode.cn/problems/same-tree/

思路：
1. 先找出二叉树不同的条件：
一个为null，一个不为null

两个节点的数不同

2.二叉树相同的条件：
两个节点都为null，节点的元素相同

class Solution {
    public boolean isSameTree(TreeNode p, TreeNode q) {
        if(p ==null && q == null){
            return true;
        }
        if(p != null && q == null || p == null && q != null){
            return false;
        }
        if(p.val != q.val){
            return false;
        }
        return isSameTree(p.left,q.left) && isSameTree(p.right,q.right);
    }
}

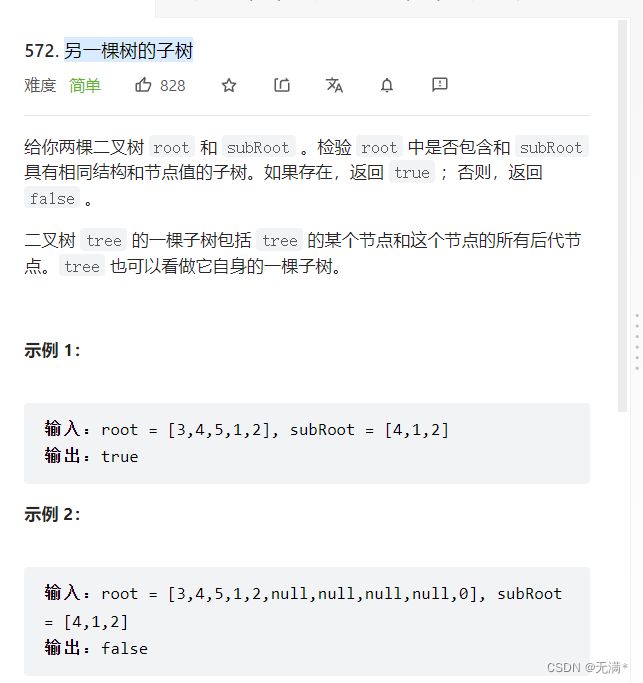
2.另一棵树的子树

链接: https://leetcode.cn/problems/subtree-of-another-tree/

思路：
1.先判断一棵树是否为null，若为null则返回 false
2.将一棵树与其要判断的子树比较判断是否为其子树，若不是就判断该树的左子树，再判断该树的右子树。最终都不是的情况下返回，false

class Solution {
    public boolean isSubtree(TreeNode root , TreeNode subRoot) {
        if(root == null ){
            return false;
        }
        if(isSameTree(root,subRoot)){
            return true;
        }
        if(isSubtree(root.left,subRoot)){
            return true;
        }
        if(isSubtree(root.right,subRoot)){
            return true;
        }
        return false;
    }

    public boolean isSameTree(TreeNode p, TreeNode q){
        if(p == null && q == null){
            return true;
        }
        if(p == null && q != null || p != null && q == null){
            return false;
        }
        if(p.val != q.val){
            return false;
        }

        return isSameTree(p.left,q.left) && isSameTree(p.right,q.right);
       
    }
}

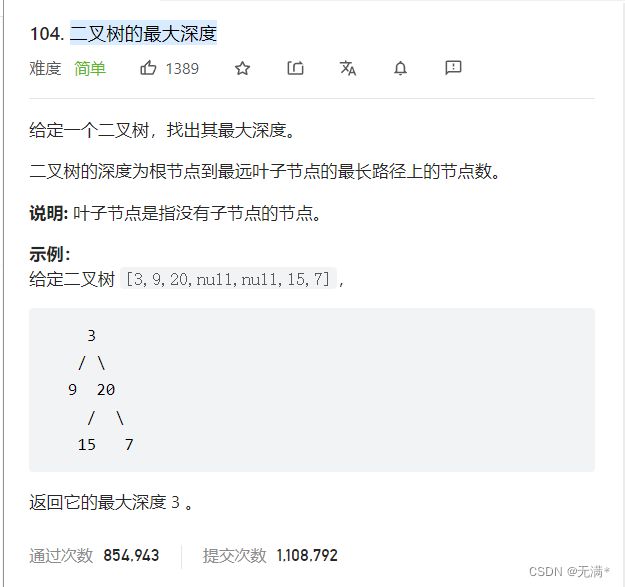
3.二叉树的最大深度

链接: https://leetcode.cn/problems/maximum-depth-of-binary-tree/

class Solution {
    public int maxDepth(TreeNode root) {
        if(root == null){
            return 0;
        }
        int leftHeight = maxDepth(root.left);
        int rightHeight = maxDepth(root.right);
        
        return leftHeight > rightHeight ? leftHeight + 1 : rightHeight + 1;
    }
}

4. 二叉树的层序遍历

链接: https://leetcode.cn/problems/binary-tree-level-order-traversal/

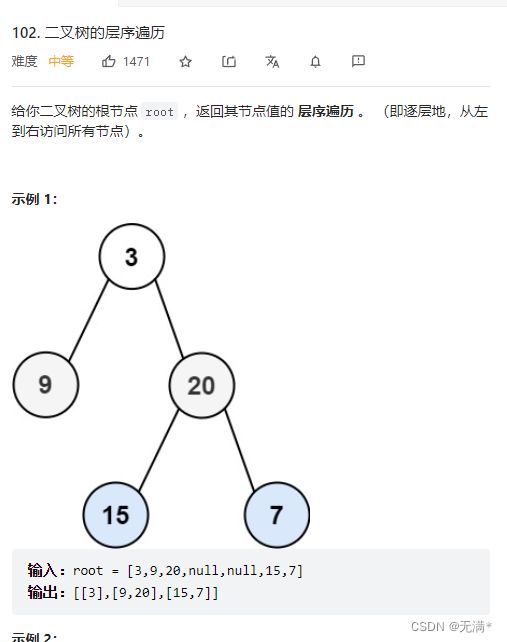
我们可以创建一个队列，用前序遍历当队列不为null时，将树中的节点放入队列中。定义变量size来计算当前队列中的大小
然后定义一个变量cur来存储从队列中弹出的节点，又将cur的左右子树节点存储进队列中，将弹出的节点存储到ArrayList中。

代码如下：

class Solution {
    public List<List<Integer>> levelOrder(TreeNode root) {
        List<List<Integer>> list = new ArrayList<>();
        //如何确定每一层数

        if(root == null){
            return list;
        }
        Queue<TreeNode> queue = new LinkedList();
        queue.offer(root);
        while(!queue.isEmpty()){
            int size = queue.size();
            List<Integer> tmp = new ArrayList();
            while(size > 0){
                TreeNode cur = queue.poll();
                tmp.add(cur.val);
                size--;
                if(cur.left != null){
                    queue.offer(cur.left);
                }
                if(cur.right != null){
                    queue.offer(cur.right);
                }
            }
            list.add(tmp);
        }
        return list;

    }
}

5. 判断一棵树是否完全二叉树

判断一颗树是否完全二叉树和层序遍历的思路基本一致。
区别是：不用判断二叉树的左右子树是否为null，全部都加入队列中。
若该树是完全二叉树，在最后的队列中的节点都为null

 //判断一颗树是否完全二叉树
    public boolean isCompleteTree(TreeNode root){
        if(root == null){
            return true;
        }
        Queue<TreeNode> queue = new LinkedList<>();
        queue.offer(root);
        while(!queue.isEmpty()){
            TreeNode cur = queue.poll();
            if(cur == null){
                break;
            }
            queue.offer(root.left);
            queue.offer(root.right);
        }
        while(!queue.isEmpty()){
            if(queue.poll() != null){
                return false;
            }
        }
        return true;
    }

6. 路径总和

链接: https://leetcode.cn/problems/path-sum/

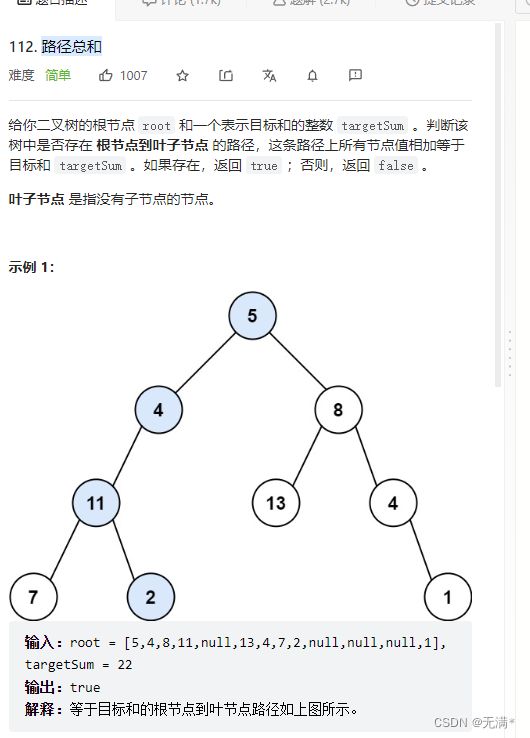
思路：
1. 空树情况下返回false；
2. 当一颗树的左子树右子树都为null，则该节点为叶子节点，所以来判断该节点的val值与目标值去进行比较，相等返回true，不等返回false。
3. 对左子树进行判断再对右子树进行判断，若都没有找到该路径困，则返回false

class Solution {
    public boolean hasPathSum(TreeNode root, int targetSum) {
        if(root == null){
            return  false;
        }
        if( root.right == null && root.left == null){
            if(root.val == targetSum){
                return true;   
            }else{
                return false;
            }
        }
        boolean ret1 = hasPathSum(root.left,targetSum - root.val);
        if(ret1 == true){
            return true;
        }
        boolean ret2 = hasPathSum(root.right,targetSum - root.val);
        if(ret2 == true){
            return true;
        }
        return false;
    }
}

7. 二叉树的最近公共祖先 （思路一）

链接: 二叉树的最近公共祖先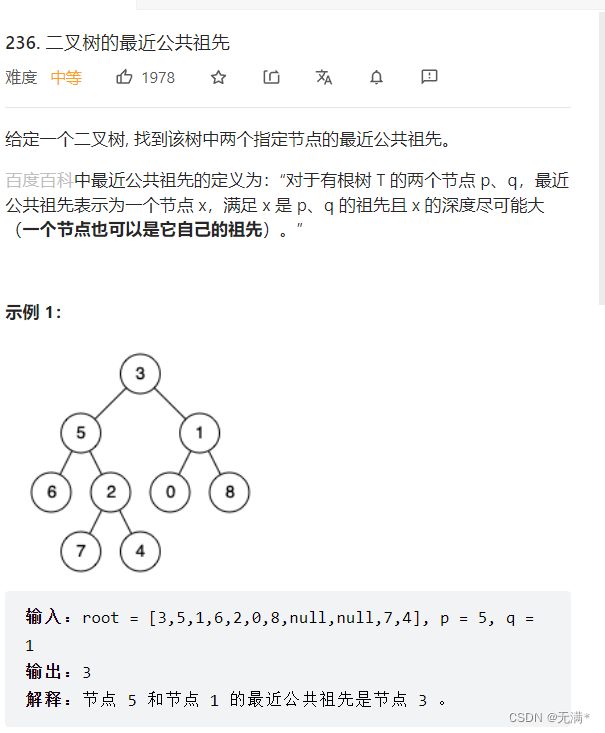
想要找到节点的公共祖先，我们可以很快的想到一种思路，要是可以知道一个节点的父节点就好了，我们可以通过父节点去比较，但是，在二叉树中，并没有父类节点一说，我们可以用什么方法来解决呢？

思路：
1. 我们可以将根节点到目标节点的路径存到一个栈中。
2. 然后将两个栈可能会大小不同，我们可以将空间较大的栈出栈，使两个栈空间大小相等。
3. 然后再让两个栈同时出栈，判断是否有相同的节点。

我们要怎么才能找到一个节点到根节点的路径呢？

创建一个栈，将节点从根节点开始，根 - 左 - 右，一个一个的入栈，如果遇到入栈的节点是我们要找的节点就返回true，如果遇到入栈的节点的左右节点都为null时，就将该节点出栈，返回false

public boolean findPath(TreeNode root,TreeNode target,Stack<TreeNode> stack){
        if(root == null || target == null){
            return false;
        }
        stack.push(root);
        if(root == target){
            return true;
        }
        boolean ret1 = findPath(root.left, target,stack);
        if(ret1 == true){
            return true;
        }

        boolean ret2 = findPath(root.right,target,stack);
        if(ret2 == true){
            return true;
        }
        stack.pop();
        return false;
    }

总代码如下：

class Solution {
    public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
        if(root == null || p == null || q == null){
            return null;
        }
        Stack<TreeNode> stack1 = new Stack();
        findPath(root,p,stack1);

        Stack<TreeNode> stack2 = new Stack();
        findPath(root,q,stack2);

        int size1 = stack1.size();
        int size2 = stack2.size();
        if(size1 > size2){
            int size = size1 - size2;
            while(size > 0){
                stack1.pop();
                size--;
            }
        }else{
            int size = size2 - size1;
            while(size > 0){
                stack2.pop();
                size--;
            }
        }

        while(stack1.peek() != stack2.peek()){
            stack1.pop();
            stack2.pop();
        }
        return stack1.peek();
    }
    public boolean findPath(TreeNode root,TreeNode target,Stack<TreeNode> stack){
        if(root == null || target == null){
            return false;
        }
        stack.push(root);
        if(root == target){
            return true;
        }
        boolean ret1 = findPath(root.left, target,stack);
        if(ret1 == true){
            return true;
        }

        boolean ret2 = findPath(root.right,target,stack);
        if(ret2 == true){
            return true;
        }
        stack.pop();
        return false;
    }
}

8. 二叉树的最近公共祖先 （思路二）

上面一种思路虽然最后可以将题目解出来，但是空间复杂度和时间复杂度都太高了，运行效率极低，现在我们来换另一种思路。
一颗树上两个节点要是有公共节点可以分为以下几种情况：
1.一个节点为另一个节点的祖先

2.两个节点分别在根节点的左右两侧

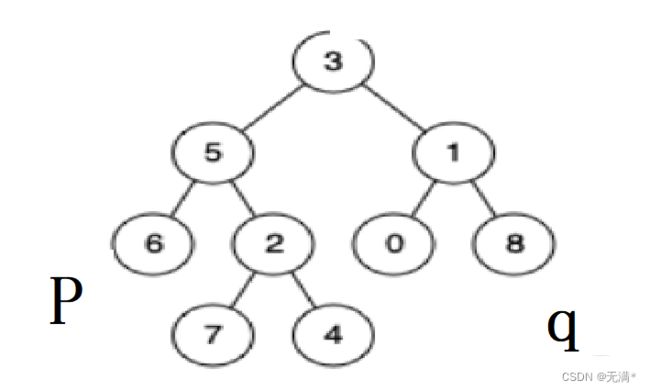
我们可以先判断根节点是否为两个节点其中之一，若不是，再去左子树寻找，再去右子树寻找。
最终判断，若一个根节点左右子树都找到了节点，那么就是第二种情况，返回该根节点。
若左子树找到了该节点，右子树为null，那么就返回左子树的节点，为第一种情况，
以此类推右子树找到该节点也类似。
最后若左右子树都没有找到该节点的话，就返回null。

class Solution {
    public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
        if(root == null){
            return null;
        }
        if(root == p || root == q){
            return root;
        }
        TreeNode leftNode = lowestCommonAncestor(root.left,p,q);
        TreeNode rightNode = lowestCommonAncestor(root.right,p,q);
        if(leftNode != null && rightNode != null){
            return root;
        }else if(leftNode != null && rightNode == null){
            return leftNode;
        }else if(rightNode != null && leftNode == null){
            return rightNode;
        }else{
            return null;
        }
    }
}

9. 二叉搜索树转双向链表

链接: 二叉搜索树转双向链表

二叉树就是通过链式来实现的，二叉树当中有left right 指向，那我们要如何将该指向转化成双向链表的相互指向呢？
**要将二叉搜索树转成排序后的双向链表，我们首先可以想到是用中序遍历的思想来实现有序的。 **
想要实现链表就要有前驱和后继，我们可以定义一个prev来存储节点。改变中序遍历得到的节点的指向来将二叉树转换成链表。
得到链表后，我们使用while循环就可以轻而易举的找到链表的头节点，从而返回。

public class Solution {
    public TreeNode Convert(TreeNode pRootOfTree) {
        if(pRootOfTree == null){
            return null;
        }
        convertChild(pRootOfTree);
        TreeNode head = pRootOfTree;
        while(head.left != null){
            head = head.left;
        }
        return head;
    }
    TreeNode prev = null;
    public void convertChild(TreeNode pCur){
        if(pCur == null){
            return;
        }
        convertChild(pCur.left);
        pCur.left = prev;
        if(prev != null){
            prev.right = pCur;
        }
        prev = pCur;
        convertChild(pCur.right);
    }
}

好啦，二叉树的oj题就先讲解到这里，期待大佬们的指点！！！