基于径向基函数RBF网络的手写数字分类(Matlab代码实现)
欢迎来到本博客❤️❤️❤️
博主优势:博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。
⛳️座右铭:行百里者,半于九十。、
目录
1 概述
2 运行结果
3 Matlab代码实现
1 概述
本文的目标是使用径向基函数网络对MNIST数据集中的手写数字(从0到9)进行分类。径向基函数网络是一种使用径向基函数(RBF)作为激活函数的人工神经网络。它有三层:
·输入图层
·具有RBF 激活功能的隐藏层·线性输出层
网络的输出是输入和神经元参数的径向基函数的线性组合。
下图说明了此结构:
每个隐藏单元由中心和展开/宽度定义。每个中心都是从训练集中抽取的样本。隐藏单元的激活由输入向量x与隐藏单元中心之间的距离决定。它们离得越近,隐藏单元的激活度就越高。它将径向基函数行为解释为激活函数。
学习过程包括两个阶段:
1.参数化隐藏单元:定义它们的中心和宽度。它可以通过随机选择或聚类来完成。这些中心直接取自训练数据集。2.通过计算插值矩阵查找隐藏单位和输出单位之间的权重值。
2 运行结果
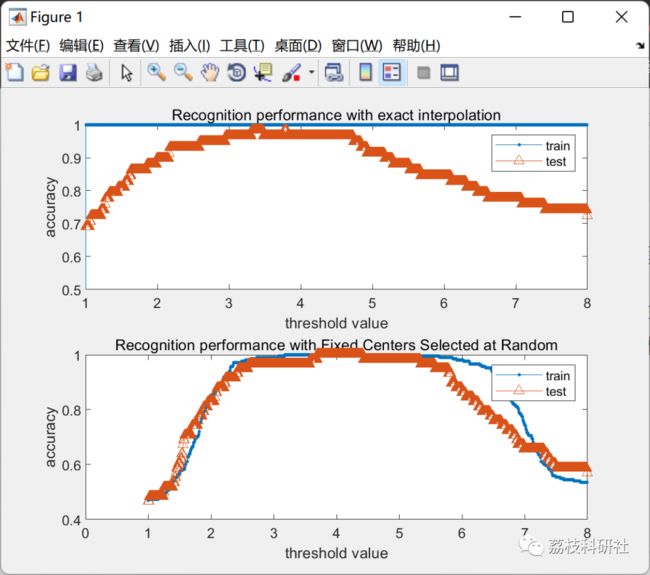
RBFN仅用于对手写数字1和8进行分类(通过提取1和8以外的标签样本来分类MNIST数据集)。对于每个样本,网络给出一个实际输出,并使用阈值将预测作为标签1和预测作为标签
8。预测产生的错误率/准确性取决于阈值。
已经测试了两种不同类型的隐藏单位(学习过程的第1阶段)︰
精确插值:我们定义与训练样本一样多的隐藏单元,每个隐藏单元的中心是一个训练样本·“随机选择固定中心"方法:随机选择M个训练样本来定义隐藏单元的中心
结果如下:
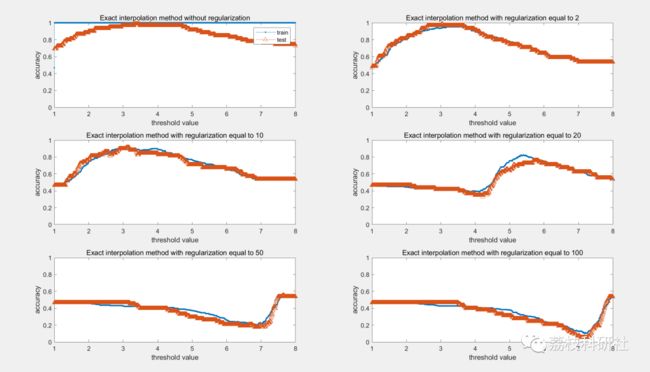
2.2 rbfn_regularization
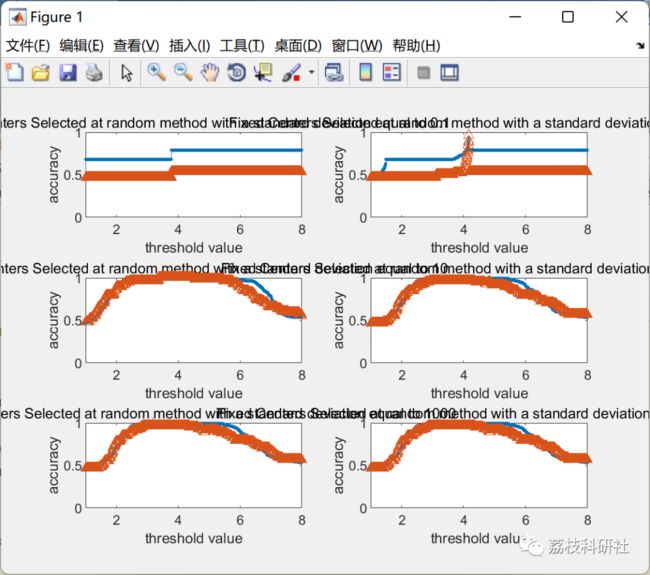
2.3 rbfn_tuning_std
我们可以注意到,无论使用精确插值方法的阈值如何,训练集的识别性能均为1。事实上,RBFN的输出和训练样本的标签之间存在精确的拟合。关于“随机选择的固定中心"方法,训练集的准确性不如精确插值的训练集那么完美。事实上,由于隐藏单元的数量较少,因此不再有确切的拟合。它为测试集带来更好的结果。
简而言之,RBEN可能方便拟合给定数据集(训练集的精度非常高),但可能会过度拟合!必须选择正确数量的隐藏单元(不要太高)并使用正则化。
部分代码:
% Compute the weights based on the interpolation matrix found with the
% Fixed Centers Selected at random method
phi_std_train = interpolation_matrix(train_data, M, mu_random, sigma, true);
weights_std_matrix(:,i) = inv(phi_std_train' * phi_std_train) * (phi_std_train' * train_classlabel');
y_train_std = phi_std_train * weights_std_matrix(:,i);
% Output of the test set
phi_std_test = interpolation_matrix(test_data, M, mu_random, sigma, true);
y_test_std = phi_std_test * weights_std_matrix(:,i);
% Evaluation of the recognition performance
[thres_std, train_accuracy_std, test_accuracy_std] = recognition_performance(y_train_std, train_classlabel_logical, y_test_std, test_classlabel_logical, 1000);
% Plot the result
subplot(length(std)/2, 2, i)
plot(thres_exact, train_accuracy_std,'.-',thres_exact, test_accuracy_std,'^-');
axis([1,8,0,1]);
xlabel('threshold value')
ylabel('accuracy')
title(['Fixed Centers Selected at random method with a standard deviation equal to ' num2str(std(i))])
end