深度学习笔记（52） 知识蒸馏

---

1. 简介

化学提及到蒸馏：加热液体汽化，再使蒸气液化，从而除去其中的杂质，获得所需要的产品

知识蒸馏也比较相似
利用一个大模型（教师模型）萃取知识，将其提取（迁移）到一个小模型（学生模型）上

通过上述的压缩已训练好的大模型方式，知识蒸馏就可以轻量化神经网络，得到小模型
然后就可以部署在边缘计算设备，实现算法应用落地

压缩已训练好的大模型方式：

• 知识蒸馏
• 权值量化：权重数据类型 float32 -> int8
• 剪枝：权重剪枝：对权重数值按照大小排序，把排后面的一定比例的值设为0使其失效；滤波器剪枝：对卷积核组进行纵向的修剪；通道剪枝：对卷积核组进行横向的修剪；层剪枝：直接删除整个卷积层

---

2. 知识的表示与迁移

在训练一个虎的识别时，通过hard targets的标签进行训练，之后将图片出入模型进行识别后得到一个soft targets
从soft targets中可以看出虎的概率是比较大的，识别为猫和车的概率都是比较小的
同样可以看出不同类别的相关性，如虎和猫存在一定相似性，而和车关联就比较少了
因此soft targets包含了更多的信息，如非正确类别概率的相对大小

那么可以用hard targets的标签训练教师模型输出soft targets，再将soft targets作为标签训练学生模型

---

3. 蒸馏温度T

如果对soft Target的输出信息还不满意，可以新增一个 蒸馏温度T
蒸馏温度T使用在softmax函数中，修正输出标签

$softmax(Z_i)=\frac{e^{Z_i}}{{\sum }_1^C{e}^{Z_c}}$ > > > $q=\frac{e^{Z_i/T}}{{\sum }_1^C{e}^{Z_c/T}}$

softmax是做归一化，凸显每个分类之间的差别，且和为1
C：类别数量；i：当前类别编号
具体可以参考《深度学习笔记（51） 基础知识》

当T=1时，还是原始的softmax函数
当T=3时，可以看相关分类的相似度降低了，其他不相关分类的相似度有所增加

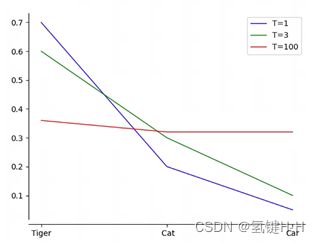
当T变大，每个分类所获得的相似度就越平均，越小会发现类别的相似度会很大

---

4. 知识蒸馏过程

1. 选用一个已经训练完成的教师模型，然后输入训练集数据，进行数据推算且调整蒸馏温度T=t 的softmax，得到 soft labels
2. 再把训练集数据输入训练学生模型，进行数据推算，进行数据推算且调整蒸馏温度T=t 的softmax，得到 soft predictions，然后和教师模型的 soft labels 进行相似度比较求 蒸馏损失 distillation loss
3. 学生模型进行数据推算时还输出蒸馏温度T=1 的原softmax，得到 hard predictions，与训练集数据标签 hard labels 进行相似度比较求 学生损失 student loss
4. 按系数 $\alpha$ 和 $\beta$ 对 学生损失 student loss 和 蒸馏损失 distillation loss 进行求和得到 总损失 total loss

这样学生模型既考虑了标准标签，也考虑了教师模型的结果

---

4.1. student loss

学生损失 student loss 比较简单
上述提到，就是学生模型输出 hard predictions 和 数据标签 hard labels 进行使用 交叉熵 相似度损失
其他类别标签均为0，目标类别为1，则有 $studentloss=-log（x_i）=-log(softmax(Z_i))=-log(\frac{e^{Z_i}}{{\sum }_1^C{e}^{Z_c}})$

---

4.2. distillation loss

与学生损失 student loss 的区别就是其他类型的标签概率不再为0，且蒸馏温度T存在变化
需要每个类别一对一的求损失，再求和

$distillationloss=-\frac{1}{N}{\sum }_{j=1}^N{\sum }_{i=1}^C{y}_{ij}\ast log(x_{ij})$

N：训练集样本数量； $j$：当前样本编号；
C：类别数量； $i$：当前类别编号；
$x$：学生模型概率结果soft predictions； $y$：教师模型概率结果soft labels；

以上面提及到的 虎/猫/车 分类为例，
假设 教师模型 蒸馏温度T=t 的softmax 结果为：0.86 / 0.12 / 0.02
假设 学生模型 蒸馏温度T=t 的softmax 结果为：0.66 / 0.22 / 0.12

那么 蒸馏损失 $=-[0.86\ast log(0.66)+0.12\ast log(0.22)+0.02\ast log(0.12)]$

---

也可以参考下图，$i$ 代表当前样本编号

---

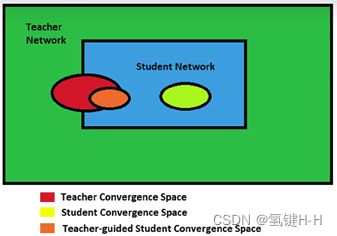
5. 背后的机理

读万卷书不如行万里路，行万里路不如阅人无数，阅人无数不如 名师指路

绿色是教师模型求解空间（比较大），蓝色是学生模型求解空间（比较小）
红色为教师模型的答案空间，浅绿色为学生模型的答案空间
橙色是在知识蒸馏的情况下得到的答案空间也是最优解

如果不加引导学生模型会在自己的求解空间中试探着寻找，最后找到浅绿色的答案
在增加了教师模型之后，学生模型查找求解空间时，教师模型会给予指导
让学生模型得到的答案更准确，或者让其往教师模型的答案空间靠

所以知识蒸馏会得到更轻便且效果好的模型

---

6. 应用场景

• 模型压缩
• 优化训练、防止过拟合（潜在的正则化）
• 无限大、无监督数据集的数据挖掘
• 少样本、零样本学习

知识蒸馏可以看成是迁移学习的一个特例
二者的相同点都是想从大数据、大模型学习知识到目标数据上，以提高模型在目标数据上的表现

不同的是，迁移学习是一个宏大的概念
而知识蒸馏就单纯指的是通过最小化教师模型与学生模型的不同
以达到较小的学生模型可以模拟逼近教师模型的作用
因此，知识蒸馏是实现迁移学习的一种有效形式

---

7. 代码实现

import torch
import torch.nn.functional as F
import torchvision
from torch import nn
from torchvision import transforms
from torch.utils.data import DataLoader


class StudentModel(nn.Module):
    def __init__(self, in_channels=1, num_classes=10):
        super(StudentModel, self).__init__()
        self.conv1 = nn.Conv2d(in_channels=in_channels, out_channels=1, kernel_size=7, stride=7)
        self.fc1 = nn.Linear(1 * 4 * 4, num_classes)

    def forward(self, x):
        x = F.relu(self.conv1(x))
        x = x.reshape(x.shape[0], -1)
        x = self.fc1(x)
        return x


class TeacherModel(nn.Module):
    def __init__(self, in_channels=1, num_classes=10):
        super(TeacherModel, self).__init__()
        self.out_channel_layer1 = 64
        self.out_channel_layer2 = 128
        self.conv1 = nn.Conv2d(in_channels=in_channels, out_channels=self.out_channel_layer1, kernel_size=3, stride=1, padding=1)
        self.conv2 = nn.Conv2d(in_channels=self.out_channel_layer1, out_channels=self.out_channel_layer2, kernel_size=3, stride=1, padding=1)
        self.fc1 = nn.Linear(self.out_channel_layer2 * 7 * 7, 1024)
        self.fc2 = nn.Linear(1024, num_classes)

    def forward(self, x):
        x = F.relu(self.conv1(x))
        x = F.max_pool2d(x, 2)
        x = F.relu(self.conv2(x))
        x = F.max_pool2d(x, 2)
        x = x.reshape(x.shape[0], -1)
        x = self.fc1(x)
        x = F.dropout(x, p=0.5)
        x = self.fc2(x)
        return x


def print_train(step_now, train_loader_len, epoch_now, epochs, lose_item):
    step_schedule_num = int(40 * step_now / train_loader_len)
    print("\r", end="")
    print("Train epoch: {}/{}\t step: {}/{} [{}{}] - loss: {:.5f}".format(epoch_now, epochs,
                                                                          step_now, train_loader_len,
                                                                          ">" * step_schedule_num,
                                                                          "-" * (40 - step_schedule_num),
                                                                          lose_item), end="")


def print_test(epoch_now, epochs, acc):
    print(("Test  epoch: {}/{}\t Accuracy:{:.4f}").format(epoch_now, epochs, acc))

device = torch.device("cuda" if torch.cuda.is_available() else "cpu")

# 1.载入训练集和测试集
train_dataset = torchvision.datasets.MNIST(root="dataset/", train=True, transform=transforms.ToTensor(), download=True)
test_dataset = torchvision.datasets.MNIST(root="dataset/", train=False, transform=transforms.ToTensor(), download=True)

train_loader = DataLoader(dataset=train_dataset, batch_size=32, shuffle=True)
test_loader = DataLoader(dataset=test_dataset, batch_size=32, shuffle=False)

train_loader_len = len(train_loader)
train_loader_dataset_len = len(train_loader.dataset)

# 2.设置教师模型训练
print("Teacher model train.")
model = TeacherModel().to(device)
loss_function = nn.CrossEntropyLoss()
Learning_Rate = 1e-4
optimizer = torch.optim.Adam(model.parameters(), lr=Learning_Rate)

epochs = 5  # 训练5轮
for epoch in range(epochs):
    model.train()
    step_now, losses = 0, []
    for data, targets in train_loader:
        data, targets = data.to(device), targets.to(device)
        # 优化器梯度初始化为零
        optimizer.zero_grad()
        # 前向预测
        preds = model(data)
        # 计算损失函数
        loss = loss_function(preds, targets)
        # 反向传播，优化权重
        loss.backward()
        # 结束一次前传+反传之后，更新优化器参数
        optimizer.step()
        # 显示进度
        step_now += 1
        losses.append(loss.item())
        print_train(step_now, train_loader_len, epoch+1, epochs, sum(losses)/len(losses))
    print()

    # 测试集上评估性能
    model.eval()
    num_correct = 0
    num_samples = 0
    with torch.no_grad():
        for x, y in test_loader:
            x, y = x.to(device), y.to(device)
            preds = model(x)
            predictions = preds.max(1).indices
            num_correct += (predictions == y).sum()
            num_samples += predictions.size(0)
        acc = (num_correct / num_samples).item()
    print_test(epoch+1, epochs, acc)

# 训练完成保存教师模型
teacher_model = model

# 3.设置普通小模型训练
print("Mini model train.")
model = StudentModel().to(device)
criterion = nn.CrossEntropyLoss()
optimizer = torch.optim.Adam(model.parameters(), lr=Learning_Rate)

epochs = 5
for epoch in range(epochs):
    model.train()
    for data, targets in train_loader:
        data, targets = data.to(device), targets.to(device)
        optimizer.zero_grad()
        preds = model(data)
        loss = criterion(preds, targets)
        loss.backward()
        optimizer.step()

    model.eval()
    num_correct = 0
    num_samples = 0
    with torch.no_grad():
        for x, y in test_loader:
            x, y = x.to(device), y.to(device)
            preds = model(x)
            predictions = preds.max(1).indices
            num_correct += (predictions == y).sum()
            num_samples += predictions.size(0)
            acc = (num_correct / num_samples).item()
    print_test(epoch+1, epochs, acc)


# 4.设置学生模型训练
print("Student model train.")
model = StudentModel().to(device)
temp = 5  # 蒸馏温度
hard_loss_alpha = 0.3  # hard_loss权重
hard_loss = nn.CrossEntropyLoss()
soft_loss = nn.KLDivLoss(reduction="batchmean")
optimizer = torch.optim.Adam(model.parameters(), lr=Learning_Rate)

epochs = 5
for epoch in range(epochs):
    model.train()
    for data, targets in train_loader:
        data, targets = data.to(device), targets.to(device)
        optimizer.zero_grad()

        # 学生模型预测
        student_preds = model(data)
        student_loss = hard_loss(student_preds, targets)

        # 教师模型预测
        teacher_model.eval()
        with torch.no_grad():
            teacher_preds = teacher_model(data)

        # 计算蒸馏后的预测结果
        distillation_loss = soft_loss(
            F.softmax(student_preds/temp, dim=1),
            F.softmax(teacher_preds/temp, dim=1)
        )

        # 将 hard_loss 和 soft_loss 加权求和
        loss = hard_loss_alpha * student_loss + (1-hard_loss_alpha) * distillation_loss

        loss.backward()
        optimizer.step()

    model.eval()
    num_correct = 0
    num_samples = 0
    with torch.no_grad():
        for x, y in test_loader:
            x, y = x.to(device), y.to(device)
            preds = model(x)
            predictions = preds.max(1).indices
            num_correct += (predictions == y).sum()
            num_samples += predictions.size(0)
        acc = (num_correct/num_samples).item()
    print_test(epoch+1, epochs, acc)


# Teacher model train.
# Train epoch: 1/1         step: 1875/1875 [>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>] - loss: 0.21462
# Test  epoch: 1/1         Accuracy:0.9788
# Train epoch: 2/5         step: 1875/1875 [>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>] - loss: 0.06607
# Test  epoch: 2/5         Accuracy:0.9860
# Train epoch: 3/5         step: 1875/1875 [>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>] - loss: 0.04896
# Test  epoch: 3/5         Accuracy:0.9863
# Train epoch: 4/5         step: 1875/1875 [>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>] - loss: 0.04104
# Test  epoch: 4/5         Accuracy:0.9883
# Train epoch: 5/5         step: 1875/1875 [>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>] - loss: 0.03268
# Test  epoch: 5/5         Accuracy:0.9886
# Mini model train.
# Test  epoch: 1/5         Accuracy:0.3423
# Test  epoch: 2/5         Accuracy:0.5190
# Test  epoch: 3/5         Accuracy:0.6088
# Test  epoch: 4/5         Accuracy:0.6365
# Test  epoch: 5/5         Accuracy:0.6584
# Student model train.
# Test  epoch: 1/5         Accuracy:0.3597
# Test  epoch: 2/5         Accuracy:0.5896
# Test  epoch: 4/5         Accuracy:0.6690
# Test  epoch: 4/5         Accuracy:0.7096
# Test  epoch: 5/5         Accuracy:0.7286

数字分类是比较简单的分类，学生模型需要比较弱或差时对比才明显

---

谢谢