【图解】最短路径 Dijkstra 算法

---

作者：Linux猿

简介：CSDN博客专家，华为云享专家，Linux、C/C++、云计算、物联网、面试、刷题、算法尽管咨询我，关注我，有问题私聊！

关注专栏： 数据结构和算法成神路【精讲】优质好文持续更新中……

欢迎小伙伴们点赞、收藏⭐、留言

---

目录

一、什么是单源最短路径?

二、迪杰斯特拉（Dijkstra）算法

2.0 算法起源

2.1 算法原理

2.2 实例演示

2.2 算法模板

2.3 算法复杂度

2.3.1 时间复杂度

2.3.2 空间复杂度

三、迪杰斯特拉（Dijkstra） 实践

四、总结

---

 「迪杰斯特拉（Dijkstra）」算法是图论中常见的一个算法，通常用于求解「单源最短路径」，下面就来看一下。

一、什么是单源最短路径?

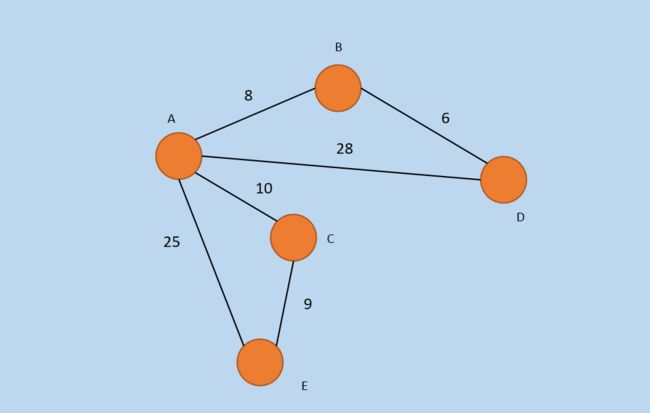
假设有带权无向图 G =（V，E），其中每条边的权是一个实数。另外，还给定 V 中的某个顶点，称为源。要计算从源到图 G 中其他所有各顶点的最短路径长度。这里的长度就是指从源到各顶点的各边权之和，此问题通常称为「单源最短路径」问题。例如图 G 如下所示：

图1 图G

在上图 G 中，假设源为 A，求解以 A 为源的「单源最短路径」，那么，A 到 B、C、D、E的「单源最短路径」分别为：{8， 10, 14，19}。上图中，可以看到，AD的最短路径并非是路径AD，而是A->B->D，同样，AE的最短路径并非是AE，而是A->C->E，这便是最短路径算法的妙用！

我是华丽的分割线

二、迪杰斯特拉（Dijkstra）算法

2.0 算法起源

「迪杰斯特拉（Dijkstra）」算法是由荷兰计算机科学家艾兹赫尔·戴克斯特拉在1956年提出的算法，并于三年后在期刊上发表。「迪杰斯特拉（Dijkstra）」使用类似「广度优先搜索」的方法解决带权图的单源最短路径问题。

2.1 算法原理

假设有图 G = （V，E），其中，V 和 E 分别表示图 G 的顶点和边的集合。

设定两个集合 S 和 Q，分别表示已确定距离源的最短距离的顶点和未确定距离源最短距离的顶点集合。初始时 S = {}，Q = V，同时，维护数组 d 存储所有顶点到源 source 的距离，初始时，

d[source] = 0，表示源点的距离为 0。「迪杰斯特拉（Dijkstra）」算法的步骤如下所示：

（1）从 Q 顶点集合中，选择一个最小 d[u] 值的顶点 u ，u ∈ Q，u 不属于 S，将顶点 u 加入到集合 S 中；

（2）以 u 为中间点，更新 Q 集合中所有顶点到源点 source 的距离，即：source-> u -> v 的距离小于 source -> v 的距离，则更新 d[v] 的值，d[v] 的值表示顶点 v 到源 source 的距离；

（3）继续执行步骤（1）。

2.2 实例演示

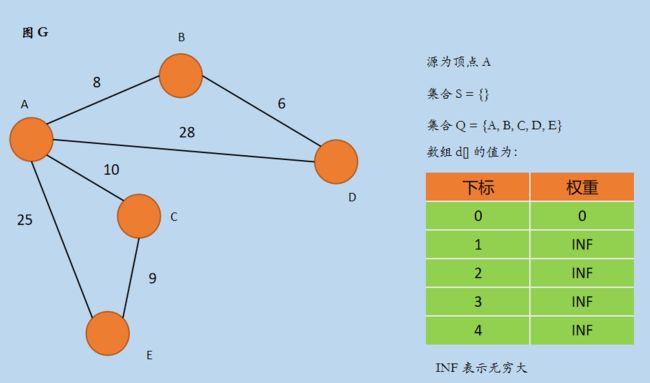
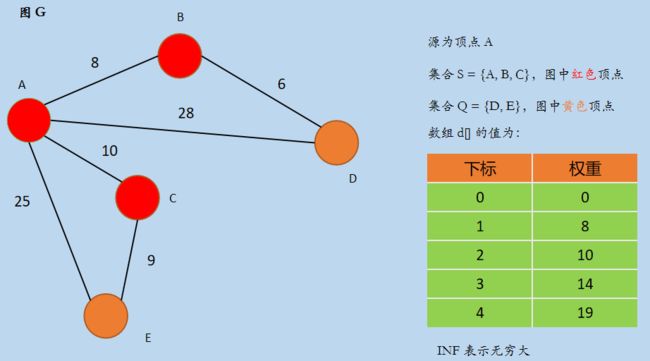
假设有图 G，集合 S = {}，Q = { A, B, C, D, E}，如下所示。 

图2 初始化

  在上图中，初始化后集合 S = {}，Q = {A, B, C, D, E}，d 数组初始化后 d[] = {0, INF, INF, INF, INF}，INF 表示从源不可达。

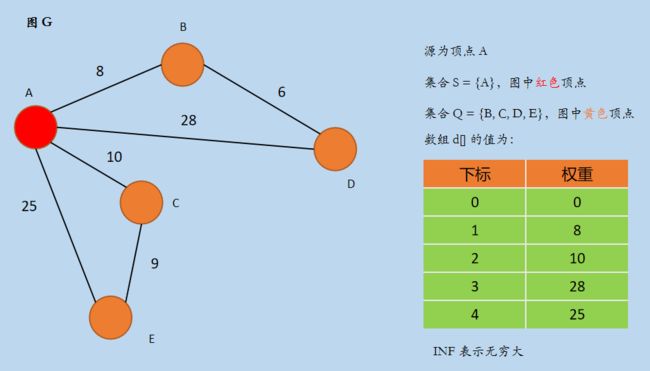
（1）在集合 Q 中寻找一个最小 d[u] 值的顶点 u，此时 u = 0，即顶点 A，A  ∈ Q，且不属于集合 S，将 A 加入集合 S，然后更新数组 d[] 后，如下所示：

图3 选择顶点 A

 选择顶点 A 后，以 A 为中间节点更新集合 Q 中顶点与源 A 的最短距离，更新数组 d 的值为 d[] = {0, 8, 10, 28, 25}，更新了顶点 B, C, D, E 到源 A 的距离。

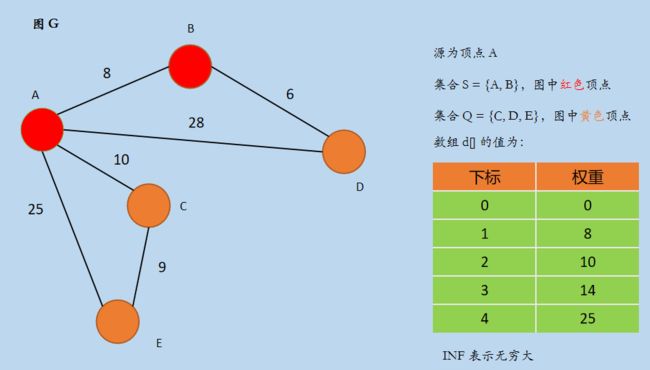
（2）在集合 Q 中寻找一个最小 d[u] 值的顶点 u，此时 u = 1，即顶点 B，B ∈ Q，且不属于集合 S，将 B 加入集合 S，然后更新数组 d[] 后，如下所示：

图4 选择顶点 B

选择顶点 B 后，因为 从 A 经过顶点 B 到达 D 的距离为 14，比直接从 A 到 D 的距离更短，所以 d[3] 更新为 14，其它顶点到源 A 的距离不变。  

 (3) 在集合 Q 中寻找一个最小 d[u] 值的顶点 u，此时 u = 2，即顶点 C，C ∈ Q，且不属于集合 S，将 C 加入集合 S，然后更新数组 d[] 后，如下所示：

图5 选择顶点 C

选择顶点 C 后， 因为 从 A 经过顶点 C 到达 E 的距离为 19，比直接从 A 到 E 的距离更短，所以 d[4] 更新为 19，其它顶点到源 A 的距离不变。

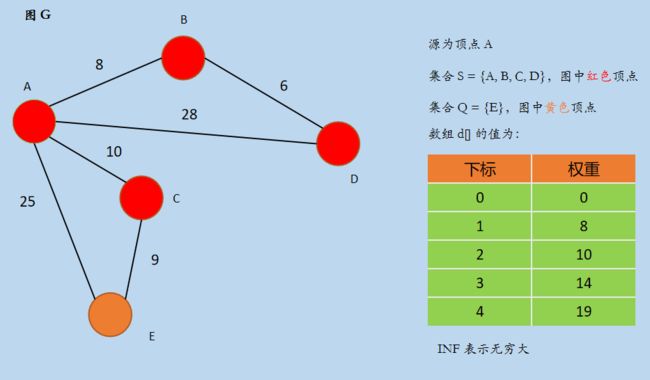
  (4) 在集合 Q 中寻找一个最小 d[u] 值的顶点 u，此时 u = 3，即顶点 D，D ∈ Q，且不属于集合 S，将 D 加入集合 S，然后更新数组 d[] 后，如下所示：

图6 选择顶点 D

 选择顶点 D 后，数组 d[] 无需更新，因为以 D 为中间点无法更新 Q 集合中的 E。

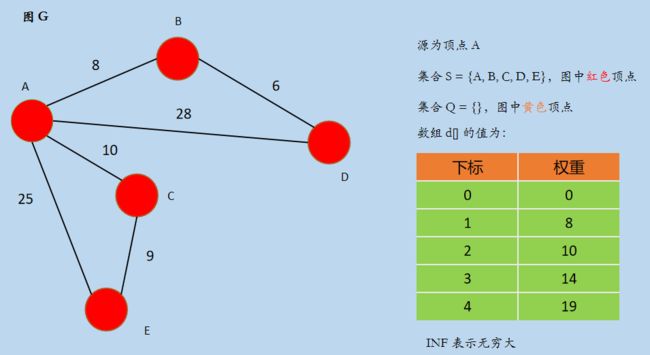
   (5) 在集合 Q 中寻找一个最小 d[u] 值的顶点 u，此时 u = 4，即顶点 E，E ∈ Q，且不属于集合 S，将 E 加入集合 S，然后更新数组 d[] 后，如下所示：

图7 选择顶点 E

选择顶点 E 后，数组 d[] 无需更新。 

经过上面的五步，所有顶点到源 A 的最短距离都已经计算出来了，最终的数组 d[] = {0, 8, 10, 14, 19} ，分别表示源 A 到顶点 {A, B, C, D, E} 的最短距离。

2.2 算法模板

「迪杰斯特拉（Dijkstra）」算法模板如下所示。

#include
#include
#include
using namespace std;
const int MX = 1005;
const int INF = 0x3f3f3f3f;
int n, m;
bool vis[MX];
int d[MX], g[MX][MX];

/***
 * Dijkstra 算法
 */
void dijkstra(int source)
{
    //初始化
    memset(vis, false, sizeof(vis));
    for (int i = 0; i < n; ++i) {
        d[i] = INF;
    }

    d[source] = 0;
    int sx = 0;
    for (int i = 0; i < n; ++i) {
        //寻找距离最近的顶点
        int Min = INF;
        for (int j = 0; j < n; ++j) {
            if (d[j] < Min && !vis[j]) {
              Min = d[sx = j];
          }
        }

        vis[sx] = true; //表示顶点已选中
        //以点 sx 为中间点，更新到源的距离
        for (int j = 0; j < n; ++j) {
            if (d[sx] + g[sx][j] < d[j]) {
                d[j] = d[sx] + g[sx][j];
            }
        }
    }
}

/***
 * 输入边、权重和源
 */
int input() {
    for (int i = 0; i < n; ++i) {
       for (int j = 0; j < n; ++j) {
            g[i][j]=INF ;
        }
    }

    int w;
    char u, v;
    for (int i = 0; i < m; ++i) {
        cin>>u>>v>>w;
        int x = u - 'A';
        int y = v - 'A';
        if (g[x][y] > w) {
            g[x][y] = g[y][x] = w ;
        }
    }

    char source;
    cin>>source;
    return source - 'A';
}
int main()
{
    while (cin>>n>>m) {
        int source = input();
        dijkstra(source);  // source 表示源
        //输出从源 source 到图中其它各点的距离
        for (int i = 0; i < n; ++i) {
            cout<<(d[i] == INF ? -1 : d[i])<<" ";
        }
        cout<

其中， n 表示顶点个数，m 表示边的个数，输入的 u, v, w 表示无向边 (u, v) 的权重为 w。

例如：图1 中「图 G 」的输入样例如下所示：

5 6
A B 8
A D 28
B D 6
A C 10
A E 25
C E 9
A

 输出为：

0 8 10 14 19

2.3 算法复杂度

2.3.1 时间复杂度

时间复杂度为：O(n^2)

在 「2.2 算法模板」 中，「迪杰斯特拉（Dijkstra）」算法主要的时间复杂度在于嵌套的两层 for 循环，所以时间复杂度为 O(n^2)。

2.3.2 空间复杂度

空间复杂度为：O(n^2)

在「2.2 算法模板」 中，「迪杰斯特拉（Dijkstra）」算法主要的空间复杂度为存储顶点和边的关系的二维数组 g，所以空间复杂度为 O(n^2)。

我是华丽的分割线

三、迪杰斯特拉（Dijkstra） 实践

1. MPI Maelstrom

2. Silver Cow Party

我是华丽的分割线

四、总结

本篇文章对算法进行了详解，算法的空间复杂度还可以优化，可以通过邻接表存储边，空间复杂度变为O(n + m)，时间复杂度也可以进一步优化，在每次查找数组 d 中的最小值的时候，可以将这个过程改为最小堆，这样最小堆的时间复杂度为 O(logn)，边存储通过邻接表，所以时间复杂度可以优化到 O(mlogn)。

---

感觉有帮助记得「一键三连」支持下哦！有问题可在评论区留言，感谢大家的一路支持！猿哥将持续输出「优质文章」回馈大家！

---