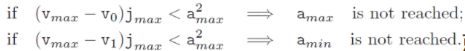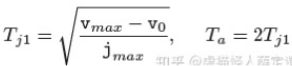【轨迹优化篇】(6)局部运动规划
系列文章目录
提示:这里可以添加系列文章的所有文章的目录,目录需要自己手动添加
TODO:写完再整理
文章目录
- 系列文章目录
- 前言
- 一、规划的方法
-
- 1.轨迹优化设计思想
-
- A、设计代价损失函数进行评分、线性加权法、迹评分轨迹多选一的方法
-
- (1)设计代价函数进行评分、然后选择代价最低的轨迹核心思想
- (2)代价评分的方向
-
- 1.代价函数挑选最优路径
- 2.代价函数初始化节点的代价值
- 3. 一般的代价函数(loss function)的类型(具体公式后续补充)
- 4.通过线性加权的方式计算总代价,挑选出一条整体代价最低的一条局部路径【实现多目标代价】
- (3)应用案例
- (4)总结
- B、梯度下降优化使得轨迹形变方法思想
-
- 一、轨迹优化的泛型过程【约束优化问题】
-
- 1.优化泛型原理
- 2.优化泛型步骤
-
- (1)初始轨迹分段与时间分配【复杂的轨迹一般都是分段轨迹】
- (2)对分段轨迹构建最小目标优化函数,并化简成QP二次规划形式
- (3)根据约束条件构建等式\不等式约束条件方程
- (4)二次规划QP求解器求解并得到最终轨迹
- (5)轨迹评价及轨迹跟踪
- 二、常用的优化算法
-
- 1.基于梯度下降(Gradient)算法
-
- (1)梯度的含义
- (2)梯度的计算方法
- (3)目标函数相关(通过代价使它min最小化)
- (4)约束条件
- (5)梯度下降的过程【梯度和代价就是代价函数】
- (6)优化的相关方法和技巧
- (7)(线性/非线性)优化问题的数学模型理论科普
- (8)理论及编程举例
- 例子一【数学函数的表出】
- 例子二【数学函数的优化】
- 例子三【飞机的轨迹优化】
- 2.基于无梯度(导数)的优化算法
-
- (1)无梯度(导数)的算法的由来
- (2)无梯度(导数)的算法的计算方法
- 3.凸优化的优化算法【这个用OOQP求解器】
- 三、求解优化问题的工具库
-
- 1.nlopt优化库相关
-
- (1)nlopt常用的API
- (2)终止条件
- (3)nlopt的优点
- 2.凸优化求解器类型
- 四、常用目标函数的应用案例
- 五、经验看法
- 六、参考资料
- 2.【多选一】OpenPlanner
-
- 一、OpenPlanner整体效果
- 二、OpenPlanner介绍
-
- 1.OpenPlanner介绍
- 2.OpenPlanner开源框架的特点
- 3.Autoware和OpenPlanner的关系
- 三、OpenPlanner的整体框架及原理
-
- 1.感知模块支持
- 2.地图与定位模块支持
- 3.全局路径规划(分场景使用不同的规划算法)
-
- (1)结构化的环境场景的规划--根据矢量地图选择生成一条全局路径
- (2)非结构化环境场景的规划--根据路径探索生成一条全局路径
- (3)全局路径规划源码分析
- 4.局部路径规划(open_planner)
-
- (1)原理介绍
- (2)Roll-outs Generator【局部路径探索+轨迹优化】
- (3)Roll-outs Evaluator【代价函数挑选最优路径】
- (4)局部路径规划器的跟踪路径
-
-
- (5)局部路径规划源码分析
-
- 四、行为状态生成器【导航决策】
-
- 1、行为状态介绍
- 2、行为状态(也称任务、目标、状态)的定义
- 3、行为状态生成器的作用
- 4、行为状态生成器步骤
- (1)行为状态机的设计
-
- (2)状态机及状态转换条件
- (3)重新规划【结果】
- 五、总结
- 六、参考资料
- 3.lexicographic_planner
-
- 一、lexicographic_planner介绍
- 二、lexicographic_planner的整体流程
-
- 1.路径探索的步骤
-
- (1)伪代码:
- (2)步骤
- 2.路径优化的步骤
-
- (1)代价函数的设计
- (2)通过代价函数挑选最优路径【词袋优化的方法】
-
- 3.lexicographic_planner与open_planner的对比
- 4.lexicographic_planner的效果图
-
- 三、lexicographic_planner源码解读
-
- 1.输入输出
- 2.需要调试的参数
- 3.lexicographc_planner的运行过程
- 4.lexicographic_planner源码解读
- 四、总结
- 五、参考资料
- 4.Teb_planner
-
- 一、Time Elastic Band算法算法核心思想
- 二、Time Elastic Band算法的约束条件
- 三、Time Elastic Band算法多约束的实现
-
- 1.时变弹性带的轨迹模型+footprint机器人模型类
- 2.配置TEB的参数类
- 3.设计约束优化类
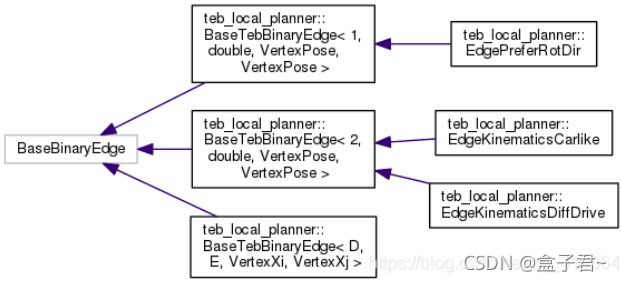
- 4.g2o优化时变弹性带的轨迹类【TebOptimalPlanner】
- 5.局部规划器对外调用的接口类【PlannerInterface】
- 6.将teb_localplanner插件化,使之能被集成到ROS导航包的类【TebLocalPlannerROS】
- 四、Time Elastic Band算法流程(伪代码)
- 五、Time Elastic Band算法部署
-
- (1)Time Elastic Band算法的安装方法
- (2)Time Elastic Band算法的调参使用
- 六、Time Elastic Band算法的优缺点
- 七、总结
- 参考资料
- 二、控制的方法
-
- 1.应激式BUG局部避障算法
-
- (1)应激式BUG算法原理
- (2)应激式BUG算法优点
- (3)应激式BUG算法缺点
- (4) BUG1算法
- (5)BUG2算法
- (6)BUG1和BUG2算法对比
- (7)逻辑方形超声波绕障
- (8)总结
- (9)参考资料
- 2.滑动窗口DWA_planner
-
- (1)DWA_planner算法基本原理
-
- 1.DWA_planner图例
- 2.DWA_planner输入输出
- 3.DWA算法过程(直观理解)
- 4.DWA_planner源码的主要接口及原理
- (2)总结
-
- 1.算法部署方面
- 2.算法思想
- 3.算法缺点
- (3)参考资料
- 3.base_local_planner
-
- (1)(ROS)base_local_planner介绍
- (2)Trajectory Rollout基本算法原理
- (3)(ROS)base_local_planne运行流程
- (4)(ROS)base_local_planner核心函数
- (5)findBestPath()路径探索的核心原理
-
- (0)给定栅格地图Grid Map和全局路径
- (1)TrajectorySampleGenerator接口
- (2)TrajectoryCostFunction接口
- (3)SimpleScoredSamplingPlanner接口
- (4)局部规划器提供支持的一些类
- (5)TrajectoryPlannerROS接口
- 三、曲线的方法
-
- 1.double S直线速度规划
-
- 路径-速度解耦规划
- (1)Double S曲线速度规划介绍
- (2)double S曲线原理及步骤
-
- 1.系统参数定义
- 2.给定曲线的系统参数(假设参数)
- 3.给定曲线的边界参数
- 4.曲线速度、加速度加加速度变化分析及计算【通过控制时间实现】
-
- 情况1 :曲线的终点大于起点,即曲线是向前进的(q1>q0)
- 情况2 :曲线的起点大于终点,即曲线是向后退的(q0>q1)
- 5.控制输出
-
- 加速段控制率
- 匀速段控制率
- 减速段控制率
- (3)程序流程图
- (4)二维源代码示例
- (5)三维的源代码解析示例
-
- double S曲线的类及其参数
- double S曲线计算【单段曲线】
- 【核心--调用】输入当前时间,获取曲线的当前位置点,曲线调用的方式和B样条如出一辙
- 获取double S曲线的运行总时间
- (6)总结
- (7)参考资料
- 四、【地图的方法】
-
- 1、局部路径规划VFH、VFH+、VFH*算法(输入是局部栅格地图,输出下一步的运动方向)
-
- (0)人工势场算法入门
-
- 一、算法思想
- 二、算法的输入输出
- 三、算法流程
- 四、人工势场的改进
- 五、算法效果
- (1)Virtual Force Field (VFF)算法
-
- 1、主要的步骤
- 2、VFF算法问题
- (2)VFH算法--用地图的方法做运动规划
-
- 1.VFH算法的中心思想--把栅格图转换成统计直方图的地图格式
- 2.VFH的3层数据及数据转换步骤
-
- (1)VFH的3层数据
- (2)数据转换步骤
- 3.VFH应用上的局限
- 4.VFH的优点
- 5.代码实现
- (3)VFH+算法
-
- 1.VFH+算法的实现步骤
- 2.VFH+算法的优点
- 3.VFH+算法应用中主要有2个问题
- 4.代码实现
- (4)VFH*算法
-
- 参考资料
- 总结
- 参考资料
前言
认知有限,望大家多多包涵,有什么问题也希望能够与大家多交流,共同成长!本文先对**【轨迹优化篇】局部运动规划**做个简单的介绍,具体内容后续再更,其他模块可以参考去我其他文章
提示:以下是本篇文章正文内容
一、规划的方法
1.轨迹优化设计思想
A、设计代价损失函数进行评分、线性加权法、迹评分轨迹多选一的方法
(1)设计代价函数进行评分、然后选择代价最低的轨迹核心思想
若是有多条候选的局部路径,进行轨迹选择
(1)这种方法【防盗标记–盒子君hzj】并没有用到优化理论的知识–本质是从多选优
(2)更好的多准则问题,通常是考虑了时间、能量、行进距离、碰撞、交通规则等更多约束的路径
.
.
(2)代价评分的方向
1.代价函数挑选最优路径
在采样节点的形成搜索树/搜索图时候,【防盗标记–盒子君hzj】对搜索树/搜索图的边赋予代价信息
.
.
2.代价函数初始化节点的代价值
在采样节点的形成搜索树/搜索图时候,【防盗标记–盒子君hzj】对搜索树/搜索图的节点赋予代价信息
.
.
3. 一般的代价函数(loss function)的类型(具体公式后续补充)
(2)子代价函数的考虑可能结合以下因素
路径长度、曲率平滑度、速度平滑度、车辆偏离车道中心线(目标位置距离)、与障碍物的距离、安全性、对车辆的压力等等。
举例:换道路径曲线的筛选原则–曲率
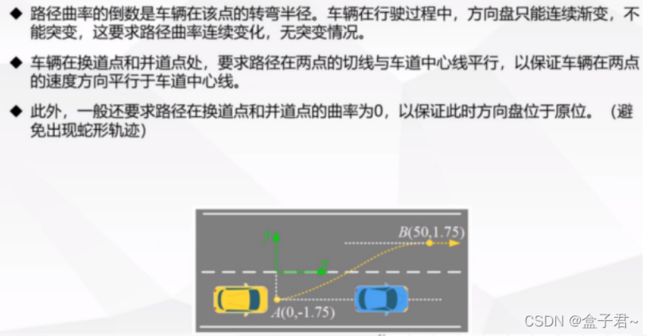

.
(1)L2 loss代价函数
![]()
(4)Barrir loss代价函数

(5)单项式函数
(1)绝对值平方V型函数(优化函数)
(2)二元一次抛物线函数(优化函数)
(3)一元二次直线函数(优化函数)
(4)更复杂的优化函数…(建议看看TEB的五个目标函数)
(6)多项式函数
把多个单项式函数累加起来,并为每个项赋予一个权重
4.通过线性加权的方式计算总代价,挑选出一条整体代价最低的一条局部路径【实现多目标代价】
比例分权方法求总的代价【本质用在最优控制中的多准则问题】,比例分权方法的一般套路如下:

(3)应用案例
(1)矢量地图路线的选择评分
(2)open_planner的路径评分
(3)DWA的路径选择评分
(4)总结
1、工程常用方法:线性加权法–如上面的计算路径长度和路径平均曲率两个目标的代价
线性加权法并没有用到优化的知识–从多选优
2、学术常用方法:利用了优化理论的NSGA、Pareto最前沿
.
.
B、梯度下降优化使得轨迹形变方法思想
一、轨迹优化的泛型过程【约束优化问题】
1.优化泛型原理
轨迹优化问题通常建模成一个带约束的二次规划(QP)问题来求解。其中:
1)优化函数可以是snap、jerk、acceleration【防盗标记–盒子君hzj】及它们的组合或其他任何能够formulate成Qp形式的函数(通常满足约束条件的轨迹有无数条,而实际问题中,往往需要一条特定的轨迹,所以又需要构建一个最优的函数,在可行的轨迹中找出“最优”的那条特定的轨迹。)
2)约束条件包括等式约束条件和不等式约束条件
尽量满足约束条件下,使用优化的方法最小化目标函数,进而求目标函数(即轨迹的多项式的参数p1,…,pk
注意:
最要命的是优化函数或者约束条件是非线性甚至是非凸的,【防盗标记–盒子君hzj】复杂一点点的优化函数或约束条件就是凸优化寻找最值的方式,更复杂的是非凸优化寻找极值的方式
2.优化泛型步骤
(1)初始轨迹分段与时间分配【复杂的轨迹一般都是分段轨迹】
1)轨迹分段:根据路径点,将轨迹分为k段,计算每段的距离
2)分段轨迹的时间分配
时间分配是轨迹规划中很关键的一个问题,它直接影响规划结果的好坏,可根据每段的距离或者其他要求将总时间T分配到每段
(1)总时间给定
(2)各段时间分配
1)匀速分配方法
假设每段polynomial内速度恒定不变,【防盗标记–盒子君hzj】这样各段poly的时间比就等于路程比
2)梯形分配方法
假设每段polynomial内速度曲线以恒定加速度a从0加速到最大速度vmax,再以−a减速到0。a和vmax事先给定,就能得出每一段所需要的时间。
设各段时间分别为t′1,t′2,…,t′n,求前k项和可以得到轨迹分段的时刻向量
t0=0
t1=t′1
t2=t1+t′2
,…,
tn=tn−1+t′n
3)对x,y维度单独规划轨迹
.
.
(2)对分段轨迹构建最小目标优化函数,并化简成QP二次规划形式
将轨迹规划问题建模(fomulate)成一个约束优化问题,通过最优化的方法求解出目标轨迹参数 p
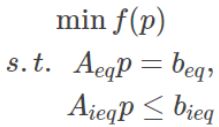
做法:将优化问题中的f§函数和Aeq,beq,Aieq,bieq参数给列出来,然后丢到优化器中求解轨迹参数p
注意:【防盗标记–盒子君hzj】这里的轨迹参数p是多段polynomial多项式组成的大参数向量 p=[pT1,pT2,…,pTk]T
Minimum Snap中的最小化目标函数是Snap(加加加速度),当然你也可以最小化Acceleration(加速度)或者Jerk(加加速度),至于它们之间有什么区别,quora上有讨论。一般不会最小化速度
.
.
(3)根据约束条件构建等式\不等式约束条件方程
我们希望轨迹满足一系列的约束条件【根据规划的要求】
约束举例如下:
(1)约束1:希望设定起点和终点的位置、速度或加速度
(2)约束2:希望可以设定在途中机器人的最大速度、最大加速度
(3)约束3:希望相邻轨迹连接处平滑(位置连续、速度连续等)
(4)约束4:希望轨迹经过某些路径点
(5)约束5:希望轨迹在规定空间内(corridor)
(6)约束6:希望轨迹在可行通道corridor内
为了限制轨迹的形状,引入了corridor的概念,corridor可以理解为可行通道,如下图,规划出的轨迹必须在corridor内。直观的思路是:如果能把corridor当作约束加入到QP问题中,那么解得的轨迹自然就在corridor内了
构造corridor不等式约束
为了方便构造,对于每一个采样点pt,我们施加一个矩形的corridor,【防盗标记–盒子君hzj】即
![]()
这里用矩形corridor是因为斜线corridor(平行四边形)不好构造,而且我们只需要大致在corridor里面就好,没有必要非弄一个严格的斜线corridor。对于每个采样点,设矩形corridor的边长为 2r,增加两个位置不等式约束:

上述是位置corridor,也就是位置不等式约束,但同样也可以扩展到速度corridor、加速度corridor乃至更高阶
.
.
(4)二次规划QP求解器求解并得到最终轨迹
【闭式求解】
如果QP问题只有等式约束没有不等式约束,【防盗标记–盒子君hzj】那么是可以闭式求解(close form)的。闭式求解效率要快很多,而且只需要用到矩阵运算,不需要QPsolver
【非闭式求解】
利用QP求解器进行求解,在MATLAB中可以使用quadprog() 函数,C++的QP求解器如OOQP
(5)轨迹评价及轨迹跟踪
.
.
二、常用的优化算法
1.基于梯度下降(Gradient)算法
(1)梯度的含义
梯度就是(偏)导数的意思,两个位置的导数就是方向,【防盗标记–盒子君hzj】梯度按通俗的意思来讲就是 参数x变化的方向和大小
(2)梯度的计算方法
一般通过计算(偏)导数的方法来计算梯度。例如 min(lnx1-lnx2),x1的梯度就是1/x1,x2的梯度就是-1/x2.
(3)目标函数相关(通过代价使它min最小化)
目标函数的目的是计算cost和grad-实现梯度下降的模板
目标函数就是提供计算代价cost和梯度grad的方法,使得在一次一次的迭代中cost在沿着grad下降的方向不断减小–梯度下降的原理
优化器中目标函数costfunction的cost就是欧式距离、【防盗标记–盒子君hzj】grad就是梯度方向,这样就可以建立理论桥梁的,推导出目标函数都是用几何的方法计算欧氏距离和梯度
数学模型及目标函数关系
数学模型f(x)=sinx1+cosx2,取f(x)的最小值可以表达成目标函数min(sinx1+cosx2)
.
目标函数的设计
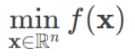
其中 f 是目标函数,x表示n个 优化参数(也称为设计变量或决策参数)
(1)类型一:多元连续函数(可以用公式表出)
(2)类型二:多项式离散函数(不可以用公式表出,处理的时候对子项处理,权重累加)
在整个优化器中,仅仅只有一个目标函数,但是这个目标函数是由多个优化项组成的【一般的目标函数是可以用连续函数表出的,但是在工程中多是使用离散工程的方式计算子cost,【防盗标记–盒子君hzj】再通过权重weight把每个子cost连接起来】
优化理论需要看一看
(1)怎么建立优化理论和实际模型的桥梁
(2)目标函数编程怎么写?
优化的目标函数要分类一下,积累常用效果的目标函数就好
设计目标函数是一个技术活,工程实现求解是一个技术活
(4)约束条件
满足所有边界约束、不等式和等式约束的点x称为可行点,【防盗标记–盒子君hzj】所有可行点的集合为可行区域
优化的时候可以没有约束条件,没有约束条件就是相当于约束条件是无穷大.约束条件一般都要有,不然找不出极值
【约束条件的类型可以是下面三种类型的组合】
(1)边界约束【也称为box约束】
目的:求极值时的参数的范围限幅
公式:给定下限lb和上限ub(对于部分或完全无约束的问题分别为-∞和/或+∞)
![]()
(2)非线性不等式约束
目的:求非线性不等式约束的范围限幅,【防盗标记–盒子君hzj】一个参数也可以选择具有m个非线性不等式约束(有时称为非线性规划问题)
公式:

(3)非线性等式约束
目的:一些NLopt算法还支持p个非线性等式约束
公式:
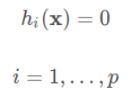
(5)梯度下降的过程【梯度和代价就是代价函数】
(1)梯度下降解决什么问题?
梯度下降的方法实现路径的优化!
优化器计算出一个cost和grad之后怎么让一个路径进行形变呢?[通过nlopt的内置梯度下降的方法]
.
(2)梯度下降的过程
一条路径可以看成一系列的控制点x,每个控制点都有自身的cost(欧式距离)和grad(梯度),nlopt优化库对总的目标用函数costfunction进行一轮一轮的迭代(costfunction()内置的子costfunction()输出的子cost和grad会根据各自权重叠加成一个和总的cost和grad)【防盗标记–盒子君hzj】,总的cost和grad输入nlopt的API后就会再nlopt内部实现梯度下降,梯度下降的过程就是路径点沿着梯度grad下降的方向final_cost值不断减小,逐渐达到极小值,梯度下降在一轮一轮迭代中路径点x逐渐最优的过程,经过nlopt内部实现的梯度下降,最终nlopt在形参中返回最优(形变)的路径点x,同时也可以通过API读取到opt执行梯度下降过程中的final_cost,final_cost没有实际意义仅仅用于调试过程查看cost值有没有减小【防盗标记–盒子君hzj】,真正有用的是输出优化形变后的优化因子(路径点)
所以说,梯度下降仅仅是一个盒子的过程,对于优化器,我们仅仅需要输入目标函数costfunction【要设计】、约束条件【要设计】、终止条件【要设计】、还有应优化因子(路径点);获取输出的优化过后的优化因子(路径点)和用于调试的final_cost就行
梯度下降的实现过程是在nlopt一轮一轮迭代过程中实现的
.
(6)优化的相关方法和技巧
优化的方法一般都是用二次项的方式,因为二次项的方式比较简单,也比较容易添加多个优化项,其次就是用共轭梯度下降的方式,复杂一点点就是凸优化寻找最值的方式,【防盗标记–盒子君hzj】更复杂的是非凸优化寻找极值的方式
优化的技巧是
(1)限定优化的迭代次数
(2)限定优化所使用的时间
(3)用优化库来实现
(7)(线性/非线性)优化问题的数学模型理论科普
0)线性/非线性/凸优化优化定义
(1)线性优化定义
线性函数是最简单的,单调增或者单调减,那么找到边界就可以求到极值。例如 f(x)=ax+b
(2)非线性优化定义
对于复杂的非线性函数,或者复杂的数学模型,求导很困难或者无法求导的时候就使用非线性优化的知识了
通俗一点来说,非线性优化就是求函数的极值,【防盗标记–盒子君hzj】在非线性优化里面通常求最小值,如果你求最大值就是在优化前给函数加个负号
(8)理论及编程举例
例子一【数学函数的表出】
(1)数学模型
数学模型f(x)=sinx1+cosx2,取f(x)的最小值可以表达成目标函数min(sinx1+cosx2)
(2)约束条件
1)边界约束【也称为box约束】:2< x1 <10 ,同时满足3
3)非线性等式约束:x1+x2=1
例子二【数学函数的优化】
(1)数学推导
1)示例图

2)数学模型及目标函数
![]()
这个是目标函数 求满足 条件的情况下 x2的开平方最小
3)约束条件
边界约束:
![]()
非线性不等式约束:
![]()
有两个参数 x1 和 x2 ,其中 a和b是模型的参数可以设为任意的固定值,这个模型设为a1=2,b1=0,a2=-1,b2=1
(2)编程实现
1)目标函数编程
![]()
的编程实现(主要是计算目标函数f(x)代价值及目标函数的梯度(目标函数的变化方向))
double myfunc(unsigned n, const double *x, double *grad, void *my_func_data)
{
if (grad) {
grad[0] = 0.0;
grad[1] = 0.5 / sqrt(x[1]);
}
return sqrt(x[1]);
}
(1)myfunc时定义的函数的名字可以随意改,后面的参数基本不要动,就是这么个形式的
(2)n代表待优化的因子个数
(3)x是待优化的参数向量
(4)grad 是梯度,grad[0]附值对应x[0]的偏导数,grad[1]附值对应x[1]的偏导数,对于基于梯度的算法,则在目标函数里面需要给grad赋值
(5)my_func_data 是外部参数用于数学模型中的,如果没有,就不用
(6)返回值要是 你的 目标函数
2)约束条件编程
方法:不等式约束相当于参数不同的一样的约束方程来进行编程
非线性不等式约束(描述约束条件函数及其梯度(偏导数))
![]()
对于每个不等式约束我们需要传入a和b的值,创建一个结构体
typedef struct {
double a, b;
} my_constraint_data;
double myconstraint(unsigned n, const double *x, double *grad, void *data)
{
//声明对应外部数据刚定义的结构体 数据 然后赋值就可以了
my_constraint_data *d = (my_constraint_data *) data;
//获得a和b
double a = d->a, b = d->b;
if (grad) {
grad[0] = 3 * a * (a*x[0] + b) * (a*x[0] + b);//对x0求偏导
grad[1] = -1.0;//对x1求偏导
}
return ((a*x[0] + b) * (a*x[0] + b) * (a*x[0] + b) - x[1]);//返回 不等函数
}
函数的形参和目标函数一致
3)创建nlopt优化器
(1)创建nlopt_opt 类的 对象
nlopt_opt opt;
(2)设置算法和维度
opt = nlopt_create(NLOPT_LD_MMA, 2);
//设置算法和维度 算法有很多种选择 , 维度就是 x的个数,优化因子个数
(3)声明优化因子x的下限
【注意优化因子是一个列表,因为目标函数有可能是多元的】
【数学模型里面没有上限,可以不设置,默认为无穷大】
double lb[2] = { -HUGE_VAL, 0 }; // 第0个元素代表x[0] 第1个元素代表x[1]
nlopt_set_lower_bounds(opt, lb);//设置x的下限
(4)声明x的上限
double lb[2] = { 5, 10 }; // 第0个元素代表x[0] 第1个元素代表x[1]
nlopt_set_upper_bounds(opt, lb);//设置x的上限
(5)设置目标函数
nlopt_set_min_objective(opt, myfunc, NULL);
//设置目标函数 ,第二个参数就是上面定义的目标函数的函数名,第三个参数是外部参数,因为没有,则为NULL
(6)添加约束条件
my_constraint_data data[2] = { {2,0}, {-1,1} };//不等式的外部参数 上面定义的结构体
nlopt_add_inequality_constraint(opt, myconstraint, &data[0], 1e-8);//不等式约束1
nlopt_add_inequality_constraint(opt, myconstraint, &data[1], 1e-8);//不等式约束1
第二个参数是不等式约束的函数名
第三个参数是外部参数
第四个参数1e-8是很重要的,叫做约束的容差,如果一个点满足,不等函数>-(1e-8)那这个点也不采用。这样做是出于收敛的目的,避免微小的偏差导致不能收敛
(7)终止条件
nlopt_set_xtol_rel(opt, 1e-4);//设置x的绝对容差
(8)调用 nlopt_optimize()函数执行优化,实现梯度下降
double x[2] = { 1.234, 5.678 }; /* x的初始值 */
double minf; /* 计算的最小值存入的变量 */
if (nlopt_optimize(opt, x, &minf) < 0) {
printf("nlopt failed!\n");
}
else {
printf("found minimum at f(%g,%g) = %0.10g\n", x[0], x[1], minf);
}
如果优化失败,nlopt_optimize函数会返回负值
失败的原因一般是 传递无效参数、内存不足或类似情况
(9)查询迭代次数
如果想要知道迭代次数,那么可以在定义的目标函数里面加入一个自增1的变量
int count = 0;
double myfunc(int n, const double *x, double *grad, void *my_func_data)
{
++count;
if (grad) {
grad[0] = 0.0;
grad[1] = 0.5 / sqrt(x[1]);
}
return sqrt(x[1]);
}
(10)调用 nlopt_destroy 来结束优化
nlopt_destroy(opt);
例子三【飞机的轨迹优化】
(1)核心思想
(1)输入:要进行优化的控制点points、优化的时间间隔ts,优化项cost_function,最大的迭代次数max_num_id、最大的优化时间max_time_id、一开始不需要进行优化的控制点数量
(2)输出:使用nlopt优化库进行优化,输出优化过后的控制点points
目标函数是一个多项式的函数,每个子项都会根据优化需求计算自己的代价cost和梯度grad【在路径规划中,代价cost的一般是欧式距离,梯度一般是esdf地图的梯度】
(2)步骤
1)设计相关的代价目标函数【计算代价cost和梯度grad】
1、子目标函数的设计
(1)平滑度代价函数calcSmoothnessCost()
核心原理:jerk平滑取极值,即是求加加速度的距离代价cost和梯度
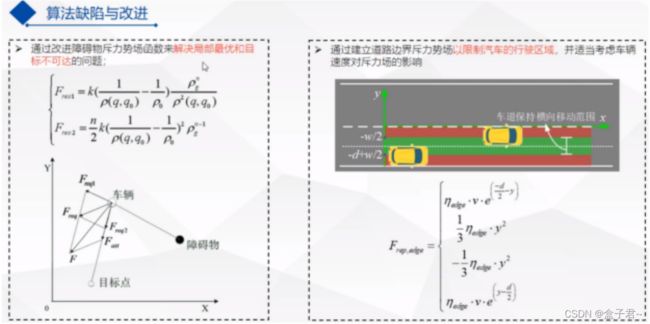
(2)远离障碍物代价优化calcDistanceCost()
核心原理:直接用esdf地图数据来填充【若是TEB算法用代价地图的,实现可能不一样,但是原理是一样的】
(3)计算速度、加速度可行性代价函数calcFeasibilityCost()
核心原理:计算飞机现在的速度和加速度有没有超过阈值,若超过计算对应的grad和cost(几何的方式算)
(4)计算最后一个吻合程度代价函数
核心原理:终点非均值滤波后得到的终点和理想终点的差值,通过二范数计算距离 cost=xx + yy
(5)计算路径点贴合的代价函数
核心原理:非均值滤波后得到的路径点和理想路径点的差值,通过二范数计算距离 cost=xx + yy
(6)计算路径点引导的代价函数
核心原理:使用几何路径上的均匀采样点引导轨迹。对于每个要优化的控制点,在路径上为其指定一个引导点,并对它们之间的距离进行惩罚
(2)总的目标函数-combine所有的子目标函数
每个子目标函数都有对应的权重,把每个子子目标函数看成一个项,累加到一起就行了
(2)进行优化操作optimize()【使用了nlopt优化库】
(1)初始化优化器参数并计算优化变量的数目initialize solver
(2)使用NLopt库进行优化
1)使用nlopt库创建一个优化器opt,并进行相关API的设置
【包括目标代价函数类型、约束条件(最大的迭代次数、最大的优化时间)、停止条件】
2)遍历所有的控制点,并把所有的控制点放入中间变量q中
【后面就是对这个中间变量q进行优化的】
3)nlopt优化库设定优化变量上下边界
4)开始优化nlopt的优化
5)得到最优的控制点control_points_
(3)返回优化后的控制点control_points_
.
.
2.基于无梯度(导数)的优化算法
(1)无梯度(导数)的算法的由来
计算梯度有的时候是很困难的。那么有的优化模型在不使用的梯度的时候可以求解出来,就有了无导数算法
(2)无梯度(导数)的算法的计算方法
该算法仅要求用户提供给定点x的函数值 f(x),这种方法通常必须对f进行至少几倍n点的计算。n就是x的个数。当x的个数不是很多的时候,可以使用这种方法。不用求梯度了就
【注意!!!】对于无导数算法的,不需要计算导数,grad应该是NULL
.
.
3.凸优化的优化算法【这个用OOQP求解器】
(1)在特殊类别的问题中,目标和不等式约束函数都是 (并且等式约束是,或者在任何情况下都具有凸水平集),因此只有一个局部最小值f,因此局部优化方法能找到一个全局最优解。但是,可能会有不止一个点x产生相同的最小值f(x),最优点形成(凸)可行区域的凸子集。
(2)通常,凸问题是由特殊分析形式的功能引起的,例如线性规划问题,半定规划,二次规划等,并且可以使用专门的技术非常有效地解决这些问题。
(3)NLopt仅包含 不假定凸性的常规方法;如果您遇到了凸的问题,最好使用其他软件包,例如Stanford 的
三、求解优化问题的工具库
1.nlopt优化库相关
(1)nlopt常用的API
【不同版本的nlopt的API名字可能不太一样,但是原理流程都是差不多的】
nlopt_create
nlopt_set_min_objective
nlopt_set_lower_bounds
nlopt_add_inequality_constraint
nlopt_set_stopval
nlopt_minimize_econstrained
return value
(2)终止条件
(1)终止条件定义
算法都是通过迭代的方式不断计算下去,通过比较得到优化的点,终止条件就是计算的时候什么情况下停下
(2)NLopt也提供了不同的终止条件选择
(1)迭代次数和时间
设置最大的迭代次数,或者计算时间,来控制优化的停止
(2)函数值停止数值
通过设定优化达到的函数值为一个固定值时,优化停止
这种停止方法对于 comparing algorithms (一种非线性优化算法)更有效果。在长时间运行一种算法以找到所需精度的最小值后,您可以询问算法需要多少次迭代才能获得相同精度或更高精度的最优值
(3)函数值容差和参数容差
在函数的计算值上指定 分数容差(ftol_rel)和绝对容差(ftol_abs) 当 df/f%26lt;ftol_rel 或者 df%26lt;ftol_abs 时停止
同样可以在参数x上指定 分数容差(xtol_rel)和绝对容差(xtol_abs) 当 dx/lt;xol_rel 或者 dx/lt;xtol_abs 时停止
通常情况下,分数容差会更有用,因为它独立于任何绝对比例因子或单位
当你认为 函数最小值或 参数最优点在0附近时,那么绝对容差时有用的
(3)nlopt的优点
【nlopt一般是用来解非线性优化问题的,一般是实现梯度下降的方法】
(1)处理基于约束的优化(等式、不等式、有界等不同的约束极值)、参数的优化的问题
(2)对一个问题尝试不同的算法,调整一个参数就行
(3)支持全局优化和局部优化
(4)支持常见的需要导数和不需要导数的多种算法
2.凸优化求解器类型
(1)CVX【不太兼容】
http://cvxr.com/cvx/
Matlab wrapper. Let you write down the convex program like mathematical equations, then call other solvers to solve the problem.
(2)Mosek【学术用】
https://www.mosek.com/
Very robust convex solvers, can solve almost all kinds of convex programs. Can apply free academic license. Only library available (x86).
(3)OOQP【非常好但是优点老】
http://pages.cs.wisc.edu/~swright/ooqp/
Very fast, robust QP solver. Open sourced.
(4)GLPK
https://www.gnu.org/software/glpk/
Very fast, robust LP solver. Open sourced
四、常用目标函数的应用案例
1.【MinimumJerk轨迹生成与优化】优化目标函数是加加速度函数
2.【MinimumSnap轨迹生成与优化】优化目标函数是加加加速度函数
3.【TEB_Planner】优化目标函数是多项式函数
五、经验看法
共轭梯度下降的方法其实也是代价函数优化的方法,只是两个优化项是共轭的
优化的实现一般都是用库,知道对应的库有什么用和怎么用就行
六、参考资料
(1)链接
https://www.guyuehome.com/35109
https://zhuanlan.zhihu.com/p/24350637
https://vimsky.com/examples/detail/python-method-nlopt.opt.html
https://blog.csdn.net/yy3620285/article/details/79803155
https://www.cnblogs.com/GuanghuiLiu/p/9967684.html
https://www.cnblogs.com/luoyinjie/p/11288095.html
https://blog.csdn.net/weixin_43830248/article/details/102679362
https://blog.csdn.net/potxxx/article/details/80743146
(2)基于函数优化的方法:Functions Optimization
![]()
![]()
(3)梯度下降的官方网站
https://en.wikipedia.org/wiki/Gradient_descent
2.【多选一】OpenPlanner
一、OpenPlanner整体效果
![]()
二、OpenPlanner介绍
1.OpenPlanner介绍
规划执行最优路径,同时避免障碍,触发行为例如在交通信号灯处停车
2.OpenPlanner开源框架的特点
(1)OpenPlanner框架足够通用,可剪裁才增加,【防盗标记–盒子君hzj】只需调整其参数即可与任何移动机器人配合使用
(2)OpenPlanner更适合于遵守交通规则的自主移动机器人导航系统,更适用于车道线场景的自动驾驶领域,OpenPlanner通用性强,只需相应的调整参数即可部署在一台新的无人驾驶车上
(3)OpenPlanner它结合了矢量地图或道路网络地图中包含的所有离散信息(例如交通信号灯,交通标志,十字路口,停车线等的位置),这相对于其他的开源的导航系统OMPL和Navigation Stack来说是主要的优势
事先有一张矢量地图,车载还有激光雷达和相机的detector模块
(4)OpenPlanner不完全适合杂乱无章的农业场景,【防盗标记–盒子君hzj】需要改造,这里就是论文的切入点,农业场景它仅需要矢量地图和目标位置即可进行全局规划,而对于局部规划和行为状态生成,则仅需要当前位置和检测到的障碍即可
3.Autoware和OpenPlanner的关系
Autoware是ROS软件包的集合,包括OpenPlanner,以及其他功能包
.
三、OpenPlanner的整体框架及原理
![]()
1.感知模块支持
通过相机detect,得到障碍物信息(detected obstacles)、交通标志(traffic light color)等
.
2.地图与定位模块支持
通过SLAM和定位模块提供到高清矢量地图(vector_map)【防盗标记–盒子君hzj】(基于用传感器信息更新的代价地图)和高精度定位信息(goal_pose、start_pose、current_pose)
.
3.全局路径规划(分场景使用不同的规划算法)
目的:全局路径规划的分场景的,不同的场景用不同的路径规划算法,最终得到一条静态的全局参考路径
(1)结构化的环境场景的规划–根据矢量地图选择生成一条全局路径
1)场景
在结构化环境中,我们必须遵循交通规则,例如在车道中心驾驶,向正确的方向行驶,仅在被允许进入正确的车道以向右转或向左转时才可改变方向,在该环境中我们可以清楚地定义道路,行车线,十字路口等,以及交通标志,所有这些都可以在矢量地图中进行描述。
2)规划方法
仅仅用到vector_map就可以实现全局的路径规划,open_planner的全局路径是从vector_map上得到的,,当然矢量地图中有多条lane车道,在哪条lane车道形式还是要用图搜索的方法确定,【防盗标记–盒子君hzj】遇到障碍物的时候截取一段做局部路径规划
常用的算法类型:A*算法、Dijkstra算法
使用(A*算法)找到从当前位置到目标所有的可能路线。【防盗标记–盒子君hzj】 在路线跟踪过程中,我们构建了可能的路径树,遵循矢量地图定义的规则,直到车辆到达目标为止,一旦达到目标,便会追踪从目标到起始位置的路线,进而选出唯一全局参考路径
![]()
在地图上搜索最短路径。 线条颜色表示路线代价
.
.
.
(2)非结构化环境场景的规划–根据路径探索生成一条全局路径
非结构化环境场景包括自由空间的平地场景、越野驾驶场景、停车泊车场景,即我们无法使用矢量地图的位置
使用向量图可以更轻松,更快地进行全局和局部规划。【防盗标记–盒子君hzj】当然,像RRT * 和Hybrid A *这样的自由空间全局规划器对于停车和越野情况都很重要。在这种情况下,我们可以切换到自由空间规划器进行全局规划,而仍然使用Open Planner的行为状态机和本地规划器
常用的算法类型:RRT * 和Hybrid A *
.
.
(3)全局路径规划源码分析
待补充
4.局部路径规划(open_planner)
(1)原理介绍
将高清矢量地图和定位数据作为先验信息输入,在全局中,指定一个起点,一个终点,通过全局规划得到一条全局静态路径,全局路径规划在车辆启动或重启的时候被确定,一旦分配了全局路径,本地马上启动运动规划器
根据静态的全局参考路径,采用轨迹生成算法Roll-outs Generator,得到局部多条平滑的采样轨迹(候选的一系列轨迹用到了共轭梯度下降轨迹优化平滑的方法),【防盗标记–盒子君hzj】再通过障碍物检测与代价函数Roll-outs Evaluator方法计算每条采样轨迹的归一化代价函数,挑选一条代价最低且局部最优路径。最后通过纯跟踪算法将规划出来的轨迹用于实际控制
op_planner的local_planner主要分为两部分:Rollouts Generator 和 Rollouts Evaluator
(2)Roll-outs Generator【局部路径探索+轨迹优化】
1)作用
Rollouts 的含义就是根据中心全局路径生成的一些列候选局部路径,Rollouts Generator根据全局中心路径生成一系列平滑的候选局部路径
根据矢量地图生成的全局路径作为参考生成一系列平滑的候选路径
2)确定输入输出
候选路径生成算法的输入是当前位置、规划距离、【防盗标记–盒子君hzj】生成候选路径的数量和全局路径。输出为n条平滑轨迹,从车辆中心一直延伸到最大规划距离
3)确定规划区域
![]()
(1)Car tip:从车辆中心到横向采样点的距离,其长度决定了车辆切换到不同轨迹的平滑度
(2)Roll in:水平横向采样点到平行横向采样点的距离,其长度与车辆速度成正比。车辆行驶的速度越快,此区域产生平滑变化的时间就越长
(3)Roll out:平行横向采样点到最大规划距离,通过从全局路径垂直移动固定的距离(称为Roll out密度)来执行直接横向采样
4)Roll-outs Generator三个主要步骤
![]()
(1)根据车辆的当前位置和最大规划距离从全局路径中提取所需的car tip、Roll in、Roll out三个部分;
(2)针对提取出的全局路径进行点的横向采样;对与全局路径的提取的三个部分相对应的新的垂直航路点进行采样。 采样从横向距离为零的车头边缘开始,然后逐渐增加,【防盗标记–盒子君hzj】以达到在滚动边际末尾使用每个轨迹指数计算得出的滚动密度。
(3)使用共轭梯度对每个采样轨迹进行平滑处理生成候选轨迹,共轭梯度是一种非线性迭代优化技术,可消除采样步骤导致的滚动不连续性。 这也改善了曲率,从而使转向更平稳
.
(3)Roll-outs Evaluator【代价函数挑选最优路径】
1)轨迹选择图例
![]()
2)作用
结合障碍物信息和其他因素计算各个Rollout的优先级代价、【防盗标记–盒子君hzj】过渡代价和碰撞代价评估每一条从Roll-outs Generator生成的候选路径,从而挑选出一条平滑、无障碍的局部路径
3)障碍物检测
(1)边界框检测方法
通过使用边界框,我们可以显着提高障碍物检测性能,但会牺牲准确性
(2)点云数据簇检测方法【推荐】
使用点云数据可以大大提高检测精度,仅使用点云数据簇的轮廓点样本来解决性能降低问题,每个障碍物最多16个点。轮廓点的最大数量是局部规划器的参数之一,【防盗标记–盒子君hzj】通过增加该数量,我们可以实现更精细的表示,从而可以更准确地避开障碍物
4)确定代价类型
(1)中心代价
中心代价每次roll-out都使用距该车道中心轨迹的绝对距离来计算,中心代价会限制车辆始终沿车道中心行驶,其他轨迹的渐变颜色代表代价
![]()
中心代价是对每条候选路径进行分级,中心路径的优先级是最高的,然后由中心路径向两边递减,这是为了在没有障碍物的情况下,让车辆保持在中心路径
(2)过渡代价
使用展开之间的归一化垂直距离以及当前选择的轨迹来计算过渡代价
过渡代价限制了车辆的roll-in,从而使转弯更平稳。
过渡代价是为了限制车辆不会频繁在候选路径之间切换,【防盗标记–盒子君hzj】这是为了确保车辆前进的平滑度
(3)碰撞代价
碰撞代价分两部分lateral_cost和longitudinal_cost来计算,以提高性能。lateral_cost候选路径到障碍物的横向水平距离,longitudinal_cost候选路径到障碍物的纵向水平距离
.
5)代价归一化处理
使用附加代价函数来评估每个轨迹,代价归一化处理计算三种不同的归一化代价度量,【防盗标记–盒子君hzj】包括代价,碰撞代价和过渡代价,避免评价函数中某一项代价占据过大的优势
.
.
6)通过代价函数计算代价,挑选出一条整体代价最低的一条局部路径
避开障碍的过程是展开轨迹中,先检测障碍物,再通过代价函数评估每一条展开的轨迹,最终选择出一条最优的轨迹
(4)局部路径规划器的跟踪路径
到这里得到无人车线控底盘的速度(speed)、角度(angular)指令
1.纯跟踪pure_persuit算法
原理和代码写在了我其他文章中…
.
2.模型预测控制MPC算法
原理和代码写在了我其他文章中…
.
(5)局部路径规划源码分析
后面补充
四、行为状态生成器【导航决策】
1、行为状态介绍
![]()
在实际开放道理场景下,自动驾驶要处理的场景非常繁杂:空旷的道路场景、与行人、障碍物共用道理的场景、空旷的十字路口、繁忙的十字路口、违反交通规则的行人/车辆、正常行驶的车辆/行人等等。场景虽然复杂,但都可以拆解为一系列简单行为(behavior)的组合,将这些简单的行为(behavior)组合起来,就可以完成复杂的驾驶行为
行为生成器使用预定义的交通规则和传感器数据充当协调器,【防盗标记–盒子君hzj】在局部路径规划过程中,根据道路的事件,触发行为生成器,当满足状态机的转换条件时,无人车进行路径的重新规划和速度的重新规划等,以响应道路事件。其中局部最优路径拼接起来大体时服从全局静态路径的
2、行为状态(也称任务、目标、状态)的定义
像交通规则一样,道路的事件本质上是确定的,【防盗标记–盒子君hzj】我们将对这些事件的响应称为行为,任务,目标,状态或情况,我们使用术语“行为状态”来表示所有这些事件响应
3、行为状态生成器的作用
处理诸如路径跟踪,目标跟踪,避障,紧急停车,在停车标志处停车和交通信号灯判断、改变车道、等待行人之类无人车的行为状态,重新规划无人车的相应行为
4、行为状态生成器步骤
(1)行为状态机的设计
1)背景
每个国家的交通规则有所不同。【防盗标记–盒子君hzj】因此需要随时添加或禁用特殊的交通规则。行为状态机的功能很难概括,因为它们的用法因机器人而异。OpenPlanner还提供基本的行为状态机功能,添加新状态与使用ROS一样容易。
2)交通状况和状态机的关系
OpenPlanner的行为状态生成模块充当系统的决策者。 它是一个有限状态机,其中每个状态代表一个交通状况
3)状态机的离散表示
通常使用状态机来表示任务,研究人员将连续驾驶行为状态转换为离散状态空间,然后使用搜索算法获得最佳任务序列,以在符号空间中达到目标条件
(2)状态机及状态转换条件
1)状态机转换条件
![]()
2)状态过渡参数
1)状态过度参数在每次迭代都要计算更新
2)计算控制状态过渡参数的方法
1、概率方法
从理论上讲,概率方法应该使过渡更平滑,【防盗标记–盒子君hzj】但是在广泛的应用程序中实现和维护它更慢,更复杂。
2、计时器和计数器方法【我们使用的】
解决此问题的一种方法是引入计时器和计数器
3)状态之间的转换由当前状态和状态过渡参数控制
(3)重新规划【结果】
行为生成器可以随时要求重新规划
(1)重新规划路径
(2)重新规划速度
.
.
.
五、总结
open_planner更适合用于无人驾驶(autoware)结构化和非结构化的场景
Open_planner也是使用增量式采样的方式进行路径探索和后端轨迹选择的
六、参考资料
OpenPlanner参考论文
Open Source Integrated Planner for Autonomous Navigation in Highly Dynamic Environments
OpenPlanner参考链接
https://blog.csdn.net/Travis_X/article/details/104607163
https://blog.csdn.net/Travis_X/article/details/115350840
视频展示
https://www.bilibili.com/video/BV1pL4y1Y78e?spm_id_from=333.999.0.0
https://www.bilibili.com/video/BV1if4y1V7Vw?spm_id_from=333.999.0.0
.
.
3.lexicographic_planner
![]()
一、lexicographic_planner介绍
open_planner更适合用于无人驾驶车道线场景,【防盗标记–盒子君hzj】lexicographic_planner更适合于农业的一垄一垄林场和仓库的场景,或者数原论文中阿无人船场景【属于replan局部规划的范畴,因为全局是给定路线的】
二、lexicographic_planner的整体流程
1.路径探索的步骤
(1)伪代码:
![]()
(2)步骤
(1)步骤一:当在规划过程的开始时收到全局路径G时,我们赋值全局路径globalPathMessage为探索路径并executePath
【planning中收到全局路径时的回调函数处理】
![]()
(2)步骤二:当机器人未完全执行全局路径G时,我们使用感知到的传感器数据S【局部代价地图】检查探索路径σ的可行性
(3)步骤三:(仅仅执行一次)判断给定的全局路径和所有障碍物是否相撞【即判断全局路径是否能被直接执行】,如果不能被直接执行且障碍物位于全局路径g上,【防盗标记–盒子君hzj】我们就以全局路径g为参考,生成候选的机器人规划的起点v(generation nodes V)
(4)步骤四:通过传感器以代价地图的方式更新障碍物的信息,【防盗标记--盒子君hzj】当机器人到达规划的起点v时,开始规划一条新的路径,具体replan的步骤如下:
![]()
【第一步】通过采样的(类似PRM)方法,生成一张有向的搜索图
这里和open_planner很像,但是open_planner不生成有向搜索图。lexicographic_planner会确定rollout的密度和数量,然后把候选的路径相互连接形成有向搜索的,生成rollout候选路径的采样方法是和open_planner一致的,只是lexicographic_planner多了把候选路径相互连接成有向图的过程
(类似于open_plannerde rollout阶段+PRM采样建立有向图的阶段)。【防盗标记–盒子君hzj】但注意的是,采样的过程不是用PRM均匀采样的方式,而是根据关键参数d(span),d(roll)和d(sensor)决定采样范围
采样函数buildAdjacencyMatrix()
建立一张PRM有向搜索图函数connectAdjacencyMatrix()
.
.
【第二步】lexicographic search在有向搜索图上进行路径搜索
(相当于PRM的有向图搜索阶段-搜索的方式使用Dijkstra,当然原理懂了图搜索的方法可以改)若搜索到一条可通行的路径,则输出可行路径。若搜索不到可通行的路径,则停下来并返回机器人当前的状态
![]()
(1)第0行:输入采样得到的有向搜索图、机器人的起始位置、终点位置
(2)第1行:根据有向图在队列Xqueue中填充图的节点
(3)第2~4行:为每个节点进行代价初始化,其中代价的初始值根据词袋优化代价的方法进行计算
(4)第5~24行:使用Dijkstra的方法进行路径探索,得到一条可通行的路径
.
.
2.路径优化的步骤
词典优化的方法将导航过程中需要解决的各种挑战建模成最小化代价,这样就将规划问题转化为多目标的优化问题。通过一种词典式高效的多目标搜索算法对所有目标进行分层排名快速解决多目标的规划问题,而无需对参数进行调整【防盗标记–盒子君hzj】
(1)代价函数的设计
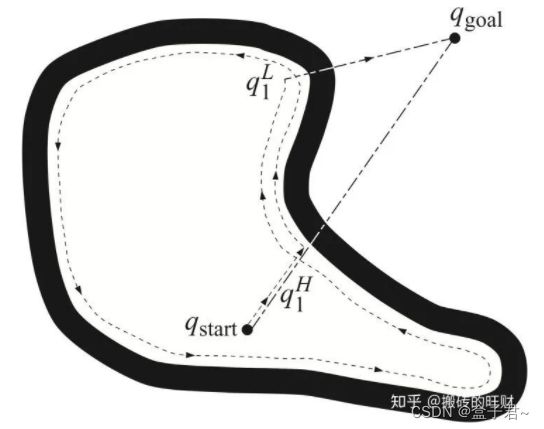
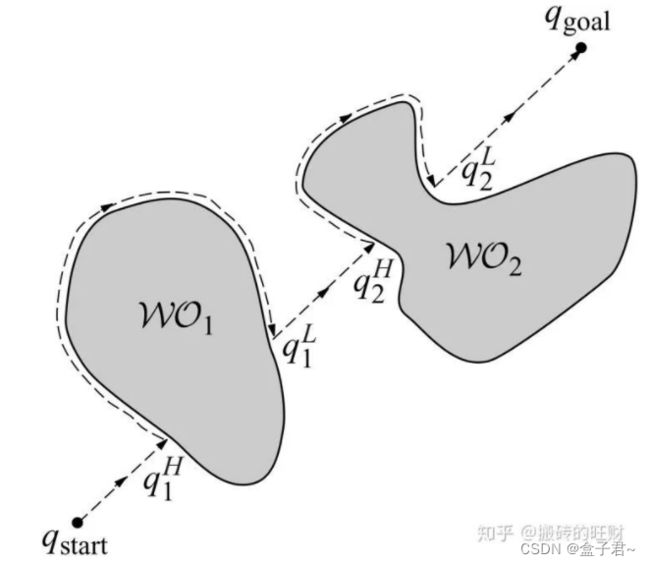
1、碰撞代价设计
(1)作用:保证机器人和其他车辆的安全
(2)碰撞代价函数的设计逻辑
![]()
希望在机器人与障碍物之间放置一块安全区域,机器人尽量避开该区域,以最大程度地减少其对其他船只的影响。创建该区域的另一种方法是单纯地对障碍区域进行膨胀。 但是,【防盗标记–盒子君hzj】如果障碍物之间离得很近,膨胀后也可能阻塞整个通行区域,即使是有一条可行的路径可以在它们之间通过
(3)沿着全局路径σ的风险碰撞计算公式
![]()
其中函数Risk函数评估单个机器人状态下的风险。假设R(x)定义为x与离x的最近障碍物之间的距离的倒数。如果R(x)大于风险阈值T hrisk,则会激活Risk()函数。例如,让T hrisk = 2,当机器人在障碍物的0.5 m以内时,Risk()会给出非零值。令让Thrisk = ∞时,在C(free)中任何一处Risk()都会返回0。
2、航向代价设计
(1)作用:惩罚了机器人规划的航迹和全局参考路径之间的航向差异,正确的打方向
(2)航向代价计算公式:
![]()
其中函数H(x)给出x与全局航线G上最接近x的路径段的航向之间的航向差。由于风浪干扰,将机器人的航向与G完美对齐几乎是不可能的。 为了避免全面的控制工作,我们定义了航向差异阈值Thhead。 【防盗标记–盒子君hzj】当误差H(x)大于T hhead时,Heading(x)返回一个非零值。 合并此代价可确保生成的路径在保持全局路径G航向的同时能相对平滑
3、行进距离代价设计
(1)作用:将行进距离定义为第三代价,严格来说这是正数。 这样可以确保不会像主要或次级代价那样频繁地发生
(2)行进代价计算公式:
![]()
(2)通过代价函数挑选最优路径【词袋优化的方法】
当两个或多个约束同时存在时会对这些约束进行分级惩罚的管理,【防盗标记–盒子君hzj】优先级高的约束承担惩罚的代价也就越高,当主要的惩罚代价没增加时,则会引入次要的代价或者次次要的代价
定义总代价函数为ck(σ), ck : Σ → R(+0),k∈ {1, 2, …, K}, K表示在多代价目标规划中子代价函数的数量,这些子代价函数适用于词典优化
![]()
3.lexicographic_planner与open_planner的对比
生成局部路径的思想大体和open_planner一致,但是主要不同在于:
(1)【路径收敛的策略 】open_planner在roll-out阶段生成的轨迹是不会收敛到给定路径G的,但是lexicographic_planner在roll-out阶段生成的轨迹会收敛到给定路径G
(2)open_planner和lexicographic_planner生成多条候选探索路径的方法是一样的,【防盗标记–盒子君hzj】只不过路径挑选的方法不一样,open_planner用代价优化的方法选择其中一条,lexicographic_planner用多条路径相互连接形成一张有向搜索图,用Dijkstra图搜索的方法探索出一条最优平滑路径
![]()
(3)【路径挑选的策略】open_planner在挑选路径的时候,使用了代价函数的方式对每一条候选路径进行评价挑选(因为open_planner没有建立搜索图),但是lexicographic_planner通过open_planner生成的多条候选路径的基础上,把每条候选路径上的邻接节点相连接,建立了有向搜索图的基础上使用了A*(Dijkstra)的方法唯一进行路径的探索【有向图建立+Dijkstra=PRM的思想】
![]()
(4)【代价函数用的方向策略】open_planner的代价函数用于评价挑选候选路径,lexicographic_planner的代价函数用于初始化采样节点的代价,建立带有代价的有向搜索图
4.lexicographic_planner的效果图
![]()
三、lexicographic_planner源码解读
1.输入输出
输入规划器将机器人的当前状态xc,全局参考路径G和感知传感器数据S(局部地图、定位)
输出为n条平滑轨迹,从车辆中心线一直避障延伸,最后又收敛回到车辆中心线
2.需要调试的参数
在工程的.yaml文件
其规划范围由关键参数d(span),d(roll)和d(sensor)决定
d(span)是采样状态和全局路径G之间的最大距离,实际上,【防盗标记–盒子君hzj】在障碍物覆盖的区域d(roll)设置的值比传感器的范围要大
d(roll)是roll-out和oll-in部分之间的总距离
d(sensor)是传感器能探测的距离
3.lexicographc_planner的运行过程
lexicographc_planner本来是在给定的全局路径下执行巡航的,没有检查到障碍物就继续执行跟踪全局路径的功能,检查在全局路径上到有障碍物才启动replan,planning先在全局路径上截取一小段局部路径(由d(sensor)参数决定),从而确定planing的起点和终点,然后就按着lexicographic的plan计划来
(1)【障碍物在全局路径上,启动重规划】obstacles on path,replanning
(2)【撞到障碍物或者规划失败,停下来】planning fail,no path found,stay
(3)停下来后需要重新给定新的目标点(起点就是机器人现在位置)
4.lexicographic_planner源码解读
先写下框架,到吗后续补充~
(1)_cloudRegister(处理三维点云,转换成全局坐标)
功能:负责接收点云信息的处理,包括坐标转换、下采样、滤波等等(大多数时用PCL库实现的),最后把处理后的点云数据发布出来
(2)_obstacleServer(生成局部代价地图)
功能:把三维点云地图转换成为二维的栅格地图(并带有代价值和膨胀层)【点云接收回调函数中处理】
(3)_pathServer(全局路径加载)
功能:创建原始全局路径(点)发布器的与平滑全局路径发布器,同时创建一个定时器,一秒执行一次updatePath()函数更新全局路径,全局路径根据机器人位置不断在两个半圆路径上进行切换,并发布平滑后的全局路径
(4)_pathPlanning(局部规划)
1)订阅全局参考路径回调函数【void pathHandler(const nav_msgs::Path::ConstPtr& pathMsg)】
功能:确定原始全局路径作为搜索路径,进行openPlannerRollOut的过程,生成多条候选路径
2)订阅局部代价地图回调函数【void mapHandler(const nav_msgs::OccupancyGrid::ConstPtr& mapMsg)】
功能:把局部代价地图转存到内存变量中occupancyMap2D
3)定时更新路径(与上面的原理一致)【void updatePath(const ros::TimerEvent& event)】
(1)通过采样,建立邻接矩阵【buildAdjacencyMatrix ();】
(2)通过连接邻接矩阵,建立一张PRM有向搜索图【connectAdjacencyMatrix (); 】
(3)在有向搜索图(邻接矩阵)进行搜索,得到一条新的局部路径【searchAdjacencyMatrix ();】
(4)可视化【visualization (); 】
四、总结
1.优点
(1)lexicographic_planning的横向搜索范围可以改【像open_planner一样改】
(2)lexicographic_planning在规划中间的区域,效果是和理想的
2.缺点
(1)lexicographic_planning在规划最后收敛搜索的时候若是遇到了障碍物,很容易就会规划失败
(2)【局部地图问题】使用二维的激光雷达,【防盗标记–盒子君hzj】只能扫出一个平面的点云信息,激光雷达过高或者过低都没办法得到有效的局部代价地图
(3)lexicographic_planner算法本身时没有什么问题的,但是不足的地方就是用了move_base(DWA_planner),导致局部避障的时候会运行两个局部规划器,先是lexicographic_planner,后面差速车执行的靠DWA_planner,最后执行的路径是两个规划器的结果,相互影响,难以调试
五、参考资料
1、论文
A Receding Horizon Multi-Objective Plannerfor Autonomous Surface Vehicles in Urban Waterways
https://arxiv.org/abs/2007.08362
2、代码
https://github.com/TixiaoShan/lexicographic_planning
3、博客参考
https://blog.csdn.net/Travis_X/article/details/115485931
4、视频参考
https://www.bilibili.com/video/BV18V411n7Pw?spm_id_from=333.999.0.0
4.Teb_planner
一、Time Elastic Band算法算法核心思想
Time Elastic Band算法可以在给定路径的基础上对轨迹进行优化(局部规划),没有了replan的路径探索部分,仅仅有轨迹优化部分使轨迹变形
teb算法将避障硬约束转换为软约束,【防盗标记–盒子君hzj】将给定的路径视为受内外力影响的弹性橡皮筋,使其变形,而内外力相互平衡,使路径收缩,同时与障碍物保持一定的距离,其中内外力就是对机器人运动的所有约束。而对于time eletic band,则在给定路径中间插入N个控制橡皮筋形状的控制点(机器人姿态),在点与点之间定义运动时间Time,即为Time Elastic Band算法。
Time Elastic Band算法把路径规划问题描述为一个多约束目标优化问题,即对最小化轨迹执行时间、与障碍物保持一定距离并遵守运动动力学约束等目标进行优化。因为优化的大多数目标都是局部的,【防盗标记–盒子君hzj】只与机器人的某几个连续的状态有关,所以该优化问题为对稀疏模型的优化。通过求解稀疏模型多目标优化问题,可以有效获得机器人的最佳运动轨迹
二、Time Elastic Band算法的约束条件
从给定全局路径中得到一系列带时间信息的离散位姿(pose),【防盗标记–盒子君hzj】通过图优化的方法将这些离散位姿组成满足时间最短、距离最短和远离障碍物等目标的轨迹,同时满足机器人运动动力学的约束。需要注意的是,优化得到的轨迹并不一定满足所有约束,即给定的约束条件实际上都是软约束条件
1.最小化轨迹时间约束条件
约束公式待补充
2.与障碍物保持距离约束条件
约束公式待补充
3.对轨迹与障碍物的距离约束条件
约束公式待补充
4.跟随全局路径约束条件
作用:一定要经过全局路径某一个点
约束公式待补充
5.跟随全局路径约束条件
作用:线速度,角速度的约束
约束公式待补充
三、Time Elastic Band算法多约束的实现
1.时变弹性带的轨迹模型+footprint机器人模型类
2.配置TEB的参数类
3.设计约束优化类
4.g2o优化时变弹性带的轨迹类【TebOptimalPlanner】
5.局部规划器对外调用的接口类【PlannerInterface】
6.将teb_localplanner插件化,使之能被集成到ROS导航包的类【TebLocalPlannerROS】
四、Time Elastic Band算法流程(伪代码)

求解稀疏模型多目标优化问题的方法
teb_localplanner是以优化的方法进行轨迹优化的,使用的优化库是g2o,优化的目的是寻找代价最小的轨迹解决方案。
可通过构建超图(hyper-graph),【防盗标记–盒子君hzj】使用g2o(通用图优化)框架中关于大规模稀疏矩阵的优化算法来求解。机器人状态和时间间隔作为nodes,目标函数和约束函数作为edges,各nodes由edges连接构成hyper-graph。在该hyper-graph中,每个约束为一条edge,且每条edge允许连接的nodes的数目不受限制
五、Time Elastic Band算法部署
(1)Time Elastic Band算法的安装方法
(1)二进制安装
指令
sudo apt-get install ros-kinetic-teb-local-planner
sudo apt-get install ros-kinetic-teb-local-planner-tutorials
优缺点
快速安装部署,但是没法修改程序,因为安装的是编译后的二进制文件
(2)源码安装
源码网址
https://github.com/rst-tu-dortmund/teb_local_planner
教程参考【还有测试用例】
https://blog.csdn.net/shanpenghui/article/details/89091064
.
.
.
(2)Time Elastic Band算法的调参使用
teb_local_planner提供了许多参数和权重的配置接口,在不同的约束条件下指定优化目标,设定合理的参数值
1、Homotopy Class Planner参数
使用多条轨迹的teb算法:the homotopy class planning algorithm会尝试沿着障碍物构成的拓扑地图,【防盗标记–盒子君hzj】寻找多条轨迹。避免陷入极值
teb_local_planner中的Homotopy Class Planner,用户可以将enable_multithreading参数设置为True来开启同时规划多条路径,在某些极端条件下,同时规划多条路径并选取最优轨迹得到的轨迹更符合全局最优,也更合理。当然,同时规划多条路径也将消耗更多的机器性能。在实际应用过程中,用户应当根据具体情况合理取舍。
enable_homotopy_class_planning: True
enable_multithreading: True
max_number_classes: 4
selection_cost_hysteresis: 1.0
selection_prefer_initial_plan: 0.9
selection_obst_cost_scale: 100.0
selection_alternative_time_cost: False
roadmap_graph_no_samples: 15 # Homotopy Class Planner
roadmap_graph_area_width: 5
roadmap_graph_area_length_scale: 1.0
h_signature_prescaler: 0.5
h_signature_threshold: 0.1
obstacle_heading_threshold: 0.45
switching_blocking_period: 0.0
viapoints_all_candidates: True
delete_detours_backwards: True
max_ratio_detours_duration_best_duration: 3.0
visualize_hc_graph: False
visualize_with_time_as_z_axis_scale: False
2、 Trajectory参数
有效地跟随全局路径约束(一定要经过全局路径某一个点)的调参接口

(1)dt_ref:参考轨迹的离散间隔
(2)obstacle_poses_affected: 因为障碍物而受到影响的poses数量(基于距离障碍物最近的pose,向两边扩展的点数)只有被affected的pose会被选中拿去做优化
(3)global_plan_viapoint_sep参数以及相应的权重:当global_plan_viapoint_sep的值比较小时,从全局路径中选取的viapoint比较密集,最优轨迹对全局路径的跟随效果比较好;当global_plan_viapoint_sep的值比较大时,【防盗标记–盒子君hzj】从全局路径中选取的viapoint比较稀疏,最优轨迹对全局路径的跟随效果比较差,但此时的最优轨迹可能更加平滑
(4)viapoint可以理解为通过点,即要求teb_local_planner规划出的轨迹必须通过某个点
teb_autosize: True
dt_ref: 0.3
dt_hysteresis: 0.1
max_samples: 500
global_plan_overwrite_orientation: True
allow_init_with_backwards_motion: False
max_global_plan_lookahead_dist: 3.0
global_plan_viapoint_sep: -1
global_plan_prune_distance: 1
exact_arc_length: False
feasibility_check_no_poses: 5
publish_feedback: False
3、Robot参数
遵循运动学动力学约束(线速度,角速度的约束)的调参接口
max_vel_x: 0.4
max_vel_x_backwards: 0.2
max_vel_y: 0.0
max_vel_theta: 0.3
acc_lim_x: 0.5
acc_lim_theta: 0.5
min_turning_radius: 0.0 # diff-drive robot (can turn on place!)
footprint_model:
type: "point"
4、Obstacles参数
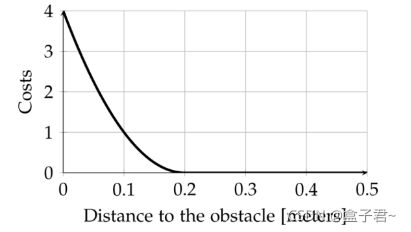
min_obstacle_dist和inflation_dist两个参数的值会导致teb_local_planner规划出不同的轨迹。min_obstacle_dist可以视为比inflation_dist更为严格的约束条件,只有当inflation_dist的值大于min_obstacle_dist时,inflation_dist才会影响teb_local_planner规划出的轨迹
min_obstacle_dist: 0.25 # 最小避障距离
weight_obstacle: 1 #避障在整个优化函数中的权重
inflation_dist: 0.6
include_costmap_obstacles: True
costmap_obstacles_behind_robot_dist: 1.5
obstacle_poses_affected: 15
dynamic_obstacle_inflation_dist: 0.6
include_dynamic_obstacles: True
costmap_converter_plugin: ""
costmap_converter_spin_thread: True
costmap_converter_rate: 5
5、 GoalTolerance参数
xy_goal_tolerance: 0.2
yaw_goal_tolerance: 0.1
free_goal_vel: False
complete_global_plan: True
6、Optimization参数
no_inner_iterations: 5
no_outer_iterations: 4
optimization_activate: True
optimization_verbose: False
penalty_epsilon: 0.1
obstacle_cost_exponent: 4
weight_max_vel_x: 2
weight_max_vel_theta: 1
weight_acc_lim_x: 1
weight_acc_lim_theta: 1
weight_kinematics_nh: 1000
weight_kinematics_forward_drive: 1
weight_kinematics_turning_radius: 1
weight_optimaltime: 1 # must be > 0
weight_shortest_path: 0
weight_obstacle: 100
weight_inflation: 0.2
weight_dynamic_obstacle: 10
weight_dynamic_obstacle_inflation: 0.2
weight_viapoint: 1
weight_adapt_factor: 2
7、Recovery参数
shrink_horizon_backup: True
shrink_horizon_min_duration: 10
oscillation_recovery: True
oscillation_v_eps: 0.1
oscillation_omega_eps: 0.1
oscillation_recovery_min_duration: 10
oscillation_filter_duration: 10
六、Time Elastic Band算法的优缺点
(1)优点
(1)可以满足多种约束,如时间最短、距离最短、远离障碍、运动学动力学约束【防盗标记–盒子君hzj】
(2)Teb可以实现静态/动态障碍物、通过给定点、最小转向半径等多种约束条件下的时间最优轨迹规划,具备这样优秀特性的规划方法实在不多,更难能可贵的是它还给出了详细的例子和规范的代码
(3)车底盘支持差速模型给和阿克曼模型【防盗标记–盒子君hzj】
(2)缺点
(1)Time Elastic Band算法的大多数约束都是软约束条件,在真正场景下不完全可控
(2)通用性强,因此要针对一个特定的场景【防盗标记–盒子君hzj】,需要大量调节参数,若参数和权重设置不合理或者环境过于苛刻,都有可能导致Time Elastic Band算法规划失败,出现非常奇怪的轨迹。
(3) 控制量不平滑,尤其是前轮的转角上蹿下跳
(4) 解的质量不稳定,因为采用了数值优化的方法计算轨迹,所以对初值敏感。同样的起点和终点,不同的初值会得到不同的轨迹。轨迹有时候比较好,【防盗标记–盒子君hzj】但你不知道什么时候质量会比较差(看起来很怪异,各种倒车)
七、总结
由于ROS中的局部路径规划器比较老了,所以我推荐大家使用比较新的局部路径规划器teb_local_planner。teb_local_planner是基于弹性时间带碰撞约束的算法,算法将动态障碍物、运行时效、路径平滑性等约束做综合考虑,在复杂环境下有更优秀的表现
利用teb算法实现实时的路径规划,【防盗标记–盒子君hzj】是当前较为稳定与常用的局部路径规划器,扩展性较强,并且支持阿克曼转向的路径规划,此插件时塔克创新的机器人所使用的局部路径规划插件
参考资料
http://wiki.ros.org/teb_local_planner/Tutorials/Setup%20and%20test%20Optimization
(1)链接参考
https://zhuanlan.zhihu.com/p/391093849
https://www.guyuehome.com/33764
http://wiki.ros.org/teb_local_planner_tutorials
https://www.pianshen.com/article/3698267335/
https://www.ncnynl.com/archives/201809/2611.html
https://blog.csdn.net/qq_41986495/article/details/85060538
https://blog.csdn.net/allenhsu6/article/details/113523546
http://wiki.ros.org/teb_local_planner/
(2)论文参考
(1)Time Elastic Band算法以及使用稀疏模型进行优化方向
[1].C. Rösmann, W. Feiten, T. Wösch, F. Hoffmann and T. Bertram: Trajectory modification considering dynamic constraints of autonomous robots. Proc. 7th German Conference on Robotics, Germany, Munich, 2012, pp 74–79.
[2].C. Rösmann, W. Feiten, T. Wösch, F. Hoffmann and T. Bertram: Efficient trajectory optimization using a sparse model. Proc. IEEE European Conference on Mobile Robots, Spain, Barcelona, 2013, pp. 138–143.
(2)同时规划多条轨迹,并选取出当前的全局最优轨迹方向
[1].C. Rösmann, F. Hoffmann and T. Bertram: Integrated online trajectory planning and optimization in distinctive topologies, Robotics and Autonomous Systems, Vol. 88, 2017, pp. 142–153.
[2].C. Rösmann, F. Hoffmann and T. Bertram: Planning of Multiple Robot Trajectories in Distinctive Topologies, Proc. IEEE European Conference on Mobile Robots, UK, Lincoln, Sept. 2015.
(3)类汽车机器人的轨迹优化方向
[1].C. Rösmann, F. Hoffmann and T. Bertram: Kinodynamic Trajectory Optimization and Control for Car-Like Robots, IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Vancouver, BC, Canada, Sept. 2017
(3)视频展示
[https://www.bilibili.com/video/BV1FM4y157qd?spm_id_from=333.999.0.0](https://www.bilibili.com/video/BV1F
.
.
二、控制的方法
1.应激式BUG局部避障算法
(1)应激式BUG算法原理
BUG算法是一种完全应激的机器人避障算法。其算法原理类似昆虫爬行的运动决策策略。在未遇到障碍物时,沿直线向目标运动;在遇到障碍物后,沿着障碍物边界绕行,【防盗标记–盒子君hzj】并利用一定的判断准则离开障碍物继续直行.
BUG算法是一种完全应激的机器人避障算法。其算法原理类似昆虫爬行的运动决策策略。在未遇到障碍物时,沿直线向目标运动;在遇到障碍物后,沿着障碍物边界绕行,并利用一定的判断准则离开障碍物继续直行。这种应激式的算法计算简便,不需要获知全局地图和障碍物形状,具备完备性。但是其生成的路径平滑性不够好,对机器人的各种微分约束适应性比较差。
.
(2)应激式BUG算法优点
应激式的算法计算简便,不需要获知全局地图和障碍物形状,具备完备性
.
(3)应激式BUG算法缺点
其生成的路径平滑性不够好,【防盗标记–盒子君hzj】对机器人的各种微分约束适应性比较差
.
(4) BUG1算法
该算法的基本思想是在没有障碍物时,沿着直线向目标运动可以得到最短的路线。当传感器检测到障碍物时,机器人绕行障碍物直到能够继续沿直线项目标运动。BUG1算法实现了最基本的向目标直行和绕行障碍物的思想。
BUG1算法运动规划示意图
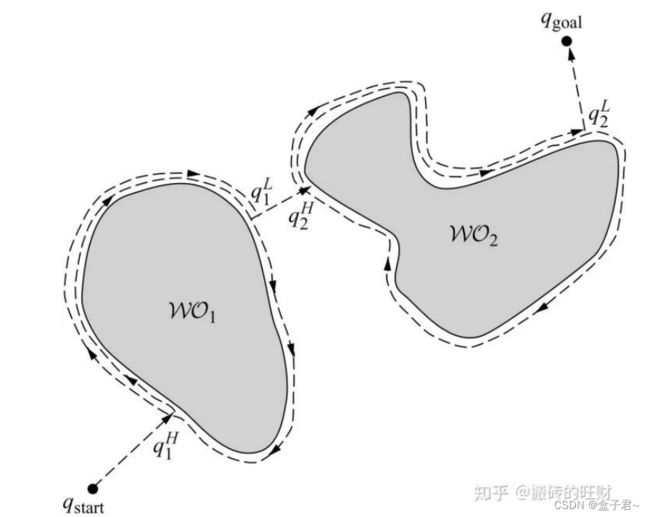
假设机器人能够计算两点之间的距离,并且不考虑机器人的定位误差。初始位置和目标位置分别用q (start) 和 q(goal)表示;机器人在i时刻的位置表示为xi;L表示连接机器人位置xi和目标点的直线。初始时,q (start)=xi。若没有探测到障碍物,那么机器人就沿着L向目标直行,直到到达目标点或者遇到障碍物。当遇到障碍物时,记下当前位置qH(i) 。然后机器人环绕障碍物直到又一次到达qH(i) ,找到环绕路线上距离目标最近的点qL(i),并沿着障碍物边界移动到该点。随后,直线L更新,机器人继续沿直线向目标运动。如果沿这条直线运动时还会遇到该障碍物,那么机器人不能到达目标点。否则算法不断循环直到机器人到达目标点或者规划器认为机器人无法到达目标点。
(5)BUG2算法
BUG2算法也有两种运动:朝向目标的直行和沿边界绕行。与BUG1算法不同的是,BUG2算法中的直线 L是连接初始点和目标点的直线,在计算过程中保持不变。当机器人在点遇到障碍物时,机器人开始绕行障碍物,如果机器人在绕行过程中在距离目标更近的点再次遇到直线L,那么就停止绕行,继续沿着直线 L向目标直行。如此循环,直到机器人到达目标点 图片 。如果机器人在绕行过程中未遇到直线 L 上与目标更近的 qL(i) 点而回到了 qH(i)点,那么得出结论,机器人不能到达目标。
BUG2算法中认为机器人无法到达目标点的情况示意图
![]()
(6)BUG1和BUG2算法对比
BUG1和BUG2算法提供了搜索问题的两种基本方法:比较保守的BUG1算法进行详细的搜索来获得最佳的离开点。这需要机器人环绕整个障碍物的边界。而BUG2算法使用一种投机的方法。机器人不环绕完整的障碍物,而选择第一个可用的点作为离开点。对于一般的环境,BUG2算法的效率更高;而对于复杂形状的障碍物,保守的BUG1算法性能更优。
.
(7)逻辑方形超声波绕障
割草机方案~
.
(8)总结
更粗暴,算法理论更地一级的时方形绕障碍–匹配适合场景实现效果就行
感知传感器用超声波雷达、毫米波雷达、激光雷达 、视觉等等距离传感器
.
(9)参考资料
https://mp.weixin.qq.com/s/0q6t_ibrKjBvjcox6wFK6g
2.滑动窗口DWA_planner
(1)DWA_planner算法基本原理
1.DWA_planner图例
![]()
在每一个控制周期搜索最佳的局部路径规划。首先局部规划器会生成一些候选轨迹。其次在检测生成的轨迹是否会与障碍物碰撞。如果没有,规划器就会评价且比较选择出最好的轨迹
简单来说,TrajectorySampleGenerator产生一系列轨迹,然后TrajectoryCostFunction遍历轨迹打分,TrajectorySearch找到最好的轨迹拿来给小车导航;由于小车不是一个质点,【防盗标记–盒子君hzj】worldModel会检查小车有没有碰到障碍物
DWA整体流程和base_local_planner相似,只是重新写了computeVelocityCommands的实现
2.DWA_planner输入输出
(1)输入如下
全局路径global_plan ( nav_msgs/Path)
局部代价地图Costmap2D
机器人的状态(当前速度)odom ( nav_msgs/Odometry)
(2)输出差速机器人底盘的twist指令
(规划和控制集成一体–基于控制状态采样)
3.DWA算法过程(直观理解)
步骤一:在机器人控制空间进行速度控制量离散采样(dx,dy,theta)【防盗标记–盒子君hzj】
步骤二:对每一个采样速度执行前向模拟,看看使用该采样速度(v,w)移动一小段时间后会发生什么
步骤三:评价前向模拟中每个轨迹,评价准则如: 靠近障碍物,靠近目标,贴近全局路径和速度;丢弃非法轨迹(如哪些靠近障碍物的轨迹)
步骤四:挑出得分最高的模拟轨迹对应的速度控制量并发送相应速度给移动底座
重复上面步骤
4.DWA_planner源码的主要接口及原理
(1)initialize()初始化
(2)setPlan()负责获取全局路径
DWAPlannerROS::setPlan获取后,转发给DWAPlanner::setPlan,恢复振荡标志位再转发给LocalPlannerUtil::setPlan,这样层层叠叠的调用很有层次感,【防盗标记–盒子君hzj】这样每当产生一个新的全局路径都第一时间提供给全局——局部转化以及剪裁功能使用
(3)computeVelocityCommands()计算本次控制速度
1、costmap_ros_->getRobotPose(current_pose_)先确定小车当前在全局中位置,负责将小车自身的位姿用tf转化为全局位姿
2、LocalPlannerUtil::getLocalPlan根据小车当前位置裁剪前方一小段路径,将全局路径转化到局部路径,位于base_local_planner包local_planner_util.cpp中
3、DWAPlanner::findBestPath会查找最优局部轨迹,首先调用SimpleTrajectoryGenerator::initialise进行速度采样,然后利用SimpleScoredSamplingPlanner::findBestTrajectory根据速度采样空间进行轨迹产生、打分、筛选,从而得到最优局部轨迹
4、DWAPlanner::updatePlanAndLocalCosts函数调用了MapGridCostFunction即根据栅格地图产生一系列打分项
5、调用LatchedStopRotateController::isPositionReached判断是否到终点了,只是通过判断终点和当前位置的算术距离
6、若到终点了,调用LatchedStopRotateController::computeVelocityCommandsStopRotate函数,使小车旋转至最终姿态;否则继续调用dwaComputeVelocityCommands函数计算下发速度
(4)bool isGoalReached()判断是否达到目标点
(2)总结
1.算法部署方面
(1)DWA_planning是move_base默认的局部规划器
(2)该算法思想比较简单,且ROS已经封装成以一个功能包,【防盗标记–盒子君hzj】比较容易部署与移植
(3)将路径规划器和机器人车底盘控制器集成在一起,其中车底盘模型默认是差速车底盘
(4)算法地图支持,DWA_planning非常依赖于局部地图,特别是局部地图的更新频率和膨胀区的设置
(5)算法定位支持,DWA_planning根本不需要定位信息,仅仅通过odom里程计拿到车辆的速度就行,所以自然都不用对odom里程计进行积分产生漂移了,适合部署,仿真拿定位还要多一步搞到定位信息了
2.算法思想
算法优化的代价函数统筹好【防盗标记–盒子君hzj】追踪全局路径、朝向代价、速度代价、障碍物代价几个评价标准,利用评价函数挑选模拟采样的最优的前向轨迹,进而根据最优的前向模拟轨迹反推确定发送给底座的速度(dx,dy,dtheta)
但没有用到图搜索思想、状态采样思想、也没有用到动力学思想,运动纯靠控制状态采样的,偏向短期的局部应激规划,整体运动效果不太好,先给一个速度看看效果,移动后再通过动态窗口看看下一步应该给什么速度,见步走步,像一个玩具的移动机器人一样,没有远见性,运动可能时一卡一卡的,【防盗标记–盒子君hzj】因为没有考虑轨迹的平滑性和动力学【在障碍物时移动的情况下,效果更差】
【基于控制量采样和状态量采样的异同】DWA_planning的采样方式是基于控制量进行采样(通过odom获得底盘速度就行),所以输出的是速度控制指令,state_lattice_planner的采样方式是基于状态量进行采样(需要直到全局定位),所以输出的是一条带有状态的轨迹
3.算法缺点
DWA_planning到达目标点后,才通过旋转达到对准朝向,【防盗标记–盒子君hzj】规划的时候不考虑车底盘的朝向的,到了目标点才旋转摆正车身,真正机器人允不允许这么做
(3)参考资料
参考视频
https://www.bilibili.com/video/BV1MQ4y1179T?spm_id_from=333.999.0.0
DWA_planner局部路径规划算法论文阅读
https://www.cnblogs.com/dlutjwh/p/11158233.html
DWA_planner源码github地址
https://github.com/amslabtech/dwa_planner
DWA_planner源码分析
https://www.cnblogs.com/sakabatou/p/8297479.html
.
.
3.base_local_planner
(1)(ROS)base_local_planner介绍
base_local_planner 提供用Dynamic Window and Trajectory Rollout approaches来做局部规划控制,与base_local_planner相比,专用的DWA局部规划插件具有更加整洁,更加易用的界面,机器人更容易理解,【防盗标记–盒子君hzj】由更灵活的y轴变量
(2)Trajectory Rollout基本算法原理
DWA与Trajectory Rollout的区别主要是在机器人的控制空间采样差异。Trajectory Rollout采样点来源于整个前向模拟阶段所有可用速度集合,而DWA采样点仅仅来源于一个模拟步骤中的可用速度集合。【防盗标记–盒子君hzj】这意味着相比之下DWA是一种更加有效算法。因为其使用了更小采样空间;然而对于低加速度的机器人来说可能Trajectory Rollout更好,因为DWA不能对常加速度做前向模拟。
在实践中,我们经过多次实验发现Trajectory Rollout、DWA方法性能基本相当,【防盗标记–盒子君hzj】这样的话我们推荐使用效率更高的DWA算法
(3)(ROS)base_local_planne运行流程
![]()
在move base中进行TrajectoryPlannerROS这里更封装过的类进行初始化了。每次有goal发布的时候,都会去调用executeCb,executeCb会去调用executeCycle
进行local plan,发布cmd_vel的topic,根据小车处于的状态,【防盗标记–盒子君hzj】进行相应的实现(会进行plan,control,clear obstacle)
整一个逻辑顺序就是computeVelocityCommands->findBestTrajectory --> createTrajectories --> generateTrajectory。最终,选择分数最低的轨迹,发布出去。这便是整个局部规划器的实现思路和逻辑
(4)(ROS)base_local_planner核心函数
(1)initialize()【初始化局部规划器】
实现的功能及流程

(2)setPlan()
【只是规划标志位设定而已】
(3)isGoalReached()
【检查局部规划师是否达到了目标姿势】
(4)computeVelocityCommands()
实现的功能及流程
【计算机器人实际运行的速度和位置控制指令,发布局部路径规划,是base_local_planner的核心】

其他都是自己的定义的被调函数了
(5)findBestPath()路径探索的核心原理
base_local_planner基础代码已经被扩展成很多个接口
(0)给定栅格地图Grid Map和全局路径
为了有效地评价轨迹,必须依赖地图栅格,每个控制周期,【防盗标记–盒子君hzj】都会在机器人周围创建局部栅格地图(大小为局部costmap区域),并且全局路径会被映射到这个区域上。这时候的局部代价地图既有静态信息,又有动态信息。同时,有一定栅格将被标记为到全局路径点距离为0
(1)TrajectorySampleGenerator接口
功能:【产生一系列轨迹】

该接口描述了一种产生一系列局部路径的发生器,每调用一次nextTrajectory()就会返回一个新的轨迹。其中,SimpleTrajectoryGenerator类可以使用trajectory rollout或DWA原理来生成根据加速度的限制产生一系列轨迹(轨迹就是速度跟点的集合,在trajectory.h中定义),以供后面打分挑选
.
.
.
(2)TrajectoryCostFunction接口
功能:【建立四个代价函数,遍历轨迹进行打分】
这个接口包含了最重要的函数scoreTrajectory(),【防盗标记–盒子君hzj】 该函数输入轨迹后会输出轨迹评价分数。如果输出负分数意味着轨迹无效;输出分数为正值,对于cost函数来说值越小越好。每个cost函数有一个比例因子,与其它cost函数比较时候,通过调节比例因子,cost函数影响可以被改变。
具体的子代价函数如下:

(1)TrajectoryCostFunction,这个接口主要规定了一个scoreTrajectory函数,也就是走过一个轨迹需要付出的代价,在wiki上可以看到对4种代价的详细介绍;
(2)MapGridCostFunction用来评估局部规划的轨迹离全局规划的轨迹的距离,也可以用来评估到目标的距离
(3)ObstacleCostFunction就是计算小车在costmap上行走的代价【防盗标记–盒子君hzj】,看看是否撞到障碍。其中ObstacleCostFunction用到了worldModel接口来检测底座是不是撞到障碍物,从初始化函数可以看出来,ObstacleCostFunction选用了CostmapModel作为具体实现
(4)oscillationcostFunction判断小车是不是老是震动
(5)preferForwardCostFunction判断小车会不会倒着走
.
.
.
(3)SimpleScoredSamplingPlanner接口
功能:【这是一个循环实现–ScoredSamplingPlanner把一系列(4个)costFunction子代价评价函数打分加起来,选代价最低的轨迹,最后TrajectorySearch找到最优的局部路径】

这是轨迹搜索的一种简单实现,利用了TrajectorySampleGenerator产生的轨迹和一系列TrajectoryCostFunction。 它会一直调用nextTrajectory()直到发生器停止生成轨迹。对于每一个生成的轨迹,【防盗标记–盒子君hzj】将会把列表中的cost函数都循环调用,并把cost函数返回的正值,负值丢弃。 最佳轨迹就是cost函数加权求和后最好的的那条轨迹。
.
.
.
(4)局部规划器提供支持的一些类
(1)LocalPlannerUtil
管理当前的全局规划,当前的运动约束,以及当前的cost地图(感知障碍物的局部cost地图)
(2)OdometryHelperRos
提供odometry信息
(3)atchedStopRotateController
当机器人足够靠近目标时可以迅速启用改控制器
(4)FootprintHelper
打印机器人运功的轨迹出来
(5)worldModel类会给检查小车有没有碰到障碍物提供支持
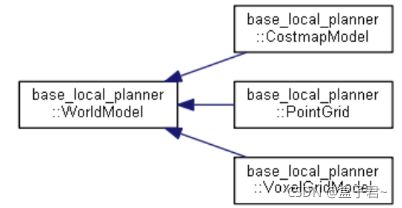
worldModel:检查给定位置和方向上的足迹在世界上的合法性
(5)TrajectoryPlannerROS接口
【这个是遵循navcore接口的】
base_local_planner::TrajectoryPlannerROS是对base_local_planner::TrajectoryPlanner的ROS封装。【防盗标记–盒子君hzj】它在初始化时确定的ROS命名空间内运行,该接口继承了nav_core包的nav_core::BaseLocalPlanner接口。
三、曲线的方法
1.double S直线速度规划
路径-速度解耦规划
路径-速度解耦规划将轨迹规划分为两步:路径规划和速度规划。
路径规划:生成候选曲线,这是车辆可行驶的路径,使用代价函数对每条路径进行评估,该函数包括平滑度、安全性、与车道中心的偏离等等,按代价对路径进行排名,并选择代价最低的路径。
速度规划:确定沿这条路径行进的速度,可以使用优化功能为路径选择受到各种限制约束的良好速度曲线
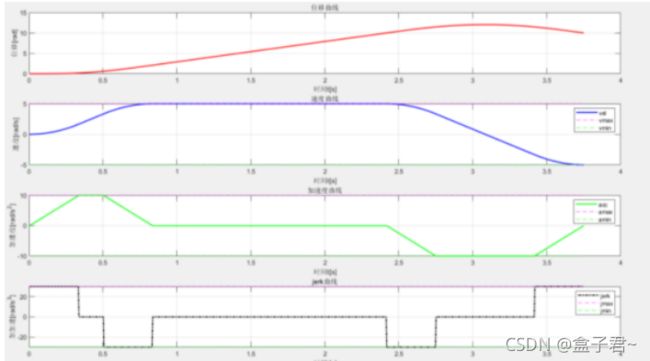
(1)Double S曲线速度规划介绍
1.介绍
Double S规划也叫S形曲线规划,S轨迹也称作七段轨迹曲线,因此主要由七段函数构成。,Point to Point的直线速度规划
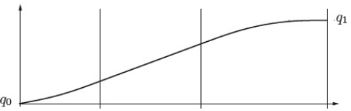
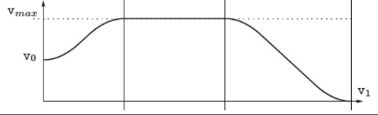
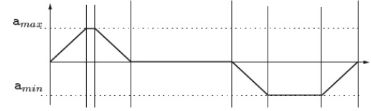
.
2.图例
位置曲线
速度曲线
加速度曲线
加加速度曲线
标记
q0:起点
q1:终点
v0:初始速度
v1:终点速度
a0:初始加速度
a1:终点加速度
j0:初始加加速度
j1:终止加加速度
t0:开始时间【防盗标记–盒子君hzj】
t1:终止时间
T:总时间
Vmax:最大速度
amax:最大加速度
jmax:最大加加速度
.
.
3.适合场景
直线段的梯形加减速的速度规划
输出控制的速度、加速度、加加速度的指令(当然仅仅是输出其中一个也行,能控住其中一个,其他两个量也控制住了,主要是看机器人的底盘接收什么信号)【防盗标记–盒子君hzj】
.
4.应用对象
机械臂常用的轨迹曲线主要是S曲线
路径规划的速度规划【防盗标记–盒子君hzj】
.
(2)double S曲线原理及步骤
1.系统参数定义
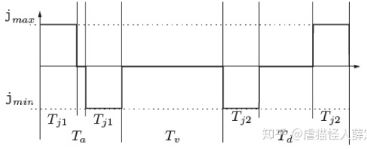
Tj1:在加速段中满足(jmax或者jmin)所需的时间周期时间
Tj2:在减速段中满足(jmax或者jmin)所需的时间周期时间
Ta:加速段周期
Td:减速段周期【防盗标记–盒子君hzj】
Tv:匀速时间
T:整条曲线的总时间
.
.
2.给定曲线的系统参数(假设参数)

通过给定最大速度、最大加速度、最大加加速度,通过合理改变曲线的速度、加速度、加加速度使得曲线位置在变化的时候更高效
.
.
3.给定曲线的边界参数
4.曲线速度、加速度加加速度变化分析及计算【通过控制时间实现】
情况1 :曲线的终点大于起点,即曲线是向前进的(q1>q0)
(1)判断double S曲线是否适合部署条件
首先需要判断位移h=q1 -q0是否满足最大速度vmax、最大加速度amax、最大加加速度jmax 的限制,极限情况就是纯加速或者纯减速的情况【防盗标记–盒子君hzj】
如果![]() 说明路径是可行的
说明路径是可行的
.
.
(2)满足最大速度的限制下,存在以下两种情况
运动被分成三个阶段分析
【按照加速度划分】
加速段:加速度线性增加到amax,然后减小到0
最大速度匀速段 :保持加速度为0
减速段 : 加速度减小到-amax 然后增加到0【防盗标记–盒子君hzj】
Case1:达到可以达到最大速度Vlim=Vmax

(1)先推测加速段、减速段时间
【通过加速度推测】
【加速段和减速段是对称的,时间也是一样的】
1、判断加速度是否达到最大加速度(a=amax或者a=-amax)
若达到了最大加速度amax/amin
加速段的时间公式【防盗标记–盒子君hzj】

减速段的时间公式

若未达到了最大加速度amax/amin
控制输出
【计算出时间和给定各个参数就可以计算】
【加加速度控制】对加速度进行一次求导
【加速度控制方法】加速度匀加速/匀减速Tj的时间(因为这时候加速度是线性量比较好控制)
【速度控制方法】对加速度量进行一次积分
【位置控制方法】对加速度进行两次积分
(2)再推测出匀速段的时间
【推测出是否达到最大速度】
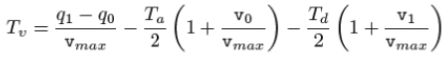
若Tv>0, 说明我们实际达到了最大速度,反之则没能达到最大速度
控制输出:
【加加速度控制】对速度进行两次求导
【加速度控制方法】对速度进行一次求导
【速度控制】按照最大速度运行tv的时间(此时速度的控制量是线性的)
【位置控制方法】对速度进行一次积分
.
.
Case2:达到未可以达到最大速度Vlin < Vmax
(1)先推测出匀速段的时间
在这个情况下,不存在匀速段,也就是匀速段的时间Tv = 0
控制输出:没有这个阶段的控制【防盗标记–盒子君hzj】
.
.
(2)再推测出加速段、减速段时间
【通过加速度推测】
【加速段和减速段是对称的,时间也是一样的】
判断加速度是否达到最大加速度(a=amax或者a=-amax)
判断条件
![]()
Ta:加速段周期
Td:减速段周期
如果 ![]() ,此时没能达到最大或者最小加速度【防盗标记–盒子君hzj】
,此时没能达到最大或者最小加速度【防盗标记–盒子君hzj】
若达到了最大加速度amax,加/减速段的时间公式
加速段和减速段是对称的,时间也是一样的
加减速轨迹段的时间Tj公式:
![]()
若未达到了最大加速度amax,加/减速段的时间公式
(1)有加速、减速的过程(Td>0且Ta>0时)
由于加减速不一定刚好对分,这样的不确定因素对求解其中的参数会比较困难,这里通过引入变量delta,通过逐步缩减amax值的方法进行近似计算规划轨迹的加减速段的时间Ta,Td.【防盗标记–盒子君hzj】
给定通过线性变化,慢慢减小a_max的值![]()
而在上述计算过程中,还可能会出现Ta,Td为负值的情况,这种情况下,则是该规划轨迹仅仅有加速段轨迹或者仅仅有减速度轨迹。【防盗标记–盒子君hzj】
在这种情况下,速度给定的初始值V0和V1的关系:v0>v1是计算成立的一个必要条件
.
.
(2)只有加速(v0>v1,Td<0时)

情况2 :曲线的起点大于终点,即曲线是向后退的(q0>q1)
【通用的情况】
(1)给定的曲线的位置、速度边界条件
![]()
.
(2)假设曲线方向
![]()
sign()函数功能是取某个数的符号(正或负): 当x>0,sign(x)=1;当x=0,sign(x)=0; 当x<0, sign(x)=-1
.
(3)把后退的方向转换到前进的方向,进而得到速度、加速度、加加速度的系统参数

(4)此时问题转化成了情况1,计算出结果之后再次转换,进而得到最终的位置、速度、加速度、加加速度控制输出
.
5.控制输出
加速段控制率
匀速段控制率
减速段控制率
技巧
在加/减速段用加速度控制,在匀速段用速度控制(因为这时候都是线性值)
.
.
(3)程序流程图
(4)二维源代码示例
clc;clear all;
%%
%NOTE: 速度轨迹规划初步实现
%① Vlimt=Vmax时,Tv>0;
%② Vlimt<Vmax时,Tv=0;Tv,velocity constant period
% 1)加减速混合轨迹;
% 2)仅加速轨迹 v0<v1;
% 3)仅减速轨迹 v0>v1;
%% 输入参数
q0=0;q1=10;v0=0;v1=-5;
vmax=5;amax=10;jmax=30;
n=1000 %总点数
%% 计算程序
[ta,td,tv,tj1,tj2,vlim,alima,alimd,jmax]=myfunC(q0,q1,v0,v1,vmax,amax,jmax,8)
duration=ta+td+tv;
dt=duration/n;
[uv,vel,acc,jerk]=DoubleS(n,q0,v0,q1,v1,ta,td,tv,tj1,tj2,vlim,alima,alimd,jmax,duration);
%% 绘图
myplot(uv,dt,duration,vel,vmax,acc,amax,jerk,jmax)
%——————————————————————————————————————————————————————————————————%
%% matlab 函数库
%% 绘图
function myplot(uv,dt,duration,vel,vmax,acc,amax,jerk,jmax)
t=dt:dt:duration;
subplot(4,1,1)
plot(t,uv,'r-','linewidth',1.5);
title('位移曲线');xlabel('时间t[s]');ylabel('位移[rad]');grid on;
subplot(4,1,2)
plot(t,vel,'b','linewidth',1.5);
hold on;plot([0,duration],[vmax,vmax],'m--');plot([0,duration],[-vmax,-vmax],'g--');hold off;
title('速度曲线');xlabel('时间t[s]');ylabel('速度[rad/s]');grid on;legend('vel','vmax','vmin')
subplot(4,1,3)
plot(t,acc,'g-','linewidth',1.5)
hold on;plot([0,duration],[amax,amax],'m--');plot([0,duration],[-amax,-amax],'g--');hold off;
title('加速度曲线');xlabel('时间t[s]');ylabel('加速度[rad/s^2]');grid on;legend('acc','amax','amin')
subplot(4,1,4)
plot(t,jerk,'k-.','linewidth',1.5)
hold on;plot([0,duration],[jmax,jmax],'m--');plot([0,duration],[-jmax,-jmax],'g--');hold off;
title('jerk曲线');xlabel('时间t[s]');ylabel('加加速[rad/s^3]');grid on;legend('jerk','jmax','jmin')
end
%%
function [uv,vel,acc,jerk]=DoubleS(n,q0,v0,q1,v1,ta,td,tv,tj1,tj2,vlim,alima,alimd,jmax,duration)
uv=zeros(1,n);
vel=zeros(1,n);
acc=zeros(1,n);
jerk=zeros(1,n);
h=q1-q0; %desired displacement h
jmin=-jmax;% vlim
% alimd=-alima;
for l=1:1:n
%t=(l*duration-1)/(n);
t=duration*(l-1)/(n-1);
% 1
if t<=tj1
uv(l)= q0 + v0*t + jmax/6*t^3;
vel(l)=v0 + jmax/2*t^2;
acc(l)=jmax*t;
jerk(l)=jmax;
% 2 (无匀速段时可省略)
elseif (t>tj1 )&&( t<ta-tj1)
uv(l)= q0 + v0*t + alima/6*(3*t^2-3*tj1*t+tj1^2);
vel(l)=v0 + alima*(t-tj1/2);
acc(l)=alima;
jerk(l)=0;
% 3
elseif (t>ta-tj1) && (t<=ta )
uv(l)= q0 +1.0/2*(vlim+v0)*ta - vlim*(ta-t) - 1.0/6*jmin*(ta-t)^3;
vel(l)=vlim + 1.0/2*jmin*(ta-t)^2;
acc(l)= - jmin*(ta-t);
jerk(l)=jmin;
% 4 ()
elseif (t>ta) && (t<=ta+tv )
uv(l)= q0 + 1.0/2*(vlim+v0)*ta + vlim*(t-ta);
vel(l)=vlim;
acc(l)=0;
jerk(l)=0;
% 5
elseif (t>duration-td) && (t<=duration-td+tj2 )
uv(l)= q1 - (vlim+v1)*td/2 + vlim*(t-duration+td) - jmax/6*(t-duration+td)^3;
vel(l)=vlim - jmax/2*(t-duration+td)^2;
acc(l)= - jmax*(t-duration+td);
jerk(l)= - jmax;
% 6
elseif ( t>duration-td+tj2) && (t<=duration-tj2 )
uv(l)= q1 - v1*(duration-t) + alimd/6*(3*(duration-t)^2-3*tj2*(duration-t)+tj2^2);
vel(l)= vlim + alimd*(t-duration+td-tj2/2);
acc(l)=- jmax*tj2;
jerk(l)=0;
% 7
elseif (t>duration-tj2) && (t<=duration )
uv(l)= q1 - v1*(duration-t) - jmax/6*(duration-t)^3;
vel(l)=v1 + jmax/2*(duration-t)^2;
acc(l)=- jmax*(duration-t);
jerk(l)=jmax;
end
end
end
%% 计算不同情况
function[ta,td,tv,tj1,tj2,vlim,alima,alimd,jmax]=myfunC(q0,q1,v0,v1,vmax,amax,jmax,flag)
if (vmax-v0)*jmax<amax^2 %amax is not reached
tj1=sqrt((vmax-v0)/jmax)
ta=2*tj1
else %amax is reached
tj1=amax/jmax
ta=tj1+(vmax-v0)/amax
end
if (vmax-v1)*jmax<amax^2 %amin is not reached
tj2=sqrt((vmax-v1)/jmax)
td=2*tj2
else %amin is reached
tj2=amax/jmax
td=tj2+(vmax-v1)/amax
end
tv=(q1-q0)/vmax-ta/2*(1+v0/vmax)-td/2*(1+v1/vmax)
if tv>0
vlim=vmax; % Case 1:vlimit=vmax
alima=jmax*tj1
alimd=-jmax*tj2
elseif tv<0 % Case 2:vlimit<vmax
tv=0
tj1=amax/jmax
tj2=tj1
tj=tj1
% deat=amax^4/(jmax^2)+2*(v0^2+v1^2)+amax*(4*(q1-q0)-2*amax/jmax*(v0+v1))
end
switch flag
case 0 %混合轨迹
deat=amax^4/(jmax^2)+2*(v0^2+v1^2)+amax*(4*(q1-q0)-2*amax/jmax*(v0+v1))
ta=(amax^2/jmax-2*v0+sqrt(deat))/(2*amax)%两个解
% ta=(amax^2/jmax-2*v0-sqrt(deat))/(2*amax) %ta<0
td=(amax^2/jmax-2*v1+sqrt(deat))/(2*amax)%两个解
% td=(amax^2/jmax-2*v1-sqrt(deat))/(2*amax) %td<0
case 1 %仅减速轨迹
deat=amax^4/(jmax^2)+2*(v0^2+v1^2)+amax*(4*(q1-q0)-2*amax/jmax*(v0+v1))
ta=(amax^2/jmax-2*v0-sqrt(deat))/(2*amax) %ta<0
td=(amax^2/jmax-2*v1+sqrt(deat))/(2*amax)%两个解
case 2
deat=amax^4/(jmax^2)+2*(v0^2+v1^2)+amax*(4*(q1-q0)-2*amax/jmax*(v0+v1))
ta=(amax^2/jmax-2*v0+sqrt(deat))/(2*amax)%两个解
td=(amax^2/jmax-2*v1-sqrt(deat))/(2*amax) %td<0
otherwise
return;
end
vlim=(q1-q0)/td;
alima=jmax*tj1;
alimd=-jmax*tj2;
vlim=v0+(ta-tj1)*alima;
vlim=v1-(td-tj2)*alimd;
%仅有加减速的情况
if (ta<0 && v0>v1) % Case 2-1:ta<0 &v0>v1 只有减速段
ta=0
td=2*(q1-q0)/(v1+v0)
tj1=0
tj2=(jmax*(q1-q0)-sqrt(jmax*(jmax*(q1-q0)^2+(v1+v0)^2*(v1-v0))))/(jmax*(v1+v0))
tv=0
alima=jmax*tj1
alimd=-jmax*tj2
% vlim=v0+(ta-tj1)*alima
vlim=v1-(td-tj2)*alimd
end
if (td<0 && v0<v1) % Case 2-1:td<0 &v0<v1 只有加速段
tv=0
td=0
ta=2*(q1-q0)/(v1+v0)
tj2=0
tj1=(jmax*(q1-q0)-sqrt(jmax*(jmax*(q1-q0)^2-(v1+v0)^2*(v1-v0))))/(jmax*(v1+v0))
alima=jmax*tj1
alimd=-jmax*tj2
vlim=v0+(ta-tj1)*alima
% vlim=v1-(td-tj2)*alimd
end
end
(5)三维的源代码解析示例
double S曲线的类及其参数
class DoubleSTrajectory3d {
public:
DoubleSTrajectory3d();
// 调用的API
//【核心--曲线计算】给定起始点、目标点、起始速度、终止速度,
// 计算各个周期时间和控制率(加速段加速度a_lima_、减速段加速度a_limd_、匀速段速度v_lim_)
bool setPath(const common::NavGoal3D& _start, const double& _initial_vel,
const common::NavGoal3D& _target, const double& _final_vel);
//获取double S曲线的运行总时间
double getTime();
//【核心--调用】输入当前时间,获取曲线的当前位置点,曲线调用的方式和B样条如出一辙
bool evaluate(double time, Eigen::Vector2d* current_point);
private:
double t_;
double a_max_;
double a_lima_; //加速段加速度
double a_limd_; //减速段加速度
double v_max_;
double v_lim_; //匀速段速度
double j_max_;
double t_j1_;
double t_j2_;
double t_a_;
double t_v_;
double t_d_;
Vector3d start_;
Vector3d end_;
Vector3d direction_vector_;
double v0_;
double v1_;
double s_;
};
double S曲线计算【单段曲线】
//【核心--曲线计算】给定起始点、目标点、起始速度、终止速度,
// 计算各个周期时间和控制率(加速段加速度a_lima_、减速段加速度a_limd_、匀速段速度v_lim_)
DoubleSTrajectory3d::DoubleSTrajectory3d() {}
bool DoubleSTrajectory3d::setPath(NavGoal3D& start,
initial_vel,
NavGoal3D& target,
const double& final_vel) {
//(1)初始化参数
start_ = start.position;
end_ = target.position;
v0_ = initial_vel;
v1_ = final_vel;
s_ = (start_ - end_).norm();//计算起点和终点的位移
if (s_ <= 1e-4) { //起点和终点的位移过短,退出
t_j1_ = 0.0;
t_j2_ = 0.0;
t_a_ = 0.0;
t_v_ = 0.0;
t_d_ = 0.0;
t_ = t_a_ + t_v_ + t_d_;
return true;
}
v_max_ = target.max_speed; //设置速度
a_max_ = target.max_acceleration; //设置加速度
j_max_ = DOUBLE_S_MAX_JERK; //设置加加速度
direction_vector_ = (end_ - start_) / s_; //计算三维方向向量
//(2)计算double S曲线
double d = v1_ - v0_; //计算起点和终点的速度差值
//1)判断double S曲线是否适合部署条件check feasibility
//即判断位移h=q1 -q0是否满足最大速度vmax、最大加速度amax、最大加加速度jmax 的限制。tj = cri2才符合
double cri1 = std::sqrt(std::fabs(v1_ - v0_) / j_max_);
double cri2 = a_max_ / j_max_;
double tj = std::min(cri1, cri2);
if (tj < cri2) {
if (s_ < (tj * (v1_ + v0_))) {
return false;
}
} else {
if (s_ < 0.5 * (v0_ + v1_) * (tj + std::fabs(v1_ - v0_) / a_max_)) {
return false;
}
}
//2)根据七段控制率开始计算曲线(加速阶段)
// case1:假设 v_lim == v_max
//加速段
if ((v_max_ - v0_) * j_max_ < a_max_ * a_max_) { // a_max not reached
//若未达到了最大加速度amax,加速段的时间公式
t_j1_ = std::sqrt((v_max_ - v0_) / j_max_);
t_a_ = 2 * t_j1_;
} else {
//若达到了最大加速度amax,加速段的时间公式
t_j1_ = a_max_ / j_max_;
t_a_ = t_j1_ + (v_max_ - v0_) / a_max_;
}
//减速段
if ((v_max_ - v1_) * j_max_ < a_max_ * a_max_) { // a_min is not reached
//若未达到了最大加速度amin,减速段的时间公式
t_j2_ = std::sqrt((v_max_ - v1_) / j_max_);
t_d_ = 2 * t_j2_;
} else {
//若达到了最大加速度amin,减速段的时间公式
t_j2_ = a_max_ / j_max_;
t_d_ = t_j2_ + (v_max_ - v1_) / a_max_;
}
//匀速段
//计算时间公式
t_v_ = s_ / v_max_ - 0.5 * t_a_ * (1 + v0_ / v_max_) - 0.5 * t_d_ * (1 + v1_ / v_max_);
if (t_v_ > 0) { //若Tv>0, 说明我们实际达到了最大速度,反之则没能达到最大速度
t_ = t_a_ + t_v_ + t_d_; //总时间=加速段时间+匀速段时间+减速段时间
//计算控制率输出
a_lima_ = j_max_ * t_j1_; //加速段加速度
a_limd_ = -1 * j_max_ * t_j2_; //减速段加速度
v_lim_ = v0_ + (t_a_ - t_j1_) * a_lima_;//匀速速度
return true;
}
/
//case2:假设 v_lim < v_max
// if not retured at this point, it means v_lim < v_max
while (1) {
//1)计算判断加速度是否达到最大加速度(a=amax或者a=-amax)的公式
t_j1_ = a_max_ / j_max_;
t_j2_ = t_j1_;
double& t_j = t_j1_;
double delta = std::pow(a_max_, 4) / std::pow(j_max_, 2) + 2 * (v0_ * v0_ + v1_ * v1_) +
a_max_ * (4 * s_ - 2 * a_max_ * (v0_ + v1_) / j_max_);
t_a_ = 0.5 * (a_max_ * a_max_ / j_max_ - 2 * v0_ + std::sqrt(delta)) / a_max_;
t_d_ = 0.5 * (a_max_ * a_max_ / j_max_ - 2 * v1_ + std::sqrt(delta)) / a_max_;
//2)判断此时没能达到最大或者最小加速度,加/减速段的时间公式
if (t_a_ > 2 * t_j && t_d_ > 2 * t_j) {
t_v_ = 0;
t_ = t_a_ + t_d_;
//计算控制率输出
a_lima_ = j_max_ * t_j1_;
a_limd_ = -1 * j_max_ * t_j2_;
v_lim_ = v0_ + (t_a_ - t_j1_) * a_lima_;
return true;
}
//3)若未达到了最大加速度amax,减速段的时间公式
if (t_a_ < 0) {
t_d_ = 2 * s_ / (v0_ + v1_);
t_a_ = 0;
t_j1_ = 0;
t_j2_ = (j_max_ * s_ - std::sqrt(j_max_ * (j_max_ * s_ * s_ + std::pow(v1_ + v0_, 2) * d))) / (j_max_ * (v1_ + v0_));
t_v_ = 0;
t_ = t_a_ + t_v_ + t_d_;
//计算控制率输出
a_lima_ = j_max_ * t_j1_;
a_limd_ = -1 * j_max_ * t_j2_;
v_lim_ = v0_ + (t_a_ - t_j1_) * a_lima_;
return true;
}
//3)若未达到了最大加速度amax,加速段的时间公式
if (t_d_ < 0) {
t_a_ = 2 * s_ / (v0_ + v1_);
t_d_ = 0;
t_j2_ = 0;
t_j1_ = (j_max_ * s_ - std::sqrt(j_max_ * (j_max_ * s_ * s_ - std::pow(v1_ + v0_, 2) * d))) / (j_max_ * (v1_ + v0_));
t_v_ = 0;
t_ = t_a_ + t_v_ + t_d_;
a_lima_ = j_max_ * t_j1_;
a_limd_ = -1 * j_max_ * t_j2_;
v_lim_ = v0_ + (t_a_ - t_j1_) * a_lima_;
return true;
}
a_max_ *= 0.9;
}
return true;
}
【核心–调用】输入当前时间,获取曲线的当前位置点,曲线调用的方式和B样条如出一辙
bool DoubleSTrajectory3d::evaluate(double t, Eigen::Vector2d* current_point) {
if (t < 0) {
t = 0;
}
if (t > t_) {
t = t_;
}
double s;
double v;
// 加速段,计算速度和位置
if ( t <= t_j1_) { //
s = v0_ * t + j_max_ * std::pow(t, 3) / 6.0;
v = v0_ + 0.5 * j_max_ * std::pow(t, 2);
}
else if (t <= t_a_ - t_j1_) {
s = v0_ * t + a_lima_ * (3 * std::pow(t, 2) - 3 * t_j1_ * t + std::pow(t_j1_, 2)) / 6.0;
v = v0_ + a_lima_ * (t - 0.5 * t_j1_);
}
else if (t <= t_a_) {
s = 0.5 * (v_lim_ + v0_) * t_a_ - v_lim_ * (t_a_ - t) + j_max_ * std::pow(t_a_ - t, 3) / 6.0;
v = v_lim_ - 0.5 * j_max_ * std::pow(t_a_ - t, 2);
}
//匀速段,计算速度和位置
else if (t <= t_a_ + t_v_) {
s = 0.5 * (v_lim_ + v0_) * t_a_ + v_lim_ * (t - t_a_);
v = v_lim_;
}
//减速段,计算速度和位置
else if (t <= t_ - t_d_ + t_j2_) {
s = s_ - 0.5 * (v_lim_ + v1_) * t_d_ + v_lim_ * (t - t_ + t_d_) - j_max_ * std::pow(t - t_ + t_d_, 3) / 6.0;
v = v_lim_ - 0.5 * j_max_ * (t - t_ + t_d_) * (t - t_ + t_d_);
}
else if (t <= t_ - t_j2_) {
double temp = t - t_ + t_d_;
s = s_ - 0.5 * (v_lim_ + v1_) * t_d_ + v_lim_ * temp + a_limd_ * (3 * std::pow(temp, 2) - 3 * t_j2_ * temp + std::pow(t_j2_, 2)) / 6.0;
v = v_lim_ + a_limd_ * (temp - 0.5 * t_j2_);
}
else {
s = s_ - v1_ * (t_ - t) - j_max_ * std::pow(t_ - t, 3) / 6.0;
v = v1_ + 0.5 * j_max_ * std::pow(t_ - t, 2);
}
//因为位置和速度是二维的,用三维向量计算出某一个方向的分量
Eigen::Vector3d p = start_ + s * direction_vector_;
Eigen::Vector3d vp = v * direction_vector_;
//位置
current_point[0][0] = p[0];
current_point[1][0] = p[1];
current_point[2][0] = p[2];
//速度
current_point[0][1] = vp[0];
current_point[1][1] = vp[1];
current_point[2][1] = vp[2];
return true;
}
获取double S曲线的运行总时间
double DoubleSTrajectory3d::getTime() {
return t_;
}
(6)总结
(1)double S 曲线怎么从二维扩展到三维?
(1)方法一:进行降维处理
(2)方法二:不会进行降维处理,三维计算曲线,最后面用一个三维向量计算出xyz方向的分量
.
(2)单段double S 曲线的计算于调用方法
double S 曲线输入的是曲线的边界条件,按照加速段、匀速段、减速段的周期计算出控制率(速度和加速度),通过输入 时间点就可以获取到曲线具体的位置、速度、加速度、加加速度信息【防盗标记–盒子君hzj】
.
(3)多段double S 曲线(全局航线)的计算于调用方法
把全部曲线划分为一段一段进行double曲线规划的,方法是把航线划分为一小段一小段先进行double S曲线的拟合,在把每一小段拟合好的曲线push到一个wps_list里面,从而wps_list就表征了拟合好的全局航线
.
(7)参考资料
https://zhuanlan.zhihu.com/p/267501745
https://blog.csdn.net/easy_R/article/details/103444453
《Trajectory Planning for Automatic Machine and Robots》
【防盗标记–盒子君hzj】
.
四、【地图的方法】
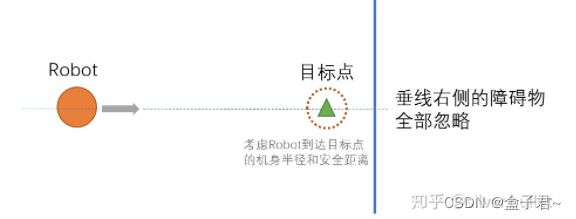
1、局部路径规划VFH、VFH+、VFH*算法(输入是局部栅格地图,输出下一步的运动方向)
(0)人工势场算法入门
一、算法思想

如上图所示,人工势场包括引力势场和斥力势场,在人工势场的作用力下,两个障碍物提供了两个斥力、目标提供了一个引力,在合力的作用下,机器人在避开障碍物的同时找到一条到达目标的可通行路径
.
二、算法的输入输出
输入的是目标点和障碍物的位置
输出的是机器人的合力受力方向(机器人运动的加速度轨迹,通过积分可以得到速度和位置轨迹,当然速度曲线我们可以人为给定,避免惯性问题)
.
三、算法流程
四、人工势场的改进
五、算法效果

全局路径搜索效果一般,平滑性不是特别好,需要进一步改进,故人工势场的方法多用于局部避障优化
.
(1)Virtual Force Field (VFF)算法
VFF算法是VFH算法的前身,类似人工势场法。
1、主要的步骤
(1)步骤一:传感器更新占据栅格地图
根据测距传感器测量模型更新感兴趣的栅格。不同的传感器可以设计不同的测量模型和更新方法。

(2)步骤二:计算活动窗口内的合力
设定活动窗口ROI,在里面计算障碍物排斥力的合力和前进目标的吸引力。排斥力和吸引力的合力就是运动方向。其中,排斥力的大小与栅格被障碍物占据的确定程度成正比,与距离成反比。
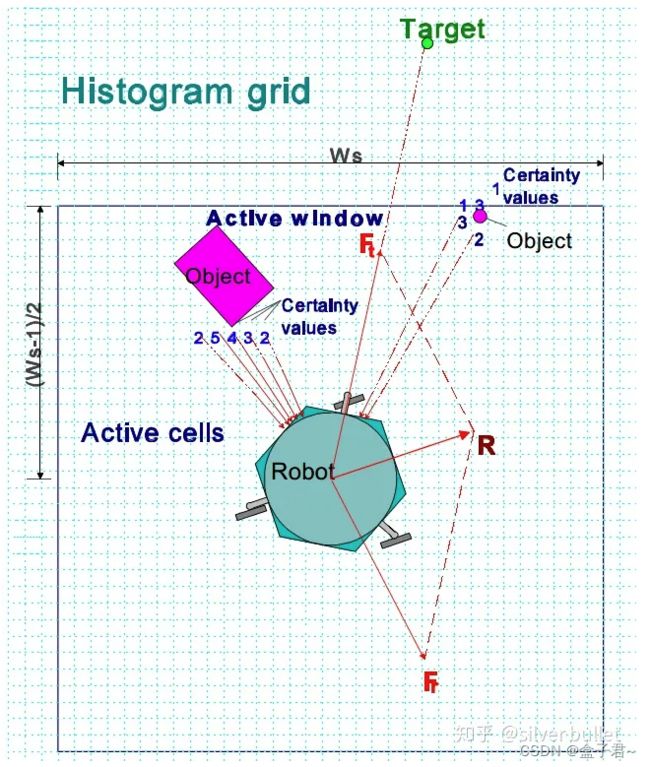
2、VFF算法问题
主要原因是原理上的缺陷——大量障碍物点的数据被抽象成一个排斥力的大小和方向,造成了信息损失。
1、和人工势场法相同的局部极小值。
2、无法通过狭窄的障碍物间隙。
3、传感器测量的不确定性、坐标和占据值的离散变化,导致运动方向易抖动。
.
.
(2)VFH算法–用地图的方法做运动规划
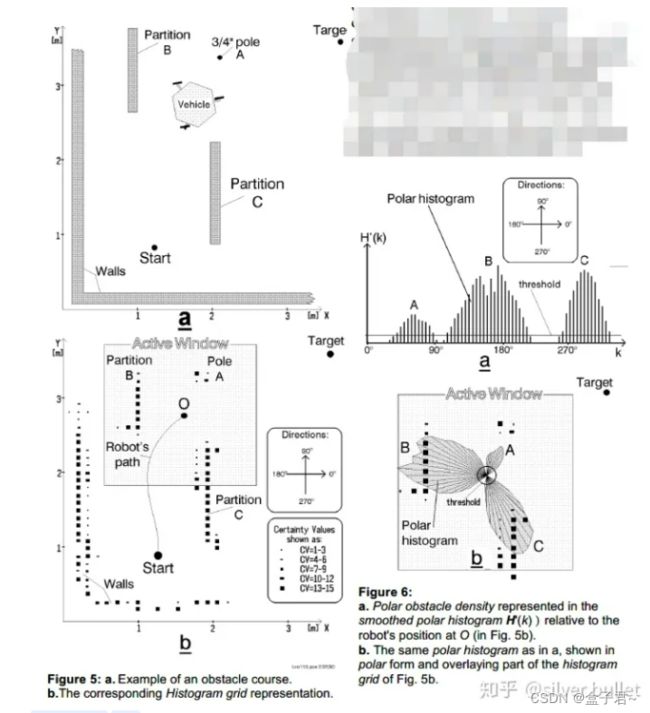
1.VFH算法的中心思想–把栅格图转换成统计直方图的地图格式
VFH同样依赖测距传感器更新地图,将所有栅格的被障碍物占据情况、对运动方向的影响,通过统计直方图表示。这样的表示非常适合不准确的传感器数据,并适应多传感器读数的融合。
2.VFH的3层数据及数据转换步骤
(1)VFH的3层数据
1、顶层:根据传感器观测数据更新的二维栅格地图;
2、中层:一维的极坐标直方图polar histogram,就是将VFF的活动窗口ROI按角度均分为多个sector,每个sector用polar obstacle density表示对应的角度范围内障碍物的占据情况(密度、数量、置信度等);
3、底层:VFH控制输出的运功方向。
实际场景-栅格地图-活动窗口-直方图对应关系示例
确定运动方向
.
.
(2)数据转换步骤
1、将ROI的每个栅格用obstacle vector表示,方向是cell到robot center的方向,大小与确定程度成正比、与到robot center的距离成反比。
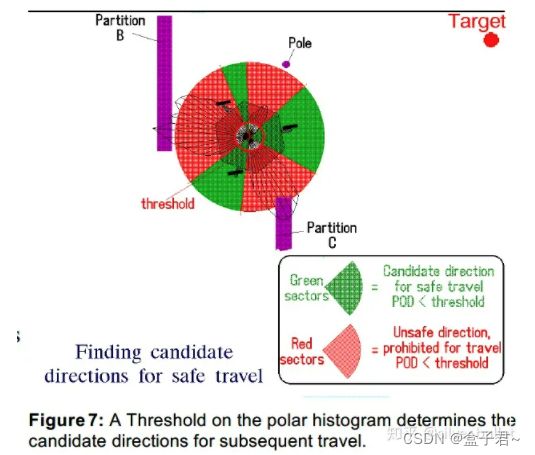
2、计算polar obstacle density,就是落在相同sector的obstacle vector的大小叠加。这里可以用加权平均来平滑。
3、根据polar obstacle density的峰谷、density的阈值,挑选出与前往目标点的方向最吻合的谷。取谷的中间角度作为运动方向。可以通过全局规划设定自适应阈值。
4、根据当前运动方向上的density大小,调整运动速度。输出结果。
3.VFH应用上的局限
4.VFH的优点
1、对比VFF,VFH优势是可以平滑的在障碍物密集的区域行驶,响应快,无需停止等待规划。
2、VFH可以输出速度、方向,运动速度受传感器观测和更新频率限制。如果陷入局部极小值,论文给出了方向偏离检测方法,可以调用全局规划脱困。
5.代码实现
https://playerstage.sourceforge.net/doc/Player-2.0.0/player/group__driver__vfh.html
.
.
(3)VFH+算法
1.VFH+算法的实现步骤
(1)以机器为中心建立局部地图坐标系,将传感器观测到的信息更新到窗口ROI,建立local gridmap
==>local gridmap
(2)转换到3种直方图中
==> Primary polar histogram
Primary polar histogram。将圆形的活动窗口中每个cell的obstacle vector转换为polar histogram中的polar obstacle density,计算density时不止考虑一个sector内的cells,还要考虑按机器人半径扩展cell所覆盖的cells。在设计density的计算公式时,要考虑栅格被占据概率、离robot中心的距离等因素的重要程度如何分配。
.
==> Binary polar histogram
Binary polar histogram。利用迟滞双阈值,将Primary polar histogram转换为用0、1表示是否可行走的二值图。
.
==> Masked polar histogram
Masked polar histogram。在Binary polar histogram的基础上,根据当前运动状态(v,w)预测轨迹(主要考虑转弯半径),搜索与该轨迹有重合的左右边界cell的角度(包含扩展的cell),确定可行sectors的左右边界,更新出Masked polar histogram。
.
==> Moving direction
在可行sectors中,采样候选的运动方向。使用cost function在一些候选方向中选择最好的输出。代价函数主要考虑:1是候选方向与目标方向的差异;2是候选方向与轮子朝向的差异;3是候选方向与历史输出的差异等等。
.
.
2.VFH+算法的优点
VFH+在代码实现时比较简单
相比VFH,主要的提升在于更平滑的轨迹和更好的可靠性,具体体现为:
1、将polar histogram转换为二值直方图binary polar histogram时,使用迟滞双阈值,去除抖动;
2、在计算polar obstacle density时考虑了机器人尺寸(半径),相当于做了障碍物膨胀,不再需要像VFH给低通加权平均方法调参;
3、考虑了机器人的运动学模型和当前运动状态,筛除了障碍物挡住机器人运动轨迹的sectors,建立masked polar histogram,相当于做了碰撞检测;
4、使用代价函数来选择最优前进方向。
.
.
3.VFH+算法应用中主要有2个问题
1、根据VFH+的原理和步骤可以看出,其只能输出下一步的运动方向,由当前运动姿态转换到该运动方向的线速度、角速度等动态信息,均无法给出。实际应用中,可以根据输出角度与当前朝向、目标朝向等的差异来确定速度,比如转角越大,角速度越大,线速度越小。但终归有失严谨,运动平滑性较差,更谈不上轨迹规划。因此,比较合适用来在障碍物较多的环境中指出脱困的方向,可以作为其他运动规划控制方法的一个预处理步骤和输入。
2、VFH+使用了障碍物栅格相对Robot中心的方位来直接限定运动方向,使用了障碍物栅格距Robot中心的距离来计算density,间接反映对运动的影响程度。但因为有Primary polar histogram向Binary polar histogram的二值化过程,受阈值影响极大,其实距离信息也基本损失了。这导致阈值难以调参,更重要的是难以接近靠近障碍物的目标点,因为目标点方向可能会被排除掉。虽然可以通过减小局部地图窗口范围缓解,但效果一般。
针对第2个问题,我采用了如下策略来解决,实测效果较好。
1、若障碍物位于Robot和目标点之间,按照VFH+避障。
2、若障碍物在Robot向目标点连线的延伸线上,且离目标点很近,按照VFH+计算density。当Robot离目标点很远时,density较小,Robot仍可以继续靠近目标点;逐渐变近时,density增大直到VFH+判断目标点不可达,向上通知全局规划器。
3、若障碍物在Robot向目标点连线的延伸线上,且离目标点很远,忽略其对Robot运动的影响。
4.代码实现
可惜的是,ROS中并没有VFH算法的代码
github.com/AugustoPB/vfh_local_planner
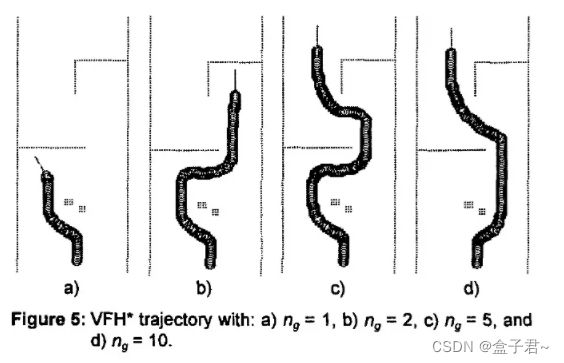
(4)VFH*算法
对比VFH+,VFH*能更好的处理需要机器人大转向或停下来的场景,比如死胡同。其实就是在VFH+输出的基础上,像RRT那样,迭代运行VFH+来向前扩展多个节点,从而引入更接近全局的信息。论文中详细讲述了扩展步长、步数、不同代节点的代价函数设计、权重选取等调参细节。至关重要的参数是向前扩展的距离ng,如图4中所示,会直接影响到全局信息的比例、运算量的大小。
我认为避开大规模的障碍物、死胡同等,应该由全局规划器来做。调用规划算法的业务逻辑应该检测到环境变化、位姿偏离过大等异常,间歇性或周期性的调用全局规划器重新规划,而不是像VFH*这样。与其多轮次的去扩展,不如设计好全局规划、局部规划、状态监测、异常处理的关系。这是一个系统性的问题,而不是局部规划的问题
.
#### (5)人工势场做避障案例--似然场的快速避障算法 1、似然场的快速避障算法 [https://blog.csdn.net/Travis_X/article/details/116307098](https://blog.csdn.net/Travis_X/article/details/116307098) [https://www.bilibili.com/video/BV17B4y1c7Sb?spm_id_from=333.999.0.0](https://www.bilibili.com/video/BV17B4y1c7Sb?spm_id_from=333.999.0.0) [https://www.bilibili.com/video/BV1464y1U7H6?spm_id_from=333.999.0.0](https://www.bilibili.com/video/BV1464y1U7H6?spm_id_from=333.999.0.0) [https://www.bilibili.com/video/BV1744y1C7pp?spm_id_from=333.999.0.0](https://www.bilibili.com/video/BV1744y1C7pp?spm_id_from=333.999.0.0)
.
参考资料
论文
http://www-personal.umich.edu/~ykoren/uploads/The_Vector_Field_HistogramuFast_Obstacle_Avoidance.pdf
https://ieeexplore.ieee.org/abstract/document/677362
https://ieeexplore.ieee.org/abstract/document/846405
链接
文献阅读之机器人局部路径规划Vector Field Histogram算法(VFH)
局部路径规划VFH+ VFH*算法