MUSICA(多尺度图像对比度增强)算法的简要原理及VC实现
MUSICA的专利文档:MUSICA_patent - Original document.pdf
程序源码下载:IPLab_MUSICA.rar
算法原理:
图像增强的一般方法是对比度拉伸和直方图均衡,这两种方法对于灰度级过于集中, 还有大量的灰度级没有充分利用的情况下比较适用,并且这两种方法都是基于直方图的变换,和像素的位置信息无关。假设有原始信号如(a),可看出细节信号(高频,例如指纹、衣服褶绉这样的细节)集中在较窄的灰度范围内,人眼很难分辨。并且细节信号集中的灰度范围在整个灰度级空间内,使用对比度增强和直方图均衡无法对不同的区域内像素进行不同程度的放大或者缩小。因此就有了MUSICA(Multi-Scale Image Contrast Amplification),可以翻译成多尺度图像对比度增强。
基本的原理是先提取细节信息,然后对细节信号进行增强放大,然后再重构到原图中。局部细节信息的提取现在研究的热点一直都是小波分解。
暂且不管理论,先从实际运用的角度来看。如图(b),假设对信号进行平滑滤波,可以得到新的蓝色信号。可以认为蓝色信号是对原信号的低分辨率近似,保留了整体的特征而丢弃了高频的细节信号,例如要分析图像的整体特征就要使用近似信号以排除高频(可能是噪声)的干扰。
那么如图(c),原信号减去近似信号,得到的就是高频信号,也就是细节信号(当然也可能是噪声)。
然后对(c)进行增强,最简单例如放大2倍,或者进行log变换得到(d)。
然后把(d)加回到近似信号上,重构出增强后的原信号,如(e)所示。可以看到,图像的整体特性没有改变,两个细节集团的细节信号被放大了,适合人眼辨认。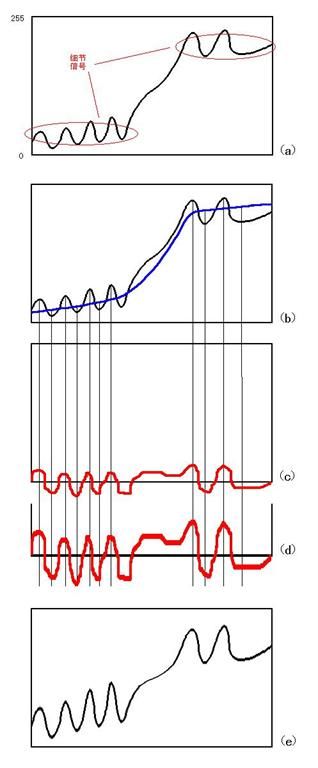
图1
这个算是从最直观的角度来考虑算法原理,只是一种近似的抽象,实际过程需要更多更具体的考虑,同时这也是个人的理解,会有偏颇的地方,留待完善。
然后,总得给出点具体的原理和算法的实际步骤。详细的说明可以从MUSICA的专利文档里获得,这里给出个人角度的理解和说明。
首先要从小波说起,直观地看,小波分解将(w*h)的图像分解成4个(w/2 * h/2) 的子图,其中1个为近似图像,3个为小波系数矩阵。然后对近似图像进行下一级的分解。如下图,A为原图的低分辨率近似图像,D为小波系数,D1、D2、D3的物理意义可以看作是水平、垂直、以及对角方向的细节矩阵。小波的重构是这个分解过程的逆过程,使用4个低分辨率的子图重组成一个高分辨率的图。这部分知识最好看看小波的教科书,可以比较全面了解小波的特点。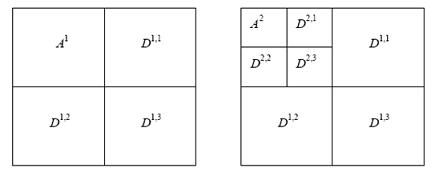
图2
直观地看小波分解,近似图像就是对原图的一个低分辨率的近似,保留图像的整体特征,而小波系数矩阵,就是低分辨率图像和原图的之间的差异,就是高频的信号,也就是细节。通过这样的分解,可以得到各个分辨率上的细节,目的是使某种分辨率下难以区分的特征在另一种分辨率下将很容易被区分和检测。人的眼睛可以自动聚焦来选择最佳的分辨率对眼前的景物进行分辨,而小波也就是因为类似人眼而受到很多重视。还有一个重要的概念是小波分解的小波,可以理解为用来分解图像而使用的小波基。直观地看,不同特性的小波基分解同一个图像,得到近似图像应该差不多,而提取得到的细节矩阵则反映的图像细节则有所差异。关于小波基的选择以及各种小波基特性的物理含义一直没有查找到比较好的解释。有一种解释是,某种小波基对某类特征的图像得到的小波系数矩阵比较有代表性,例如xxx1小波对图形组合简单的图像效果比较好,而xxx2小波对噪杂的自然图像好,xxx3对条纹状图像好...这仅是一个同学间讨论的假设,有待查证。
但是MUSICA里使用的不是这种分解,而是使用高斯图像金字塔,在Rafael C. Gonzalez.的 Digital Image Processing.(电子工业出版社. 2004)一书里有介绍,这里引用其中的两个图来说明,前面提到的下波分解作为数学的基础,教材比较多,容易深入。
高斯图像金字塔也是小波分解的一种,它生成一个w/2*h/2的低分辨率近似,和一个与原图等大的残差距阵(也就是高频细节)。图中的抽样(2↓)指对w*h的图像进行隔行采样,得到w/2*h/2的子图。内插器(2↑)则将w/2*h/2的图像行列间插入一个值扩展成w*h的图像,插入的值可以是0,或者是左右行的均值等方式。近似滤波和插入滤波就是所选择的小波基转化的滤波器组形式,这里选择的是高斯滤波器,滤波器的参数在专利文档里提供了一组经验参数,但是到具体设备上还需要根据实际成像的噪声等情况重新计算过才能达到较优的结果。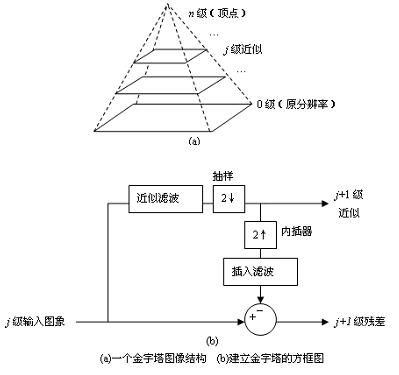
图3
专利文档提供得整体算法框图如下: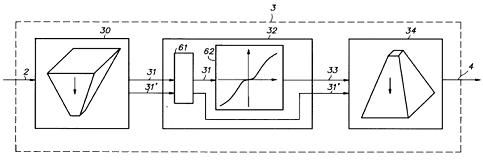
图4
2为输入图像,30为j级图像金字塔的分解过程,得到31为所有的残差矩阵,31'为图像的第j级近似。61缓存图像(对具体设备有意义吧)和62并对31进行s型函数的查表变换。34为重构过程,将变换后的残差距阵33和j级近似31'重新组合成增强后的图像4,输出。
根据这个流程,就可以开始考虑算法的程序实现了。
在开始在pc机上编程之前,需要说明几点:
首先是算法原理中影响效果的几个部分。一是62里s型函数的选择。增强算法都有会带来噪声也一同增强的副作用,专利文档里讨论了这个问题,选择y=m*(x/m)p的指数变换,p的取值会对增强的频段产生影响,合理选择p、进行分段选择不同的p,可以抑制噪声的增强。二是30分解过程和34重构过程,这个其实属于小波分解的部分,分解的级数、分解步骤和小波基的选择(这里就是滤波器参数的选择),会对分解得到残差距阵产生影响,得到的残差距阵是否具有有效细节的代表性,能否有效过滤噪声,是这里的关键。编程中可以将一些参数设置成变量,使用配制文件输入,则可以将算法的研究和实现分开。专利文档中对这两个方面也进行了讨论,可以参考深入。
然后还需要说明的一点的是,在pc上实现这个算法可能并不适合,一般都是在医疗设备上直接实现这个算法(嵌入式系统或者是某种特殊固件),使用关键字“AGFA MUSICA”可以在google上找到些相关资料。但是在这里并不考虑这点,仅把MUSICA作为一道有趣的算法题目,结合一些图像处理的知识努力去得到最优解。有相关背景的朋友也希望可以介绍一下相关专业的知识,那样就更有趣了。
程序源码下载:IPLab_MUSICA.rar
整体的流程还是比较简单的,问题是图像处理中的一些细节,例如滤波时边界的处理,图像抽样时w或者h为奇数时w/2(h/2)的取值,也就是离散整数的取整误差问题。还有些编程时内存分配的问题,临时缓存的分配等。但是不考虑得太复杂都使用最常用的方式,以上仅将大概的问题列出,碰到时候需要注意。
入口函数伪代码:
void GDIPlusImage::IPFuncMUSICA()
{
O = 原始图像;
for(分解级数)
{计算每级的长宽保存到矩阵S;}
ImageGrey24To8(O);//灰度化,仅对灰度图象进行处理
X = MUSICA_Decomposition(O,S);//分解,得到X为所有的图像按S里的顺序排列,30
X = MUSICA_Mapping(X,S);//对分解图像进行变换,32
O = MUSICA_Reconstruction(X,S);//重构,得到增强后的图像,34
ImageGrey8To24(O);//转化成24为图,显示、后继处理起来方便,仅此而已
}
MUSICA_Mapping(X,S)函数相对简单,只需要对S中的残差距阵进行灰度级的查表替换,替换的表根据s型函数事先构造好,其过程类似进行反色处理,可以参考前面的文章。可以考虑将替换表的构造独立出来,通过参数传递,方便改进。
MUSICA_Decomposition分解和MUSICA_Reconstruction重构过程相对复杂,而且专利文档中提供了几种改进后的分解重构过程。对于编程实现来说其实本质都相通,因此所附程序中实现了专利文档中的4.a和4.b,也就是最简单的一种。仅对4.a分解的实现进行说明,4.c重构为逆过程,参考源代码。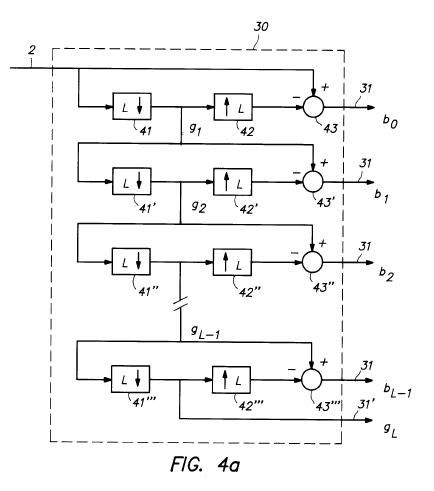
图5
一次分解流程:
1) 对X进行一级分解,X拷贝到buffer
2) 对buffer进行平滑滤波
3) buffer隔行抽样得到下一级的近似图X+1
4) 近似图X+1隔行插值0到buffer
5) 进行滤波参数乘4(对置0行列的补偿)的平滑滤波
6) X减去平滑后的buffer得到残差图像保存于X
这样就完成一次分解,然后再对X+1进行下一级的分解。
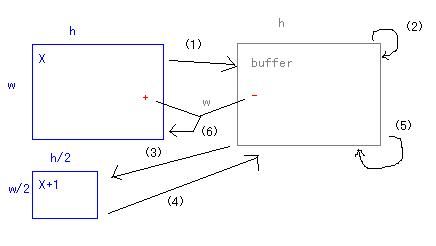
图6
所附程序在xp+vs.net2003下编译运行通过,程序运行后打开工程目录下的图片,点击快捷按钮1或者菜单项“图像处理-〉MUSICA”,然后要稍等一会,处理速度比较慢。工程目录下有两张示例图片,“心脏-交响乐处理前.jpg”为原始成像图片,“心脏-交响乐处理后.jpg”是一位老师给我的在专业设备上处理过后的结果图,作为和程序运行结果的比较。当然,程序运行的结果比它差很多,但是基本方向是对的,专利文档里还有很多改进的步骤和参数的择优都未实现,有兴趣的朋友自己动手。:)