SimCSE：用于句子嵌入的对比学习

引言

SimCSE来自论文：SimCSE: Simple Contrastive Learning of Sentence Embeddings，将对比学习思想引入了sentence embedding，并超过了同年很多无监督或有监督的语义相似度计算任务的表现。

学习自然语言的通用语义表示一直是NLP的基础任务之一，当2019年的SBERT出现后，语义相似度计算就变得进展缓慢，SBERT是一个基于BERT的孪生网络（SBERT属于早期的NLP对比学习模型），SimCSE改进对比学习的样本构建策略，大幅度提高了有监督和无监督语义匹配的表现。

对比学习Contrastive Learning

对比学习的目标就是拉近相似样本，推开不相似样本。使用对比损失的关键问题是如何构造$(x_i,x_i^{+})$正样本对。对比学习最早起源于计算机视觉的原因就是图像的正例$x_i^{+}$容易构造，比如裁剪，翻转，扭曲都不会影响图像的语义。对于结构高度离散的自然语言则很难构造语义一致的$x_i^{+}$，前人采用了一些数据增强方法来构造$x_i^{+}$，比如同义词替换，删除不重要的词，语序重排等，但这些都是离散的操作，很难把控质量，容易引入与类似负样本分布的"噪声"，这导致模型不容易从正负对中学习到正确的语义信息。

对比学习的目标是从数据中学习到一个优质的语义表示空间，通常，使用两个指标评价表示空间的质量：alignment和uniformity。其中alignment计算$x_i$和$x_i^{+}$的距离：$$l_{align}=E_{(x,x^{+})\sim p_{pos}}||f(x)-f(x^{+})|{|}^2$$其中，$p_{pos}$为正样本对的分布，$f(\cdot )$为编码器；

uniformity计算语义向量整体分布的均匀程度：$$l_{uniform}=log{E}_{(x,y)\sim p_{data}}exp(-2||f(x)-f(y)|{|}^2)$$其中，$p_{data}$为所有数据的分布。我们希望这两个指标都尽可能低，一方面希望正样本要挨得足够近，另一方面语义向量要尽可能地均匀分布在超球面上，因为均匀分布信息熵最高，分布越均匀则保留的信息越多，“拉近正样本，推开负样本”实际上就是在优化这两个指标。

SimCSE思想

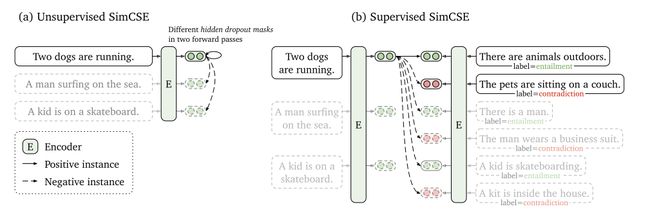
图a为无监督的SimCSE，在输入端，批处理中构建的都是负样本关系；图b为有监督的SimCSE，在输入端，将蕴含（前提假设）作为正样本，将矛盾以及其他实例作为负对。

无监督下的SimCSE

如果直接用BERT的句向量做无监督语义相似度计算，效果会很差，任意两个句子的BERT句向量的相似度都很高，其中一个原因是句向量分布的非线性和奇异性，BERT-flow通过Normalizing将向量分布映射到规整的高斯分布上，BERT-whitening对向量分布做了PCA降维消除冗余信息，但是不能解决非线性问题。

正好，对比学习的目标之一就是学习到分布均匀的向量表示，因此我们可以借助对比学习间接达到规整表示空间的效果，这又回到了正样本构建的问题上来，而本文的创新点之一正是无监督条件下的正样本构建。

在标准的Transformer中，dropout mask被放置在全连接层和注意力求和操作上，设$h_i^z=f_{\theta }(x_i,z)$，其中，$z$是随机生成的dropout mask，由于dropout mask是随机生成的，所以在训练阶段，将同一个样本分两次输入到同一个编码器中，可以得到两个不同的向量表示$h$和$h^{\prime }$，将$h^{\prime }$作为正样本，则模型的训练目标为：$$l_i=-log\frac{exp(sim(h_i,h_i^{\prime })/t)}{{\sum }_{j=1}^{N}exp(sim(h_i,h_j^{\prime })/t)}$$其中，$t$为温度系数，$sim(\cdot )$为计算向量相似度的函数，这种通过改变dropout mask生成正样本的方法可以看作是数据增强的最小形式，因为原样本和生成的正样本的语义是完全一致的，只是生成的embedding不同而已（利用dropout实现保持语义等价的自然语言数据增强）。

作者比较了这种简单的正样本生成方式和其他显式的数据增强方式，从维基百科中随机抽取十万个句子来微调BERT模型，并在STS-B数据集上测试，实验结果如下：

其中，None是作者提出的随机dropout mask方法，其余方法均是在None的基础上改变$x_i^{+}$的输入，追加显式的数据增强方式都会导致性能的大幅度下降。作者对比了这样的自监督方式和NSP目标的训练结果，如下表所示：

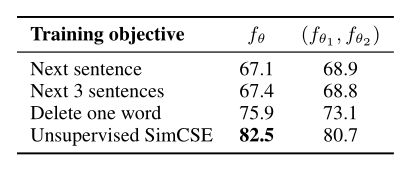
将NSP作为正样本的构建方法明显不够有效，远不如采用删除一个词或者无监督SimCSE的构建方式。另外，对于语义相似度计算的任务，共享编码器的效果更好。

下面研究为何无监督SimCSE是有效的。首先，作者尝试改变dropout rate，发现默认的比率0.1是最好的，去掉dropout（表中的0.0）或者固定dropout mask（表中的Fixed 0.1）后模型性能都会出现大幅度下降，因为这种情况下相当于$x_i$和$x_i^{+}$是完全一样的，模型除了增加计算量，并不能学习到额外的对比信息。

之前提到了衡量对比学习质量的两个指标，作者用这两个指标测试了不同模型训练过程中保存的ckeckpoints，可视化结果如下图：

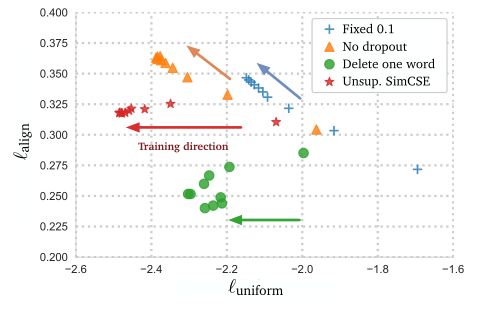
可以发现所有模型的uniformity都有所改进，表明预训练BERT的语义向量分布的奇异性被逐步减弱，而与Fixed dropout mask和No dropout相比，SimCSE能在规整分布的同时保持正样本的对齐，与Delete one word相比，虽然alignment比不上Delete one word，但由于其分布更加均匀，因此SimCSE总体性能更高。

有监督下的SimCSE

上面讨论了无监督SimCSE的优秀表现，在有监督的条件下，SBERT将NLI数据集作为一个三分类任务来训练，这种方式忽略了正样本和负样本之间的交互，而对比学习可以让模型感知到更丰富的细粒度语义信息。

首先考虑如何构造训练数据，其实很简单，直接获取数据集中的正负样本，将NLI数据集中的entailment作为正样本，conradiction作为负样本，加上原样本premise组合为$(x_i^{+},x_i^{-},x_i)$，损失函数表示为：$$l_i=-log\frac{exp(sim(h_i,h_i^{+})/t)}{{\sum }_{j=1}^N(exp(sim(h_i,h_j^{+})/t)+exp(sim(h_i,h_j^{-})/t))}$$其中，$x_i^{-}$可以看作hard negatives。

---

与无监督SimCSE进行对比，不管是有监督还是无监督的对比学习，SimCSE其实都是基于编码后的embedding构建正负样本，此处可以引出一个想法：也许基于embedding的数据增强才是适合NLP的数据增强，因为在embedding上做数据增强呈现出较小程度改变语义信息的趋势（但要注意编码器的计算规则，我们还是不能随意去改变embedding）。

---

作者分别尝试在不同的语义匹配数据集（QQP、Flickr、ParaNMT等）上训练模型，在STS-B上测试模型，结果如下：

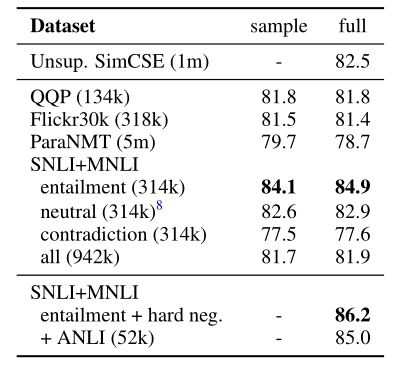
其中sample列表示采样相等样本量训练的结果，full表示使用完整数据集训练的结果，作者发现NLI训练出来的模型性能是最好的，这是因为NLI数据集的质量本身很高，正样本词汇重合度非常小(39%)且负样本足够困难，而QQP和ParaNMT数据集的正样本词汇重合度分别达到了60%和55%。

连接各向异性Connection to Anisotropy

近几年不少研究都提到了语言模型生成的语义向量分布存在各向异性的问题，这极大地限制了语义向量的表达能力，缓解这个问题的一种简单方法是加入后处理步骤，比如BERT-flow和BERT-whitening将向量映射到各向同性的分布上，而本文作者证明了对比学习的训练目标可以隐式地压低分布中的奇异值，提高uniformity。所以得出一个简单的小结：预训练模型的新训练范式也许应该是基于对比学习的。

而我个人也衍生了一些新的思考：合适的预训练模型或许应当是以聚类为背景的，对比学习可以帮助我们去提高聚类的质量，为了得到一个良好支持下游任务的模型，我们应当学习可用于聚类的语义向量。

分析

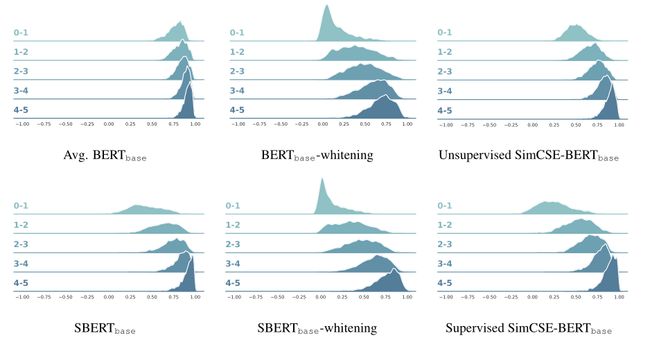
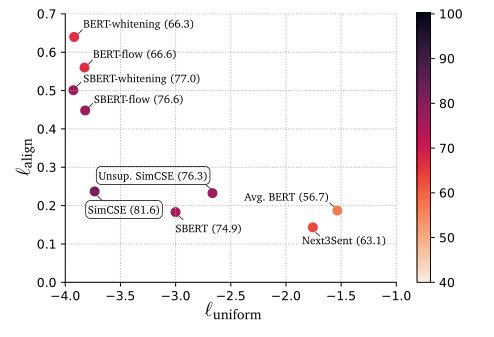
最后作者测试了现有模型的alignment和uniformity，如下图所示，可以发现性能更优的模型通常有着更好的alignment和uniformity，BERT虽然有很好的alignment，但uniformity太差，而基于后处理的BERT-flow和BERT-whitening又恰恰走向了另一个极端，作者提出的SimCSE则是对这两个指标的一个很好的平衡，加入监督信号训练后，SimCSE的两个指标会同时提升。

将上面提到的这三类模型的预测分布做一个可视化，如下图所示，我们可以发现BERT的区分度很差，几乎所有句子对的相似度都在0.7以上，而加上whitening虽然更有区分性，但又增大了整体分布的方差，而SimCSE正是这两者的平衡点，在保持区分度的同时又保持整体分布的集中度。（下图中，句子对根据Ground truth评分，被分成5组，序号越高代表越相似）