【计算机图形学】直线的两种生成算法(DDA算法、Bresenham算法)
直线的两种生成算法(DDA算法、Bresenham算法)
文章目录
-
-
- 1.计算机绘制直线的原理
- 2.DDA算法的原理与实现(基于matlab)
- 3.Bresenham算法的原理与实现(基于matlab)
-
1.计算机绘制直线的原理
在计算机中,直线的显示并不是连续的,而是离散的点,这是由光栅化的本质决定 的。我们可以把屏幕理解为阴极射线管光栅显示器,这个显示器是由离散可发光的有线 区域单元(像素)组成的矩阵。确定最佳逼近某直线的像素的过程通常叫做光栅化。对于 水平线、垂直线以及 45°线,选择哪些光栅元素是显而易见的,而对于其他方向的直线, 像素的选择就很困难。因此,选择一个重要的算法来实现直线的绘制显得很有必要。
2.DDA算法的原理与实现(基于matlab)
DDA 算法是直线算法里最为简单的算法,它的基本思想是高数里的微分算法:
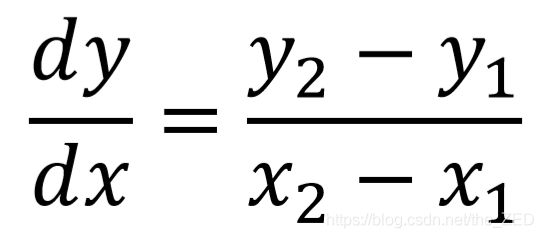
其有限差分近似解为:
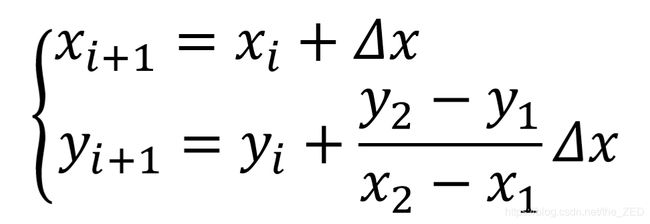
根据这个算法,我们可以将某条线段的两个端点作为输入,并利用这两个端点来将此线段进行微分(迭代求值),在每轮迭代中,将微分得到的每个点单独绘制。最终,所有单独绘制的点就构成了我们所需要绘制的直线。
下面给出用matlab实现该算法的完整代码:
function main %测试函数
clc
clear;
DDA(0,0,30,40,'r') %勾三股四弦五
function DDA(x1,y1,x2,y2,color) %DDA算法
dx=(x2-x1);
dy=(y2-y1);
step=max(abs(dx),abs(dy));
deltax=dx/step;
deltay=dy/step;
x=x1;
y=y1;
hold on
for i=1:step
scatter(round(x),round(y),'.',color) %绘出当前点
x=x+deltax; %更新x
y=y+deltay; %更新y
end
plot([x1,x2],[y1,y2]) %直接绘制原线以对比
grid minor %添加网格
hold off
运行后得到的效果如下:
上图展示的是在给定较短线段时(长度为50个像素),采用DDA算法绘出的直线情形(上图中的红点部分),其中的蓝色线段是这条线段本身(真实线段)
接下来若将该点设置长一些,即将上面的测试代码改为如下:
function main
clc
clear;
DDA(0,0,100,75,'r') %勾三股四弦五
则此时的成像效果如下:
上图中的红点即为DDA算法绘制的给定线段,而其中的黄线则为真实线段
可以发现此时点的密集程度大大增加,成像效果相较于上面也就好一些。
3.Bresenham算法的原理与实现(基于matlab)
原理:
这里仅展示最简单的一种情况(直线斜率在区间 (0,1)之间的),其他情况可以类似推导。
设当前像素点为 P(xp,yp),下一像素点有两种选择 P1 或 P2,设P1、P2 的中点为 M(xp+1,yp+0.5),Q 为所画直线与直线 x= xp+1 交点,如下图所示:
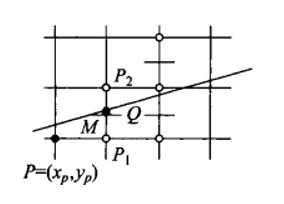
当Q在M上方时,下一像素点取P2;当Q在M下方时,下一像素点取P1。
实现:
① 首先设待画直线的起点和终点坐标分别为(x1,y1) 、 (x2,y2),则根据起点和中点坐标可以得到该直线的斜率为k=(y2-y1)/(x2-x1)。我们知道直线方程可以用F(x,y)=ax+by+c=0的形式来表达,此时该直线的斜率k=-(a/b),那也就是说我们可以直接令a= y1-y2,b= x2-x1 (只要满足商为-k即可)。
此时F(x,y)=(y1-y2)x+(x2-x1)y+c=0,我们再随意带一个点进去(比如(x1,y1)),便可求得c= x1y2-x2y1,即得到该直线的方程为:
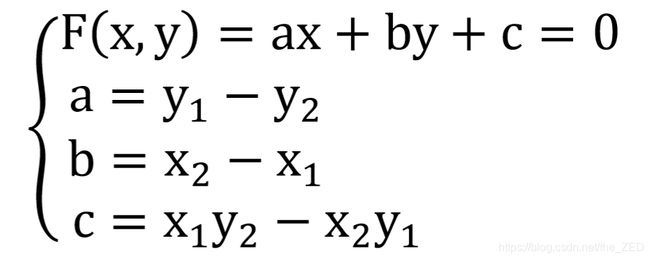
② 对于某个点(x,y),我们要知道其与直线方程F(x,y)存在如下关系:
F(x,y)=0,在直线上
F(x,y)>0,在直线上方
F(x,y)<0,在直线下方
因此,我们可以直接将中点M(xp+1,yp+0.5)带入直线方程中:
即d=F(xp+1, yp+0.5)=axp+1+byp+0.5+c,我们就可以根据d的值来确定下一个像素点:
d=0,选P2,P1均可,我们这里取P1
d>0,M在直线上方,故取P1为下一像素点
d<0,M在直线下方,故取P2为下一像素点
若设当前像素点为P(xp,yp),我们考虑d>=0和d<0两种情况:
d>=0,此时P1(xp+1,yp)为下一像素点,则再下一像素点为(xp+2,yp+0.5):
d’= F(xp+2,yp+0.5)=axp+2+byp+0.5+c=[axp+1+yp+0.5+c]+a=d+a
此时d’=d+a,增量为a
d<0,此时P2(xp+1,yp+1)为下一像素点,则再下一像素点为(xp+2,yp+1.5):
d’’= F(xp+2,yp+1.5)=axp+2+byp+1.5+c=[axp+1+yp+0.5+c]+a+b=d+a+b
此时d’’=d+a+b,增量为a+b
③ 注意到d0的初始化是用(x1,y0.5)来计算的:即d0=a+0.5b+c
且在后面的迭代中, y始终都含有0.5。而我们在迭代中判断下一个点纵坐标的取值时仅仅与d值的正负有关,因此为了摆脱浮点数的出现,我们统一将所有di的计算都使用2di来代替,因此d0=2a+b+2c,增量d’=2a,增量d’’=2a+2b
下面给出用matlab实现该算法的完整代码:
function main %测试代码
clc
clear;
Bresenham(0,0,50,40,'r')
function Bresenham(x1,y1,x2,y2,color) %Bresnham算法
a = (y1-y2);
b = (x2-x1);
c = x1*y2-x2*y1;
d=2*a+b+c;
d1=2*a;
d2=2*(a+b);
x=x1;
y=y1;
hold on
scatter(x,y,'.',color)
for i=x:x2
if d<0
x=x+1;
y=y+1;
d=d+d2;
else
x=x+1;
d=d+d1;
end
scatter(x,y,'.',color)
end
plot([x1,x2],[y1,y2]) %绘制原线以对比
grid minor
hold off
运行后得到的效果如下:
可以看出,中点算法在x轴上进行变化时,y上的取值严格按照Bresenham的原理进行取值。该算法作为数值微分法(DDA)的改进算法,其采用了直线的一般式方程、增量思想、实现整数加法等优化的思路,其成像的主要思想是以贴合直线为中心,使得这样的算法在绘制出的效果上是优于DDA算法的。