python实现反距离权重插值(IDW)
原文:https://mp.weixin.qq.com/s/2y13vGtqj55Fae-72YXY6g
1 什么叫反距离权重插值?
反距离权重:距离未知点最近的点分配的权重较大,且权重作为距离的函数而减小。
插值:利用已知点数据计算未知点数据,如下图所示:
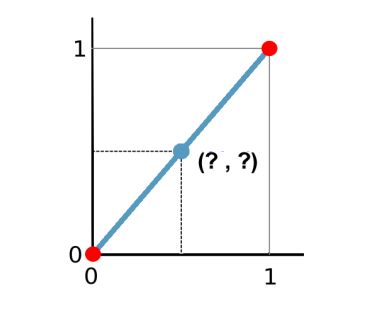
红色为已知点,蓝色为未知点,可通过线性插值得到。
近点的影响比远点的大,可通过设定固定的最近邻居个数来计算紫色未知点。
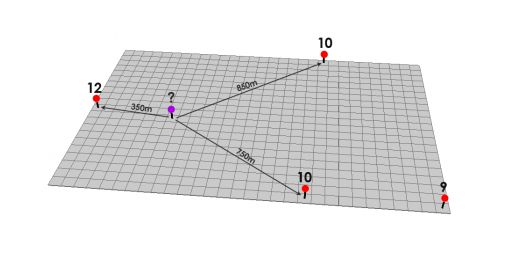
此外,还可通过设置查找半径的方式进行空间插值。
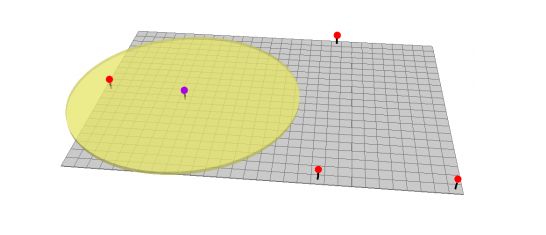
插值点是根据它们与已知像元值的距离来估计的。 更接近已知值的点将比更远的点受到更大的影响。 如果幂为1,则是平滑插值曲面。
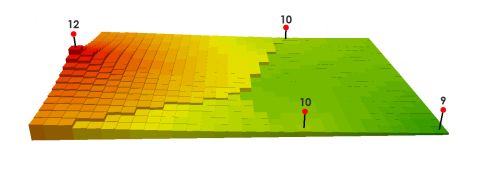
如果幂为2,峰值更加局部化,不像 1 那样平均。
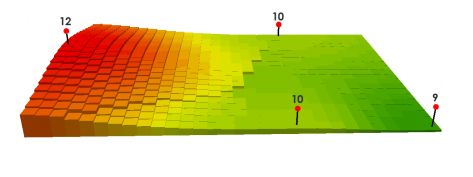
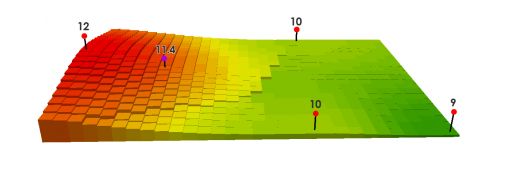
假设选定最近的3个邻居,邻居与紫色点的距离为:
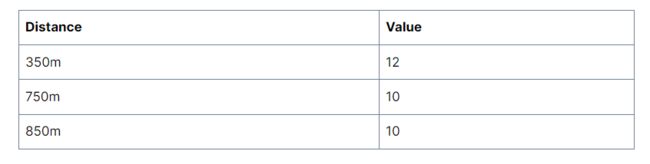
根据反距离权重的公式:
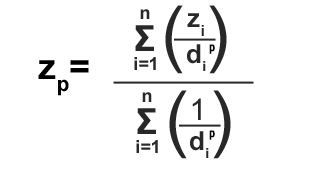
当幂为1时,得到紫色点的值为:
((12/350) + (10/750) + (10/850)) / ((1/350) + (1/750) + (1/850)) = 11.1
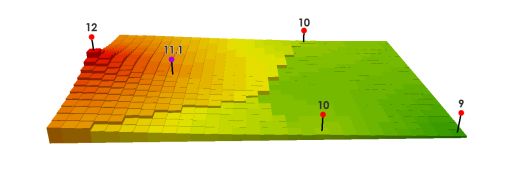
当幂为2时,得到紫色点的值为:
((12/350^2) + (10/750^2) + (10/850^2)) / ((1/350^2) + (1/750^2) + (1/850^2)) = 11.4
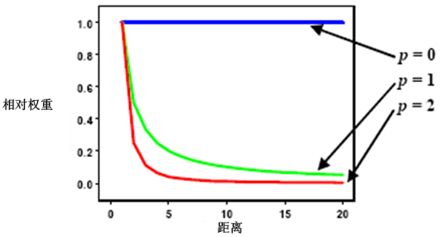
从公式中可以发现,权重与反距离(数据点与未知点之间)的p次幂成正比。随着距离的增加,权重将迅速降低。权重下降的速度取决于p值。
- 如果p=0,则表示权重不随距离减小,且因每个权重的值均相同,未知点的值将是搜索邻域内的所有数据值的平均值。
- 随着p值的增大,较远数据点的权重将迅速减小。
- 如果p值极大,则仅最邻近的数据点会对未知点产生影响。
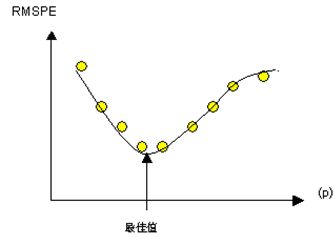
可通过最小化均方根预测误差(RMSPE)确定最佳幂值。RMSPE是在交叉验证过程中计算出的统计数据。将提供最小化均方根预测误差的幂为最佳幂。
2 python 实现
1) 使用scipy插值
原图与采样:

代码参考:https://github.com/mengjizhiyou/inverse_distance_weighting
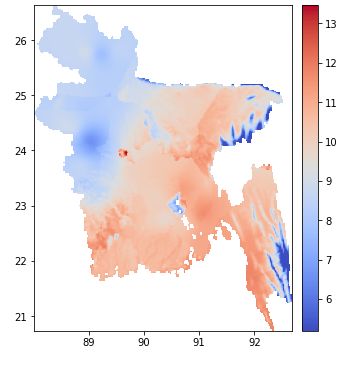
2) 使用pyidw插值
https://github.com/yahyatamim/pyidw
from pyidw import idw
idw.regression_idw_interpolation(
input_point_shapefile="Bangladesh_Temperature.shp",
input_raster_file="Bangladesh_Elevation.tif",
extent_shapefile="Bangladesh_Border.shp",
column_name="Min_Temp",
power=2,
polynomial_degree=1,
search_radious=5,
output_resolution=250,
)
参考:
https://gisgeography.com/inverse-distance-weighting-idw-interpolation/