深度学习进阶:自然语言处理入门:第1章 神经网络的复习
深度学习进阶:自然语言处理入门
- 第1章 神经网络的复习
-
- 1.1 数学和Python的复习
-
- 1.1.1 向量和矩阵
- 1.1.2 矩阵的对应元素的运算
- 1.1.3 广播
- 1.1.4 向量内积和矩阵乘积
- 1.1.5 矩阵的形状检查
- 1.2 神经网络的推理
-
- 1.2.1 神经网络的推理的全貌图
-
- 激活函数
- 输出层和激活函数 代码
- 1.2.2 层的类化及正向传播的实现
-
- 两层神经网络 (简单的只有正向传播,没有反向传播)
- 1.3 神经网络的学习
-
- 1.3.1 损失函数
-
- SoftmaxWithLoss类( )
- 1.3.2 导数和梯度
- 1.3.3 链式法则
- 1.3.4 计算图
-
- 1.3.4.1 乘法节点
- 1.3.4.2 分支节点
- 1.3.4.3 Repeat 节点
- 1.3.4.4 Sum 节点
- 1.3.4.5 MatMul 节点
-
- MatMul 类
- 1.3.5 梯度的推导和反向传播的实现
-
- 1.3.5.1 Sigmoid 层
- 1.3.5.2 Affine 层
- 1.3.5.3 Softmax with Loss 层
- 1.3.6 权重的更新
-
- SGD类
- 运行伪代码
- 1.4 使用神经网络解决问题
-
- 1.4.1 螺旋状数据集
- 1.4.2 神经网络的实现
- 1.4.3 学习用的代码
- 1.4.4 Trainer类
- 1.5 计算的高速化
-
- 1.5.1 位精度
- 1.5.2 GPU(CuPy)
- 1.6 小结
第1章 神经网络的复习
1.1 数学和Python的复习
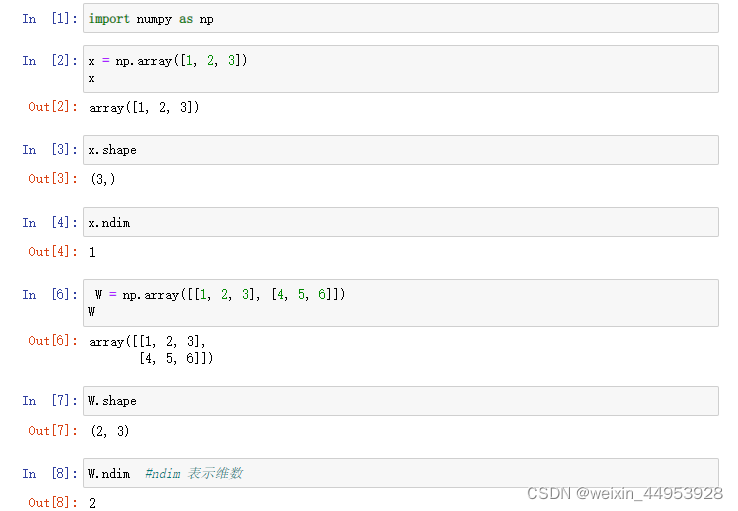
1.1.1 向量和矩阵
在数学和深度学习等许多领域,向量一般作为列向量处理。不过,考虑到实现层面的一致性,本书将向量作为行向量处理
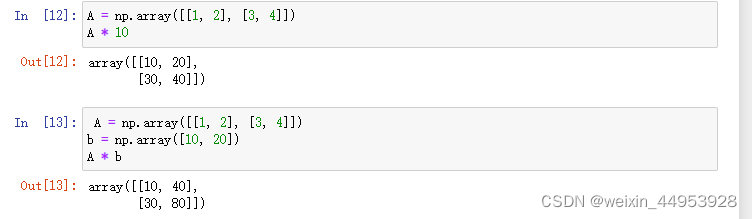
1.1.2 矩阵的对应元素的运算
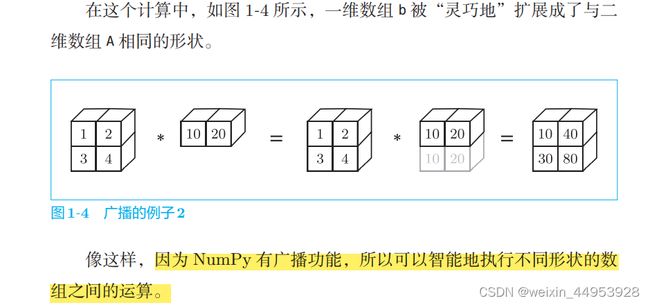
1.1.3 广播
1.1.4 向量内积和矩阵乘积
1.1.5 矩阵的形状检查
1.2 神经网络的推理
神经网络中进行的处理可以分为学习和推理两部分
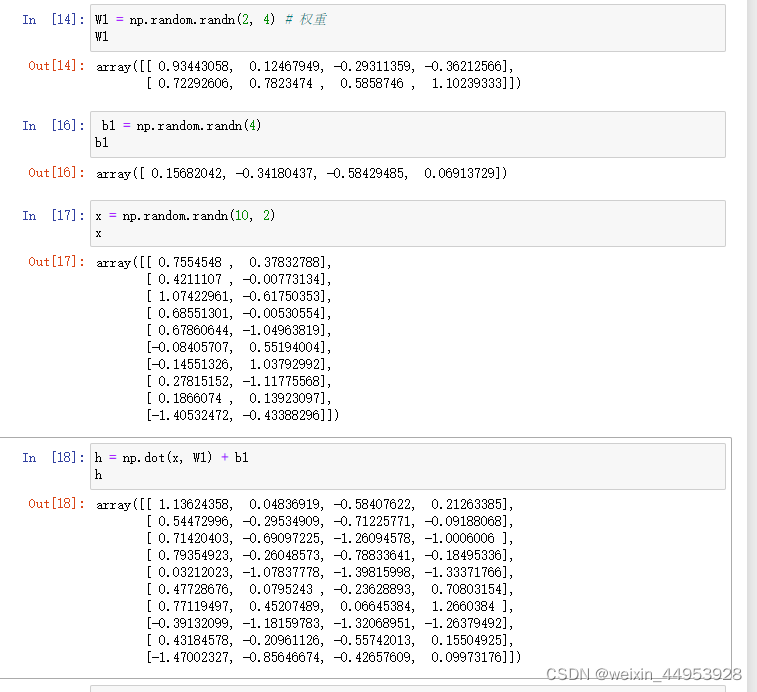
1.2.1 神经网络的推理的全貌图
import numpy as np
W1 = np.random.randn(2, 4) # 权重
b1 = np.random.randn(4) # 偏置
x = np.random.randn(10, 2) # 输入
h = np.dot(x, W1) + b1
激活函数
def sigmoid(x):
return 1 / (1 + np.exp(-x))
输出层和激活函数 代码
import numpy as np
def sigmoid(x):
return 1 / (1 + np.exp(-x))
x = np.random.randn(10, 2) #小批量10个
#输入
W1 = np.random.randn(2, 4)
b1 = np.random.randn(4)
#输出
W2 = np.random.randn(4, 3)
b2 = np.random.randn(3)
#隐藏层h和s一起是一层
h = np.dot(x, W1) + b1
a = sigmoid(h)
#输出层
s = np.dot(a, W2) + b2
1.2.2 层的类化及正向传播的实现
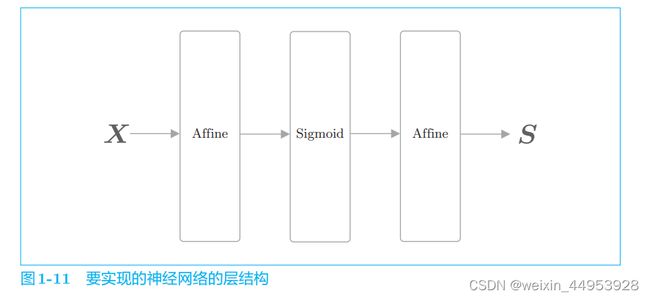
我们将神经网络进行的处理实现为层。这里将全连接层的变换实 现为 Affine 层,将 sigmoid 函数的变换实现为 Sigmoid 层。因为全连接层 的变换相当于几何学领域的仿射变换,所以称为 Affine 层。
神经网络的推理所进行的处理相当于神经网络的*正向传播.顾名思义, 正向传播是从输入层到输出层的传播。此时,构成神经网络的各层 从输入向输出方向按顺序传播处理结果.
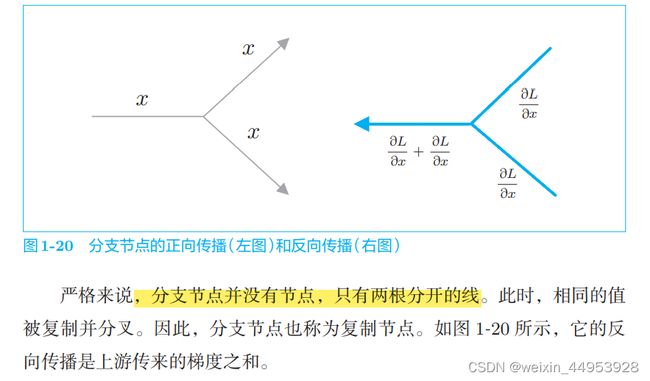
之后我们会进行神经网络的学习,那时会按与正向传播相反的顺序传播数据(梯度),所以称为反向传播。
本书在实现这些层时,制定以 下“代码规范”。 -
- **所有的层都有 forward() 方法和 backward() 方法 **
- 所有的层都有 params 和 grads 实例变量
首先,forward() 方法和 backward() 方法分别对应正向传播和反向传播。
params 使用列表保存权重和偏置等参 数(参数可能有多个,所以用列表保存)
grads 以与 params 中的参数对应 的形式,使用列表保存各个参数的梯度(后述)
两层神经网络 (简单的只有正向传播,没有反向传播)
import numpy as np
#激活函数 层
class Sigmoid:
def __init__(self):
self.params = []
def forward(self, x):
return 1 / (1 + np.exp(-x))
#全连接
class Affine:
def __init__(self, W, b):
self.params = [W, b]
def forward(self, x):
W, b = self.params
out = np.dot(x, W) + b
return out
class TwoLayerNet:
def __init__(self, input_size, hidden_size, output_size):
I, H, O = input_size, hidden_size, output_size
# 初始化权重和偏置
W1 = np.random.randn(I, H)
b1 = np.random.randn(H)
W2 = np.random.randn(H, O)
b2 = np.random.randn(O)
# 生成层
self.layers = [
Affine(W1, b1),
Sigmoid(),
Affine(W2, b2)
]
# 将所有的权重整理到列表中
self.params = []
for layer in self.layers:
self.params += layer.params
def predict(self, x):
for layer in self.layers:
x = layer.forward(x)
return x
x = np.random.randn(10, 2)
model = TwoLayerNet(2, 4, 3)
s = model.predict(x)
print(s)
1.3 神经网络的学习
1.3.1 损失函数
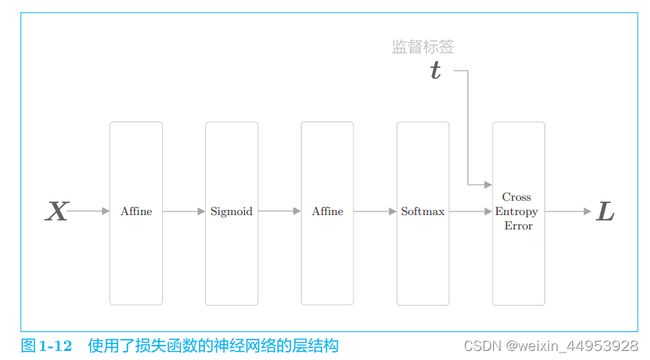
计算神经网络的损失要使用损失函数(loss function)。进行多类别分类的神经网络通常使用交叉熵误差(cross entropy error)作为损失函数。 此时,交叉熵误差由神经网络输出的各类别的概率和监督标签求得。
SoftmaxWithLoss类( )
def cross_entropy_error(y, t):
if y.ndim == 1:
t = t.reshape(1, t.size)
y = y.reshape(1, y.size)
# 在监督标签为one-hot-vector的情况下,转换为正确解标签的索引
if t.size == y.size:
t = t.argmax(axis=1)
batch_size = y.shape[0]
return -np.sum(np.log(y[np.arange(batch_size), t] + 1e-7)) / batch_size
class SoftmaxWithLoss:
def __init__(self):
self.params, self.grads = [], []
self.y = None # softmax的输出
self.t = None # 监督标签
def forward(self, x, t):
self.t = t
self.y = softmax(x)
# 在监督标签为one-hot向量的情况下,转换为正确解标签的索引
if self.t.size == self.y.size:
self.t = self.t.argmax(axis=1)
loss = cross_entropy_error(self.y, self.t)
return loss
def backward(self, dout=1):
batch_size = self.t.shape[0]
dx = self.y.copy()
dx[np.arange(batch_size), self.t] -= 1
dx *= dout
dx = dx / batch_size
return dx
1.3.2 导数和梯度
神经网络的学习的目标是找到损失尽可能小的参数。
本书使用的“梯度”一词与数学中的“梯度”是不同的。 数学中的梯度仅限于关于向量的导数。而在深度学习领域,一般 也会定义关于矩阵和张量的导数,称为“梯度”。
1.3.3 链式法则
那么,神经网络的梯度怎么求呢?这就轮到 **误差反向传播法 **出场了。
理解误差反向传播法的关键是链式法则。链式法则是复合函数的求导法 则,其中复合函数是由多个函数构成的函数
1.3.4 计算图
梯度沿与正向传播相反的方向传播,这个反方向的传播 称为反向传播
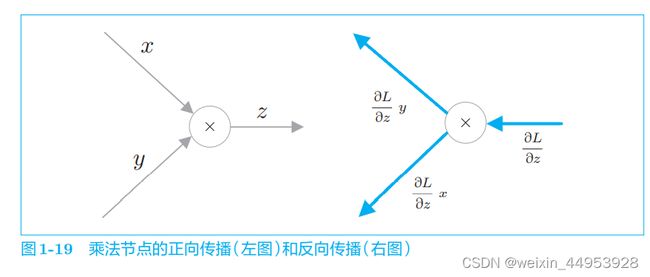
1.3.4.1 乘法节点
1.3.4.2 分支节点
1.3.4.3 Repeat 节点
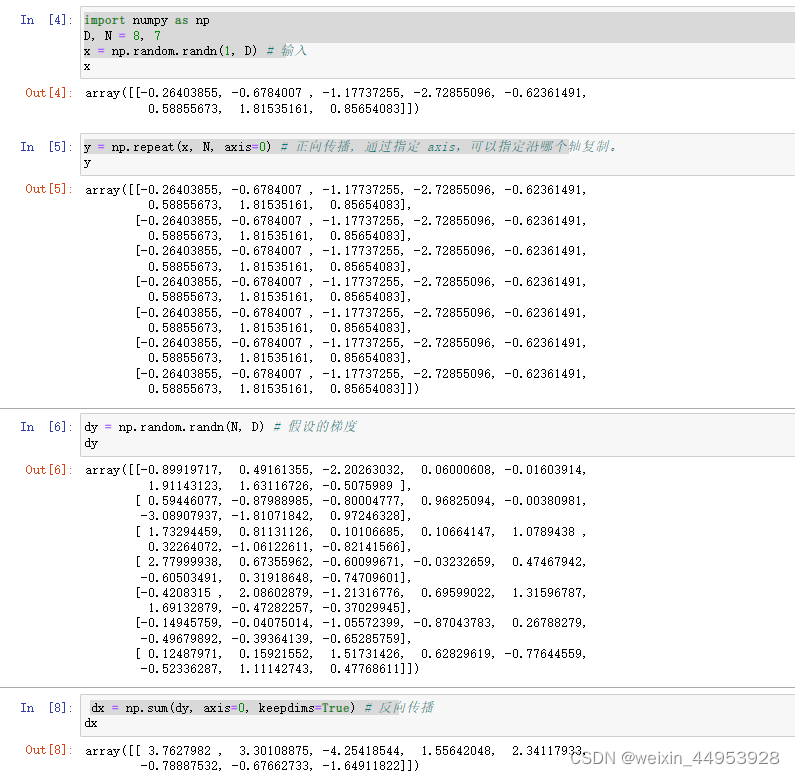
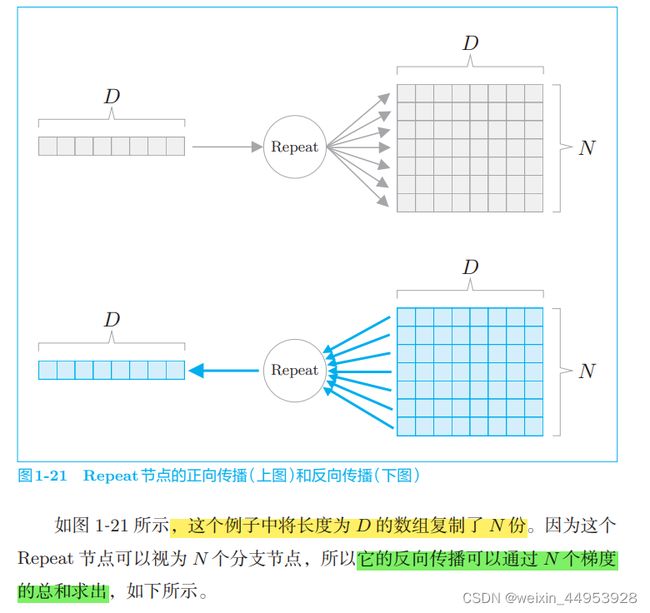
分支节点有两个分支,但也可以扩展为 N 个分支(副本),这里称为 Repeat 节点。
import numpy as np
D, N = 8, 7
x = np.random.randn(1, D) # 输入
#通过 np.repeat() 方法进行元素的复制。上面的例子中将复制 N 次 数组 x。通过指定 axis,可以指定沿哪个轴复制。
y = np.repeat(x, N, axis=0) # 正向传播, 通过指定 axis,可以指定沿哪个轴复制。
dy = np.random.randn(N, D) # 假设的梯度
dx = np.sum(dy, axis=0, keepdims=True) # 反向传播,keepdims=True,可以维持二维数组的维数。
因为反向传播时要计算 总和,所以使用 NumPy 的 sum() 方法。
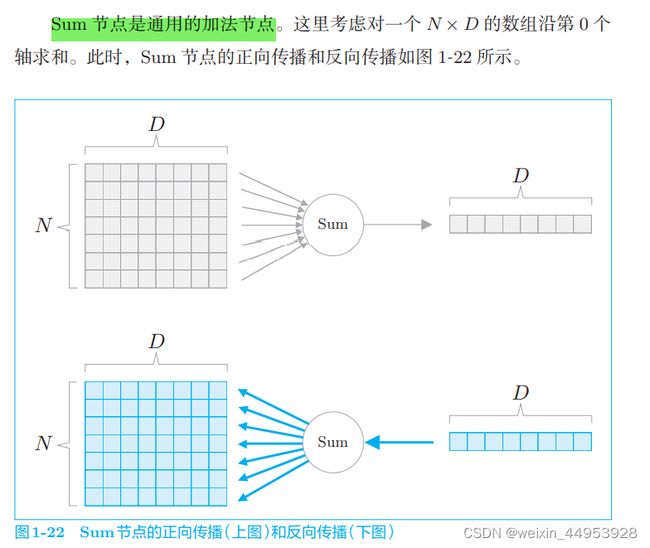
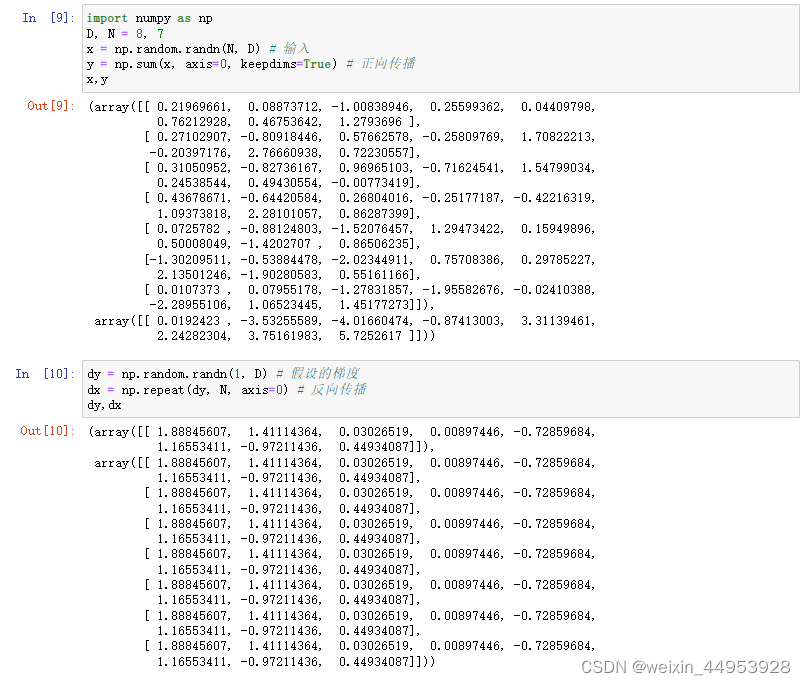
1.3.4.4 Sum 节点
如上所示,Sum 节点的正向传播通过 np.sum() 方法实现,反向传播通 过 np.repeat() 方法实现。有趣的是,Sum 节点和 Repeat 节点存在逆向关 系。所谓逆向关系,是指 Sum 节点的正向传播相当于 Repeat 节点的反向传 播,Sum 节点的反向传播相当于 Repeat 节点的正向传播。
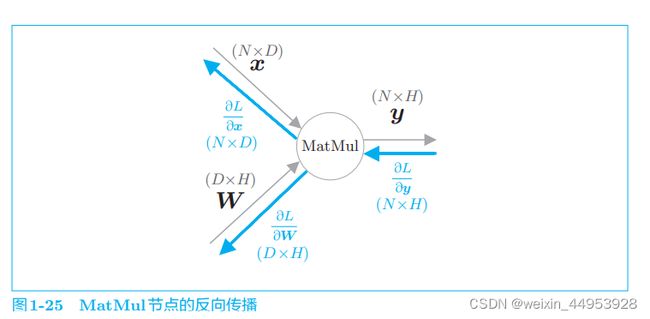
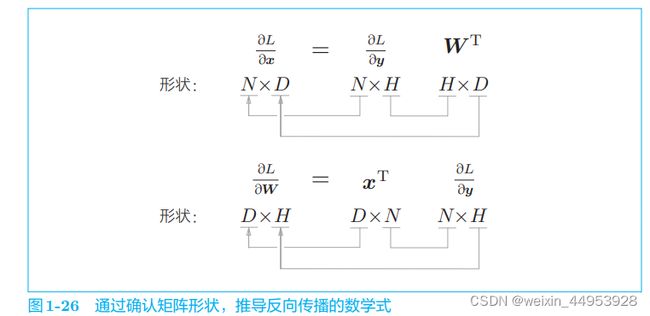
1.3.4.5 MatMul 节点
MatMul 类
class MatMul:
def __init__(self, W):
self.params = [W]
self.grads = [np.zeros_like(W)]
self.x = None
def forward(self, x):
W, = self.params
out = np.dot(x, W)
self.x = x
return out
def backward(self, dout):
W, = self.params
dx = np.dot(dout, W.T)
dW = np.dot(self.x.T, dout)
self.grads[0][...] = dW
return dx
MatMul 层在params 中保存要学习的参数。另外,以与其对应的形式将梯度保存在 grads 中。在反向传播时求 dx 和 dw,并在实例变量 grads 中设置权重的梯度
在设置梯度的值时,像grads[0] […]=dW 这样,使用了省略号。由此,可以固定 NumPy 数组的内存地址,覆盖 NumPy 数组的元素。
和省略号一样,这里也可以进行基于grads[0] = dW 的赋值。不 同的是,在使用省略号的情况下会覆盖掉NumPy数组。这是浅复制(shallow copy)和深复制(deep copy)的差异。grads[0] = dW 的赋值相当于浅复制,grads[0] […]=dW 的覆盖相当于深复制。

的地址是固定的)。通过固定这个内存地址,实例变量 grads 的处理会变简单
在 grads 列表中保存各个参数的梯度。此时,grads 列表中的各个 元素是 NumPy 数组,仅在生成层时生成一次。然后,使用省略号, 在不改变 NumPy 数组的内存地址的情况下覆盖数据。这样一来, 将梯度汇总在一起的工作就只需要在开始时进行一次即可。
1.3.5 梯度的推导和反向传播的实现
这里,我们将实现 Sigmoid 层、全连接层 Affine 层和 Softmax with Loss 层。
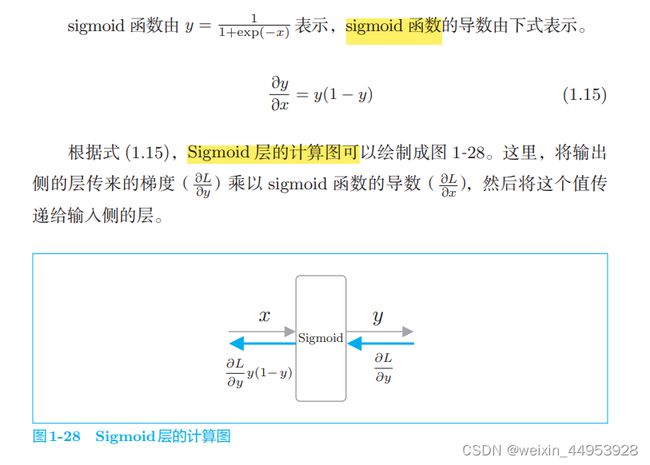
1.3.5.1 Sigmoid 层
class Sigmoid:
def __init__(self):
self.params, self.grads = [], []
self.out = None
def forward(self, x):
out = 1 / (1 + np.exp(-x))
self.out = out
return out
def backward(self, dout):
dx = dout * (1.0 - self.out) * self.out
return dx
这里将正向传播的输出保存在实例变量 out 中。然后,在反向传播中, 使用这个 out 变量进行计算。
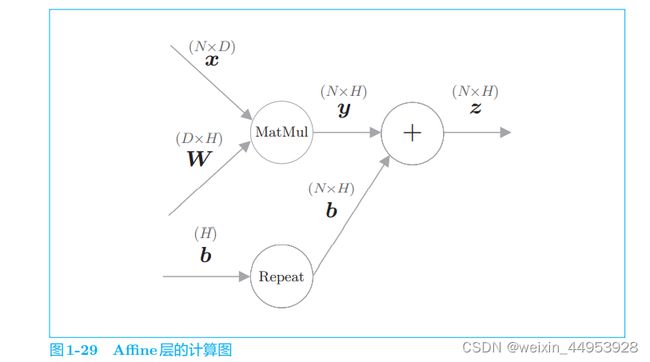
1.3.5.2 Affine 层
如前所示,我们通过 y = np.dot(x, W) + b 实现了 Affine 层的正向传播。
class Affine:
def __init__(self, W, b):
self.params = [W, b]
self.grads = [np.zeros_like(W), np.zeros_like(b)]
self.x = None
def forward(self, x):
W, b = self.params
out = np.dot(x, W) + b
self.x = x
return out
def backward(self, dout):
W, b = self.params
dx = np.dot(dout, W.T)
dW = np.dot(self.x.T, dout)
db = np.sum(dout, axis=0)
self.grads[0][...] = dW
self.grads[1][...] = db
return dx
Affine 层将参数保存在实例变量 params 中,将 梯度保存在实例变量 grads 中。它的反向传播可以通过执行 MatMul 节点和 Repeat 节点的反向传播来实现。Repeat 节点的反向传播可以通过 np.sum() 计算出来,此时注意矩阵的形状,就可以清楚地知道应该对哪个轴(axis) 求和。最后,将权重参数的梯度设置给实例变量 grads。以上就是 Affine 层 的实现
使用已经实现的 MatMul 层,可以更轻松地实现 Affine 层。这里 出于复习的目的,没有使用 MatMul 层,而是使用 NumPy 的方 法进行了实现。
1.3.5.3 Softmax with Loss 层
def softmax(x):
if x.ndim == 2:
x = x - x.max(axis=1, keepdims=True)
x = np.exp(x)
x /= x.sum(axis=1, keepdims=True)
elif x.ndim == 1:
x = x - np.max(x)
x = np.exp(x) / np.sum(np.exp(x))
return x
def cross_entropy_error(y, t):
if y.ndim == 1:
t = t.reshape(1, t.size)
y = y.reshape(1, y.size)
# 在监督标签为one-hot-vector的情况下,转换为正确解标签的索引
if t.size == y.size:
t = t.argmax(axis=1)
batch_size = y.shape[0]
return -np.sum(np.log(y[np.arange(batch_size), t] + 1e-7)) / batch_size
class SoftmaxWithLoss:
def __init__(self):
self.params, self.grads = [], []
self.y = None # softmax的输出
self.t = None # 监督标签
def forward(self, x, t):
self.t = t
self.y = softmax(x)
# 在监督标签为one-hot向量的情况下,转换为正确解标签的索引
if self.t.size == self.y.size:
self.t = self.t.argmax(axis=1)
loss = cross_entropy_error(self.y, self.t)
return loss
def backward(self, dout=1):
batch_size = self.t.shape[0]
dx = self.y.copy()
dx[np.arange(batch_size), self.t] -= 1
dx *= dout
dx = dx / batch_size
return dx
1.3.6 权重的更新
-
**步骤 1:mini-batch **
从训练数据中随机选出多笔数据。
-
步骤 2:计算梯度
基于误差反向传播法,计算损失函数关于各个权重参数的梯度
-
步骤 3:更新参数
使用梯度更新权重参数。
-
步骤 4:重复
根据需要重复多次步骤 1、步骤 2 和步骤 3。
通过将参数向该梯度的反方向更新, 可以降低损失。这就是梯度下降法(gradient descent)。之后,根据需要将 这一操作重复多次即可。
在上面的步骤 3 中更新权重。权重更新方法有很多,这里我们来 实现其中最简单的随机梯度下降法(Stochastic Gradient Descent,SGD)。 其中,“随机”是指使用随机选择的数据(mini-batch)的梯度。
SGD类
class SGD:
'''
随机梯度下降法(Stochastic Gradient Descent)
'''
def __init__(self, lr=0.01):
self.lr = lr
def update(self, params, grads):
for i in range(len(params)):
params[i] -= self.lr * grads[i]
运行伪代码
model = TwoLayerNet(...)
optimizer = SGD()
for i in range(10000):
...
x_batch, t_batch = get_mini_batch(...) # 获取mini-batch
loss = model.forward(x_batch, t_batch)
model.backward()
optimizer.update(model.params, model.grads)
...
1.4 使用神经网络解决问题
本书在 dataset 目录中提供了几个便于处理数据集的类
1.4.1 螺旋状数据集
ys.path.append('..') # 为了引入父目录的文件而进行的设定,将父目录添加到了 import 的检索路
径中。
读取螺旋(旋涡)状数据 的类,其用法如下所示
略(以后读懂了,在补充)
1.4.2 神经网络的实现
我们来实现一个具有一个隐藏层的神经网络。首先,import 语句 和初始化程序的 init() 如下所示
import sys
sys.path.append('..') # 为了引入父目录的文件而进行的设定
import numpy as np
from common.layers import Affine, Sigmoid, SoftmaxWithLoss
class TwoLayerNet:
def __init__(self, input_size, hidden_size, output_size):
I, H, O = input_size, hidden_size, output_size
# 初始化权重和偏置
W1 = 0.01 * np.random.randn(I, H)
b1 = np.zeros(H)
W2 = 0.01 * np.random.randn(H, O)
b2 = np.zeros(O)
# 生成层
self.layers = [
Affine(W1, b1),
Sigmoid(),
Affine(W2, b2)
]
self.loss_layer = SoftmaxWithLoss()
# 将所有的权重和偏置整理到列表中
self.params, self.grads = [], []
for layer in self.layers:
self.params += layer.params
self.grads += layer.grads
def predict(self, x):
for layer in self.layers:
x = layer.forward(x)
return x
def forward(self, x, t):
score = self.predict(x)
loss = self.loss_layer.forward(score, t)
return loss
def backward(self, dout=1):
dout = self.loss_layer.backward(dout)
for layer in reversed(self.layers):
dout = layer.backward(dout)
return dout
初始化程序接收 3 个参数。input_size 是输入层的神经元数,hidden_ size 是隐藏层的神经元数,output_size 是输出层的神经元数。
在内部实 现中,首先用零向量(np.zeros())初始化偏置,再用小的随机数(0.01 * np.random.randn())初始化权重。通过将权重设成小的随机数,学习可以更 容易地进行。
接着,生成必要的层,并将它们整理到实例变量 layers 列表 中。最后,将这个模型使用到的参数和梯度归纳在一起。
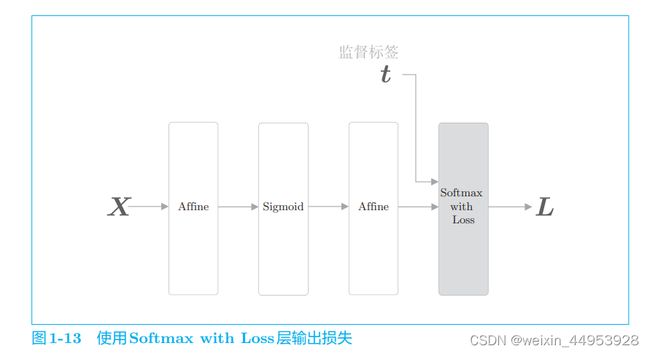
因为 Softmax with Loss 层和其他层的处理方式不同,所以不将 它放入 layers列表中,而是单独存储在实例变量 loss_layer中。
接着,我们为 TwoLayerNet 实现 3 个方法,即进行推理的 predict() 方 法、正向传播的 forward() 方法和反向传播的 backward() 方法
1.4.3 学习用的代码
import sys
sys.path.append('..') # 为了引入父目录的文件而进行的设定
import numpy as np
from common.optimizer import SGD
from dataset import spiral
import matplotlib.pyplot as plt
from two_layer_net import TwoLayerNet
# 设定超参数
#就是设定学习的 epoch数、mini-batch 的大小、隐藏层的神经元数和学习率。
max_epoch = 300 #训练次数
batch_size = 30 #mini-batch 的大小
hidden_size = 10 #隐藏层的神经元数
learning_rate = 1.0 #学习率
# 进行数据的读入,生成神经网络(模型)和优化器
x, t = spiral.load_data() #使用 spiral.load_data() 进行数据的读入。此时,x 是输入数据,t 是监督标签。
model = TwoLayerNet(input_size=2, hidden_size=hidden_size, output_size=3)
optimizer = SGD(lr=learning_rate)
# 学习用的变量
data_size = len(x)
max_iters = data_size // batch_size
total_loss = 0
loss_count = 0
loss_list = []
for epoch in range(max_epoch):
# 打乱数据
idx = np.random.permutation(data_size) #以随机打乱数据的索引。
x = x[idx]
t = t[idx]
for iters in range(max_iters):
batch_x = x[iters*batch_size:(iters+1)*batch_size]
batch_t = t[iters*batch_size:(iters+1)*batch_size]
#4 计算梯度,更新参数
loss = model.forward(batch_x, batch_t)
model.backward()
optimizer.update(model.params, model.grads)
total_loss += loss
loss_count += 1
#5 定期输出学习过程
#每 10 次迭代计算 1 次平均损失,并将其添加到变量 loss_list 中
if (iters+1) % 10 == 0:
avg_loss = total_loss / loss_count
print('| epoch %d | iter %d / %d | loss %.2f' % (epoch + 1, iters + 1, max_iters, avg_loss))
loss_list.append(avg_loss)
total_loss, loss_count = 0, 0
# 绘制学习结果
plt.plot(np.arange(len(loss_list)), loss_list, label='train')
plt.xlabel('iterations (x10)')
plt.ylabel('loss')
plt.show()
# 绘制决策边界
h = 0.001
x_min, x_max = x[:, 0].min() - .1, x[:, 0].max() + .1
y_min, y_max = x[:, 1].min() - .1, x[:, 1].max() + .1
xx, yy = np.meshgrid(np.arange(x_min, x_max, h), np.arange(y_min, y_max, h))
X = np.c_[xx.ravel(), yy.ravel()]
score = model.predict(X)
predict_cls = np.argmax(score, axis=1)
Z = predict_cls.reshape(xx.shape)
plt.contourf(xx, yy, Z)
plt.axis('off')
# 绘制数据点
x, t = spiral.load_data()
N = 100
CLS_NUM = 3
markers = ['o', 'x', '^']
for i in range(CLS_NUM):
plt.scatter(x[i*N:(i+1)*N, 0], x[i*N:(i+1)*N, 1], s=40, marker=markers[i])
plt.show()
在进行学习时,需要随机选择数据作为 mini-batch。这里,我们以epoch 为单位打乱数据,对于打乱后的数据,按顺序从头开始抽取数据。数 据的打乱(准确地说,是数据索引的打乱)使用 np.random.permutation() 方 法。给定参数 N,该方法可以返回 0 到 N − 1 的随机序列,其实际的使用 示例如下所示。
>>> import numpy as np
>>> np.random.permutation(10)
array([7, 6, 8, 3, 5, 0, 4, 1, 9, 2])
>>> np.random.permutation(10)
array([1, 5, 7, 3, 9, 2, 8, 6, 0, 4])
1.4.4 Trainer类
如前所述,本书中有很多机会执行神经网络的学习。为此,就需要编写 前面那样的学习用的代码。然而,每次都写相同的代码太无聊了,因此我们 将进行学习的类作为 Trainer 类提供出来。Trainer 类的内部实现和刚才的源 代码几乎相同,只是添加了一些新的功能而已,我们在需要的时候再详细说 明其用法。

import sys
sys.path.append('..') # 为了引入父目录的文件而进行的设定
from common.optimizer import SGD
from common.trainer import Trainer
from dataset import spiral
from two_layer_net import TwoLayerNet
# 设定超参数
max_epoch = 300
batch_size = 30
hidden_size = 10
learning_rate = 1.0
x, t = spiral.load_data()
model = TwoLayerNet(input_size=2, hidden_size=hidden_size, output_size=3)
optimizer = SGD(lr=learning_rate)
trainer = Trainer(model, optimizer)
trainer.fit(x, t, max_epoch, batch_size, eval_interval=10)
trainer.plot()
1.5 计算的高速化
神经网络的学习和推理需要大量的计算。
本节将简单介绍一下可以有效加速神经网络的计算的位 精度和 GPU 的相关内容
1.5.1 位精度
NumPy 的浮点数默认使用 64 位的数据类型。
>>> import numpy as np
>>> a = np.random.randn(3)
>>> a.dtype
dtype('float64')
通过 NumPy 数组的实例变量 dtype,可以查看数据类型。上面的结果 是 float64,表示 64 位的浮点数
NumPy 中默认使用 64 位浮点数。但是,我们已经知道使用 32 位浮点数也可以无损地(识别精度几乎不下降)进行神经网络的推理和学习。
再者,就计算速度而言,32 位 浮点数也能更高速地进行计算(浮点数的计算速度依赖于 CPU 或 GPU 的 架构)。
因此,本书优先使用 32 位浮点数。要在 NumPy 中使用 32 位浮点数, 可以像下面这样将数据类型指定为 np.float32 或者 ‘f’。
>>> b = np.random.randn(3).astype(np.float32)
>>> b.dtype
dtype('float32')
>>> c = np.random.randn(3).astype('f')
>>> c.dtype
dtype('float32')
另外,我们已经知道,如果只是神经网络的推理,则即使使用 16 位浮 点数进行计算,精度也基本上不会下降.不过,虽然 NumPy 中准备有16 位浮点数,但是普通 CPU 或 GPU 中的运算是用 32 位执行的。因此, 即便变换为 16 位浮点数,因为计算本身还是用 32 位浮点数执行的,所以处 理速度方面并不能获得什么好处
1.5.2 GPU(CuPy)
深度学习的计算由大量的乘法累加运算组成。这些乘法累加运算的绝大 部分可以并行计算,这是 GPU 比 CPU 擅长的地方。因此,一般的深度学 习框架都被设计为既可以在 CPU 上运行,也可以在 GPU 上运行。
本书中可以选用 Python 库 CuPy[3]。CuPy 是基于 GPU 进行并行计 算的库。要使用 CuPy,需要使用安装有 NVIDIA 的 GPU 的机器,并且需 要安装 CUDA 这个面向 GPU 的通用并行计算平台。详细的安装方法请参 考 CuPy 的官方安装文档 。
使用 Cupy,可以轻松地使用 NVIDIA 的 GPU 进行并行计算。更重要 的是,CuPy 和 NumPy 拥有共同的 API。下面我们来看一个简单的使用 示例。
>>> import cupy as cp
>>> x = cp.arange(6).reshape(2, 3).astype('f')
>>> x
array([[ 0., 1., 2.],
[ 3., 4., 5.]], dtype=float32)
>>> x.sum(axis=1)
array([ 3., 12.], dtype=float32
1.6 小结
- 神经网络具有输入层、隐藏层和输出层
- 通过全连接层进行线性变换,通过激活函数进行非线性变换
- 全连接层和 mini-batch 处理都可以写成矩阵计算
- 使用误差反向传播法可以高效地求解神经网络的损失的梯度
- 使用计算图能够将神经网络中发生的处理可视化,这有助于理解正向传播和反向传播
- 在神经网络的实现中,通过将组件模块化为层,可以简化实现
- 数据的位精度和 GPU 并行计算对神经网络的高速化非常重要