逻辑回归算法
1、逻辑回归理论
逻辑回归也被称为广义线性回归模型,它与线性回归模型的形式基本上相同,都具有 theta * xb,其中theta是待求参数,其区别在于他们的因变量不同,多重线性回归直接将 theta * xb作为因变量,即y = theta * xb,而logistic回归则通过函数S将 theta * xb对应到一个隐状态p,p = S( theta * xb),然后根据p与1-p的大小决定因变量的值。通常使用Sigmoid函数
sigmoid函数
1/ (1 + np.exp(-t))
当t趋近+∞,sigmoid趋近1,
当t趋近-∞,sigmoid趋近0,
当t趋近0,sigmoid趋近0.5

即如果真实值y为1,预测值p(也是下图中的x)越小,损失函数-log(x)越大,如果真实值y为0,预测值p越大,损失函数-log(1-x)越大
这个损失函数没有公式解,只能使用梯度下降法求解,该损失函数是一个凸函数,没有局部最优解,只有一个全局最优解。
损失函数的梯度具体推导过程跳过。
最终损失函数的梯度为:
2、代码实现逻辑回归
编写LogisticRegression.py文件
import numpy as np
from common.metrics import accuracy_score
class LogisticRegression:
def __init__(self):
# 系数coefficient θ1到θn,是一个向量
self.coef_ = None
# 截距 θ0,是一个数值
self.interception_ = None
self._theta = None
def _sigmoid(self, t):
return 1./(1. + np.exp(-t))
def fit(self, X_train, y_train, eta=0.01, n_iters=1e4, epsilon=1e-8):
# 原函数
def J(theta, X_b, y):
y_hat = self._sigmoid(X_b.dot(theta))
return -np.sum(y * np.log(y_hat) + (1 - y) * np.log(1 - y_hat))/len(X_b)
# 导函数
def dJ(theta, X_b, y):
return X_b.T.dot(self._sigmoid(X_b.dot(theta)) - y) / len(X_b)
def gradient_descent(X_b, y, theta_init, eta, n_iters=1e4, epsilon=1e-8):
theta = theta_init
i_iter = 1
while i_iter < n_iters:
# 当前点的导数值
gradient = dJ(theta, X_b, y)
last_theta = theta
# 自变量的变化量 * 当前点的导数值 = 损失函数的变化量
# 导数的正负值代表损失函数在当前点的变化趋势是增大还是减小,因此如果导数为负则theta增加,损失函数趋于变小
# 如果导数为正,则theta减小,损失函数趋于变小,因此theta减去导数值,损失函数趋于变小
# 在eta合适的情况下,随着循环进行,导数值逐渐趋近0,eta是常数,损失函数的变化量会越来越小
theta = theta - eta * gradient
# abs求绝对值
if (abs(J(theta, X_b, y) - J(last_theta, X_b, y)) < epsilon):
break
i_iter += 1
return theta
X_b = np.hstack([np.ones((len(X_train), 1)), X_train])
theta_init = np.zeros(X_b.shape[1])
self._theta = gradient_descent(X_b=X_b, y=y_train, theta_init=theta_init, eta=eta, n_iters=n_iters, epsilon=epsilon)
self.interception_ = self._theta[0]
self.coef_ = self._theta[1:]
return self
# 预测结果的概率
def predict_proba(self, X_predict):
X_b = np.hstack([np.ones((len(X_predict), 1)), X_predict])
return self._sigmoid(X_b.dot(self._theta))
def predict(self, X_predict):
proba = self.predict_proba(X_predict)
return np.array(proba >= 0.5, dtype=int)
def score(self, X_test, y_test):
y_predict = self.predict(X_test)
return accuracy_score(y_test, y_predict)
测试:
import numpy as np
from sklearn import datasets
import matplotlib.pyplot as plt
from sklearn.model_selection import train_test_split
from common.LogisticRegression import LogisticRegression
iris = datasets.load_iris()
X = iris.data
y = iris.target
X = X[y<2,:2]
y = y[y<2]
X_train,X_test,y_train,y_test = train_test_split(X, y, random_state=666)
log_reg = LogisticRegression()
log_reg.fit(X_train, y_train)
print(log_reg.score(X_test, y_test))
print(log_reg.predict_proba(X_test))
3、决策边界
代码实现绘制决策边界:
import numpy as np
from sklearn import datasets
import matplotlib.pyplot as plt
from sklearn.model_selection import train_test_split
from common.LogisticRegression import LogisticRegression
iris = datasets.load_iris()
X = iris.data
y = iris.target
X = X[y<2,:2]
y = y[y<2]
X_train,X_test,y_train,y_test = train_test_split(X, y, random_state=666)
log_reg = LogisticRegression()
log_reg.fit(X_train, y_train)
print(log_reg.score(X_test, y_test))
print(log_reg.predict_proba(X_test))
def x2(x1):
return (-log_reg.interception_ - log_reg.coef_[0] * x1) / log_reg.coef_[1]
x1_plot = np.linspace(4,8,1000)
x2_plot = x2(x1_plot)
# y==0筛选行,0筛选第0个特征
# plt.scatter(X[y==0,0], X[y==0,1],color='r')
# plt.scatter(X[y==1,0], X[y==1,1],color='b')
# plt.plot(x1_plot,x2_plot)
# plt.show()
plt.scatter(X_test[y_test==0,0], X_test[y_test==0,1],color='r')
plt.scatter(X_test[y_test==1,0], X_test[y_test==1,1],color='b')
plt.plot(x1_plot,x2_plot)
plt.show()
4、逻辑回归中使用多项式特征
4.1 自定义逻辑回归+多项式项
通过引入多项式项使模型能够预测非线性分布的数据,自定义PolynomialLogisticRegression.py文件:
from sklearn.preprocessing import StandardScaler
from sklearn.preprocessing import PolynomialFeatures
from common.LogisticRegression import LogisticRegression
from sklearn.pipeline import Pipeline
def PolynomialLogisticRegression(degree):
return Pipeline([
('poly', PolynomialFeatures(degree=degree)),
('std_standar', StandardScaler()),
('log_reg', LogisticRegression())
])
测试:
import numpy as np
import matplotlib.pyplot as plt
from common.LogisticRegression import LogisticRegression
from common.PolynomialLogisticRegression import PolynomialLogisticRegression
np.random.seed(666)
X = np.random.normal(0, 1, size=[100, 2])
y = np.array(X[:,0] ** 2 + X[:,1] ** 2 > 1.5, dtype=int)
# plt.scatter(X[y==0,0],X[y==0,1],color='r')
# plt.scatter(X[y==1,0],X[y==1,1],color='b')
# plt.show()
# 使用线性模型逻辑回归预测
log_reg = LogisticRegression()
log_reg.fit(X,y)
print(log_reg.score(X,y))
# 添加多项式项预测
poly_log_reg = PolynomialLogisticRegression(degree=2)
poly_log_reg.fit(X, y)
print(poly_log_reg.score(X, y))
# degree=20时发生了过拟合,需要进行模型正则化
poly_log_reg = PolynomialLogisticRegression(degree=20)
poly_log_reg.fit(X, y)
print(poly_log_reg.score(X, y))
4.2 使用scikitlearn中的逻辑回归+多项式项
编写SKPolynomialLogisticRegression.py文件
from sklearn.preprocessing import StandardScaler
from sklearn.preprocessing import PolynomialFeatures
from sklearn.linear_model import LogisticRegression
from sklearn.pipeline import Pipeline
def SKPolynomialLogisticRegression(degree,C=1,penalty='l2'):
return Pipeline([
('poly', PolynomialFeatures(degree=degree)),
('std_standar', StandardScaler()),
# ‘newton-cg’,‘sag’和‘lbfgs’等solvers仅支持‘L2’regularization,
# ‘liblinear’ solver同时支持‘L1’、‘L2’regularization,若dual=Ture,则仅支持L2 penalty。
# 决定惩罚项选择的有2个参数:dual和solver,如果要选L1范数,dual必须是False,solver必须是liblinear
#
# solver默认值lbfgs,默认会报错:
# Solver lbfgs supports only 'l2' or 'none' penalties, got l1 penalty.
('log_reg', LogisticRegression(C=C,penalty=penalty,solver='liblinear'))
])
使用scikitlearn中的逻辑回归测试:
import numpy as np
import matplotlib.pyplot as plt
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LogisticRegression
from common.SKPolynomialLogisticRegression import SKPolynomialLogisticRegression
np.random.seed(666)
X = np.random.normal(0, 1, size=(200,2))
y = np.array(X[:,0] ** 2 + X[:,1] > 1.5, dtype=int)
for i in range(20):
y[np.random.randint(200)] = 1
# plt.scatter(X[y==0,0],X[y==0,1])
# plt.scatter(X[y==1,0],X[y==1,1])
# plt.show()
# 使用sklearn中的线性逻辑回归预测
X_train,X_test,y_train,y_test = train_test_split(X, y)
log_reg = LogisticRegression()
print(log_reg.fit(X_train, y_train))
print(log_reg.score(X_train,y_train))
print(log_reg.score(X_test,y_test))
print("=======================================")
# 使用sklearn添加多项式项预测,默认模型正则化的系数C=1
sk_log_reg = SKPolynomialLogisticRegression(degree=2)
sk_log_reg.fit(X_train, y_train)
print(sk_log_reg.score(X_train,y_train))
print(sk_log_reg.score(X_test,y_test))
# degree=20时模型出现过拟合,模型的泛化能力变差
sk_log_reg = SKPolynomialLogisticRegression(degree=20)
sk_log_reg.fit(X_train, y_train)
print(sk_log_reg.score(X_train,y_train))
print(sk_log_reg.score(X_test,y_test))
# c=0.1,放大模型正则化后损失函数中theta的占比,设置c=0.1后,比默认的c=1模型泛化能力好
sk_log_reg = SKPolynomialLogisticRegression(degree=20,C=0.1)
sk_log_reg.fit(X_train, y_train)
print(sk_log_reg.score(X_train,y_train))
print(sk_log_reg.score(X_test,y_test))
# penalty='l1'模型正则化使用L1正则化
sk_log_reg = SKPolynomialLogisticRegression(degree=20,C=0.1,penalty='l1')
sk_log_reg.fit(X_train, y_train)
print(sk_log_reg.score(X_train,y_train))
print(sk_log_reg.score(X_test,y_test))
5、OVR与OVO
逻辑回归只可以解决二分类问题,几乎所有二分类算法都可以使用以下两种方式改造为解决多分类问题:
- OVR
- OVO
5.1 OVR
一对剩余的意思是当要对n种类别的样本进行分类时,分别取一种样本作为一类,将剩余的所有类型的样本看做另一类,这样就形成了n个二分类问题。
5.2 OVO
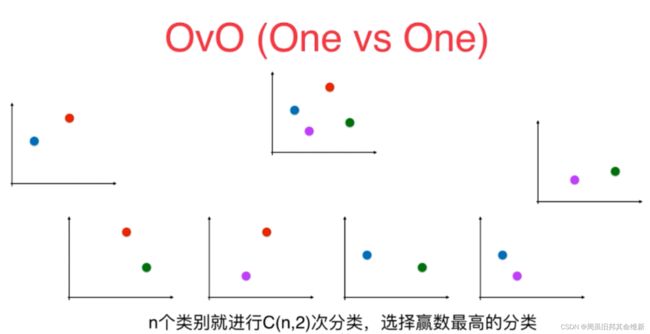
使用二分类算法来解决多分类问题的一种策略。从字面意思可以看出它的核心思想就是一对一。所谓的“一”,指的是类别。而“对”指的是从训练集中划分不同的两个类别的组合来训练出多个分类器。
在预测阶段,只需要将测试样本分别扔给训练阶段训练好的3个分类器进行预测,最后将3个分类器预测出的结果进行投票统计,票数最高的结果为预测结果。
虽然OVO的计算复杂度更高,但预测结果也比OVR更高。
OVR与OVO代码实现:
import numpy as np
import matplotlib.pyplot as plt
from sklearn import datasets
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LogisticRegression
from sklearn.multiclass import OneVsRestClassifier
from sklearn.multiclass import OneVsOneClassifier
iris = datasets.load_iris()
X = iris.data
y = iris.target
# multi_class:默认auto(如果二分类或者求解器为liblinear时,则为OVR,否则为multinomial)
X_train,X_test,y_train,y_test = train_test_split(X, y, random_state=666)
log_reg = LogisticRegression()
print(str(log_reg.fit(X_train,y_train)))
print(log_reg.score(X_test, y_test))
# ovo的方式
X_train,X_test,y_train,y_test = train_test_split(X, y, random_state=666)
log_reg2 = LogisticRegression(multi_class='multinomial',solver='newton-cg')
print(str(log_reg2.fit(X_train,y_train)))
print(log_reg2.score(X_test, y_test))
print('======================================')
ovr = OneVsRestClassifier(estimator=log_reg)
ovr.fit(X_train,y_train)
print(ovr.score(X_test,y_test))
ovo = OneVsOneClassifier(estimator=log_reg)
ovo.fit(X_train,y_train)
print(ovo.score(X_test,y_test))


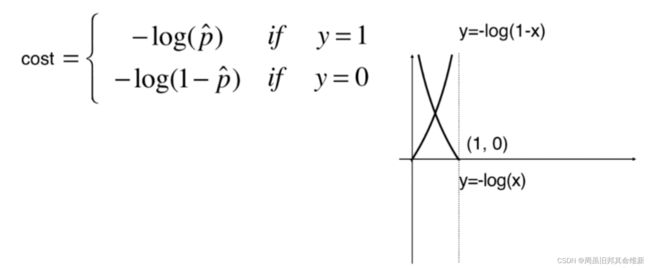
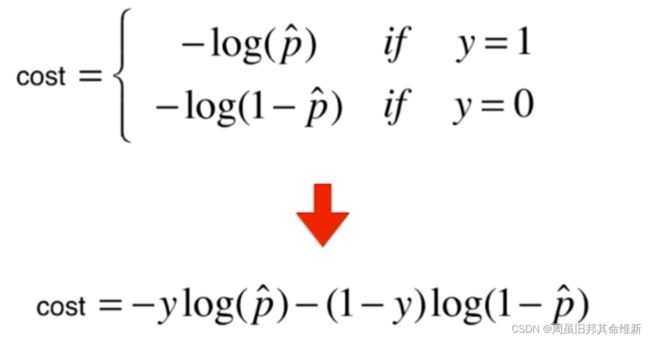

![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-vMNMjkj5-1667568328794)(C:\Users\11244\AppData\Roaming\Typora\typora-user-images\image-20221103105951455.png)]](http://img.e-com-net.com/image/info8/775c5a3a67d64a4daa53224d2d1680c4.jpg)