读sklearn源码学机器学习——kmeans聚类算法

题记：凌晨3点半的不眠，是这个时代太聒噪，还是内心的不安

kmeans知识体系

从代码中梳理知识体系

sklearn中kmeans源码

源码结构

kmeans算法属于cluster包的k_means.py文件。使用的过程中通过

from sklearn.cluster import Kmeans导入

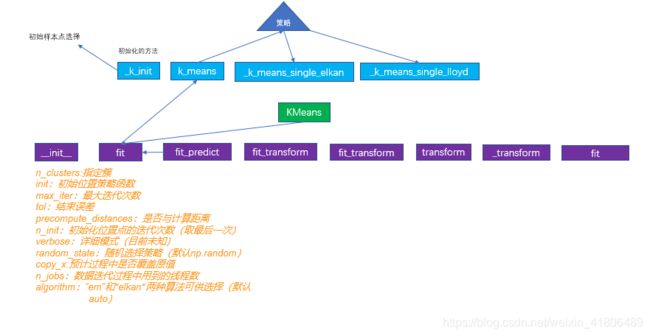
在使用常规（不含大批量数据的情况下）kmeans算法的实现过程如上图所示，Kmeans主类，包含若干的内部函数（紫色所示），若干的外部函数（蓝色所示）。函数之间的调用关系如上面箭头所示。最核心的函数有：_k_init函数，提供算法的初始化信息，这个过程中牵扯到策略的选择；_kmeans_single_elkan，通过elkan策略的中心点选择；_kmeans_single_lloyd，通过EM策略的中心点选择。

kmeans关键点

1.初始聚类中心点的选择
2.聚类策略的选取（EM,elkn还是其他…）
3.聚类距离的计算
优缺点：
喜欢这个背景加英文。

The k-means problem is solved using either Lloyd's or Elkan's algorithm.

    The average complexity is given by O(k n T), were n is the number of
    samples and T is the number of iteration.

    The worst case complexity is given by O(n^(k+2/p)) with
    n = n_samples, p = n_features. (D. Arthur and S. Vassilvitskii,
    'How slow is the k-means method?' SoCG2006)

    In practice, the k-means algorithm is very fast (one of the fastest
    clustering algorithms available), but it falls in local minima. That's why
    it can be useful to restart it several times.

    If the algorithm stops before fully converging (because of ``tol`` or
    ``max_iter``), ``labels_`` and ``cluster_centers_`` will not be consistent,
    i.e. the ``cluster_centers_`` will not be the means of the points in each
    cluster. Also, the estimator will reassign ``labels_`` after the last
    iteration to make ``labels_`` consistent with ``predict`` on the training
    set.

解释：kmeans算法通过Lloyd 或 Elkan算法实现。lloyd也就是我们手的em算法，elkan算法引入三角形两边之和大于第三边的定理减少没必要的欧式距离计算，但是这种算法类似动态规划，你需要开辟额外的存储空间。
kmeans算法的平均算法复杂度为O（knt）, 其中k是聚类个数，n是样本个数，t是最大迭代次数。最坏情况的算法复杂度O（n^(k+2/p)）。kmeans算法的运算速度很快，最快的聚类算法之一了。但是在问题非凸的时候容易陷入局部最优解。

逐一回答

1、挑个简单的，距离的计算
可以发现在参数的设置过程中，以及运算过程中多次用到了样本之间距离的运算，距离的运算一般有以下几种。
闵可夫斯基距离（Minkowski distance）

当p=2,就是我们常用的
欧式距离（euclidean distance）

当p=1,
曼哈顿距离、城市街区距离（Manhattan distance,city block distance）

VDM距离

理解：

样本间距离计算技巧

阅读源码中我发现，sklearn中的kmeans算法用的时欧氏距离，而且在样本间距离计算的时候直接用的矩阵进行计算，在一般情况下我们对于两个样本间距离的计算恐怕是这样：
比如我们想计算第一个样本与其他样本之间的距离，代码如下。

def normal():
    X=np.asmatrix([[1,2,3],[4,5,6],[7,8,9]])
    normalRes=[]
    for item in X:
        tolerent=X[np.newaxis, 0]-item[np.newaxis, 0]
        normalRes.append(np.einsum("ij,ij",tolerent,tolerent))
    normalDistance=np.sqrt(normalRes)
    return normalDistance

但是在源码中距离的计算实现逻辑是这样的：

def rowNorms(X):#对行每个元素取平方加和
    return np.einsum("ij,ij->i",X,X)
def newMethod(x,y):

    xx=rowNorms(x)[:,np.newaxis]
    yy=rowNorms(y)[np.newaxis,:]
    dot=np.dot(x,y.T)

    print(xx)
    print(yy)
    print(dot)
    res = xx + yy - 2 * dot
    return np.sqrt(res)
X=np.asmatrix([[1,2,3],[4,5,6],[7,8,9]])
print(newMethod(X[[0,1]],X))

运行结果：

[[ 0.          5.19615242 10.39230485]]

刚开始我觉得这样有点多次依据吧~然而很快发现了自己太年轻，比如我想实现第一个跟第二个样本，跟剩下样本的距离就可以：

print(newMethod(X[[0,1]],X))
[[ 0.          5.19615242 10.39230485]
 [ 5.19615242  0.          5.19615242]]

简直不能太方便，而且这种计算方法，直接矩阵操作，在时间和空间复杂度上都是非常好的。接下来附上推导过程：
参考：https://blog.csdn.net/IT_forlearn/article/details/100022244

这个方法用着是真的香
(凌晨4点钟，去睡觉，后面继续更新).

kmeans算法原理

在周志华的《机器学习》中对于kmeans算法的工作过程是这样描述的

将以上过程用程序化的语言进行描述如下所示：
kmeans算法的实施过程
1、确定聚类中心（策略自己定义）
2、进行若干次的循环（循环次数自己定义）：
2.1将剩下的样本根据距离划入相应的簇中
2.2计算新的簇中心
2.3如果新簇与老簇达到了结束条件（即两个分类中心之间的距离偏移量），就提前退出
3、输出结果

kmeans算法实现

将上面的过程通过python实现，整个的逻辑过程，代码如下(代码中relativeDist,squaredNornal涉及到距离计算的优化和f范数的计算可以参阅我的其他博客)：

    n_cluster=3
    maxItem=300
    tol=1e-4#停止条件，即center的改变的误差平方和
    matrix_data=np.asarray(pd.read_csv("yourData.csv",header=None))
    # 1初始化,先用随机初始化
    n_samples,n_feature=matrix_data.shape
    seed=np.random.permutation(n_samples)[:n_cluster]
    center=matrix_data[seed]
    for i in range(maxItem):
        relative_distance=relativeDist(matrix_data,center)
        labels=np.argmin(relative_distance,axis=1)
        #计算聚类中心
        new_center=np.zeros((n_cluster,n_feature))
        num_center=np.zeros(n_cluster)
        for r,v in enumerate(labels):
            new_center[v]+=matrix_data[r]
            num_center[v]+=1
        #out不开辟新的临时变量
        np.maximum(num_center,1,out=num_center)#防止除0
        np.reciprocal(num_center,dtype=float,out=num_center)#取倒数
        np.einsum("ij,i->ij",new_center,num_center.T,out=new_center)#求取center
        # 用f范数评价
        center_shift_total=squaredNornal(center-new_center)
        if squaredNornal(center_shift_total<tol):
            break
        center=copy.deepcopy(new_center)

kmeans算法改进

通过上文的分析不难发现，kmeans算法的性能主要依靠两个方面：
1、初始位置的确定。一个好的初始位置将直接影响后续后续的迭代次数以及聚类的好坏。
2、距离的计算。整个kmeans算法的运行过程就是样本与聚类中心点的距离计算过程，所以在距离计算上计算方法的改进也直接影响聚类的效果。
以上两点的改进过程，可以查阅我的其他博客。