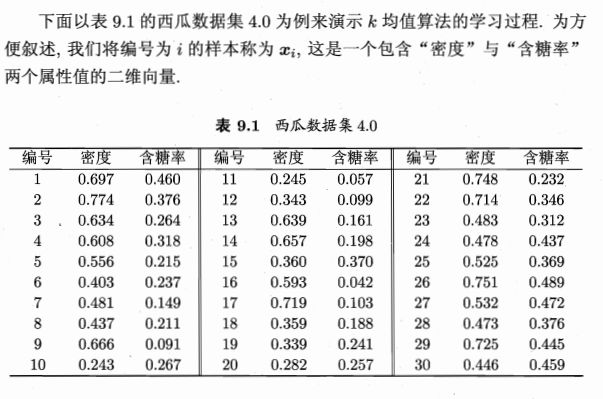
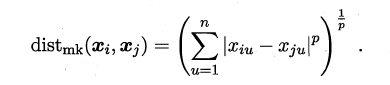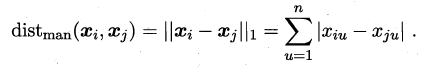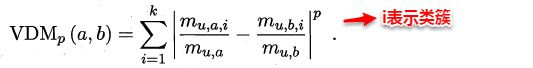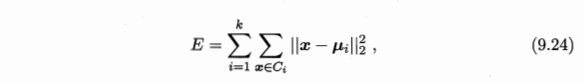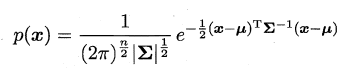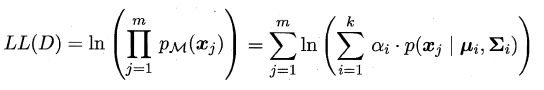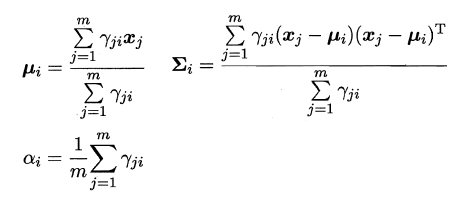【周志华机器学习】九、聚类

参考资料

1. Machine-learning-learning-notes
2. LeeML-Notes
3. ML-NLP

本博客是根据周志华的西瓜书和参考资料1、2、3所做的笔记，主要用于学习，非技术类博客，因此存在大量复制粘贴，请见谅。
如果本篇博客有后记部分，则该部分表示的是在书本原有的基础知识上，进行的知识点的扩充。

代码演示见于github仓库

1. 基本概念

聚类是一种经典的无监督学习方法，无监督学习的目标是通过对无标记训练样本的学习，发掘和揭示数据集本身潜在的结构与规律，即不依赖于训练数据集的类标记信息。聚类则是试图将数据集的样本划分为若干个互不相交的类簇，从而每个簇对应一个潜在的类别。

聚类直观上来说是将相似的样本聚在一起，从而形成一个类簇（cluster）。

那首先的问题是如何来度量相似性（similarity measure）呢？这便是距离度量，在生活中我们说差别小则相似，对应到多维样本，每个样本可以对应于高维空间中的一个数据点，若它们的距离相近，我们便可以称它们相似。

那接着如何来评价聚类结果的好坏呢？这便是性能度量，性能度量为评价聚类结果的好坏提供了一系列有效性指标。

1.1 距离度量

谈及距离度量，最熟悉的莫过于欧式距离了：即对应属性之间相减的平方和再开根号。度量距离还有其它的很多经典方法，通常它们需要满足一些基本性质：

最常用的距离度量方法是“闵可夫斯基距离”（Minkowski distance)：

当p=1时，闵可夫斯基距离即曼哈顿距离（Manhattan distance）：

当p=2时，闵可夫斯基距离即欧氏距离（Euclidean distance）：

我们知道属性分为两种：连续属性和离散属性（有限个取值）。对于连续值的属性，一般都可以被学习器所用，有时会根据具体的情形作相应的预处理，例如：归一化等；而对于离散值的属性，需要作下面进一步的处理：

• 若属性值之间存在序关系，则可以将其转化为连续值，例如：身高属性“高”“中等”“矮”，可转化为{1, 0.5, 0}。
• 若属性值之间不存在序关系，则通常将其转化为向量的形式，例如：性别属性“男”“女”，可转化为{（1,0），（0,1）}。

在进行距离度量时，易知连续属性和存在序关系的离散属性都可以直接参与计算，因为它们都可以反映一种程度，我们称其为“有序属性”；

而对于不存在序关系的离散属性，我们称其为：“无序属性”，显然无序属性再使用闵可夫斯基距离就行不通了。

对于无序属性，我们一般采用VDM(Value Difference Metric)进行距离的计算，例如：对于离散属性的两个取值a和b，定义：

于是，在计算两个样本之间的距离时，我们可以将闵可夫斯基距离和VDM混合在一起进行计算：

若我们定义的距离计算方法是用来度量相似性，例如下面将要讨论的聚类问题，即距离越小，相似性越大，反之距离越大，相似性越小。这时距离的度量方法并不一定需要满足前面所说的四个基本性质，这样的方法称为：非度量距离（non-metric distance）。

1.2 性能度量

由于聚类算法不依赖于样本的真实类标，就不能像监督学习的分类那般，通过计算分对分错（即精确度或错误率）来评价学习器的好坏或作为学习过程中的优化目标。一般聚类有两类性能度量指标：外部指标和内部指标。

1.2.1 外部指标

即将聚类结果与某个参考模型的结果进行比较，以参考模型的输出作为标准，来评价聚类好坏。假设聚类给出的结果为λ，参考模型给出的结果是λ*，则我们将样本进行两两配对，定义：

其中集合SS包含了在$C$中隶属于相同簇且在$C^{\ast }$中也隶属于相同簇的样本对,集合SD包含了在$C$中隶属于相同簇但在$C^{\ast }$中隶属于不同簇的样本对,……由于每个样本对$(c_i,a_j)(i<j)$仅能出现在一个集合中,因此有$a+b+c+d=m(m-1)/2$成立.

显然a和b代表着聚类结果好坏的正能量，b和c则表示参考结果和聚类结果相矛盾，基于这四个值可以导出以下常用的外部评价指标：

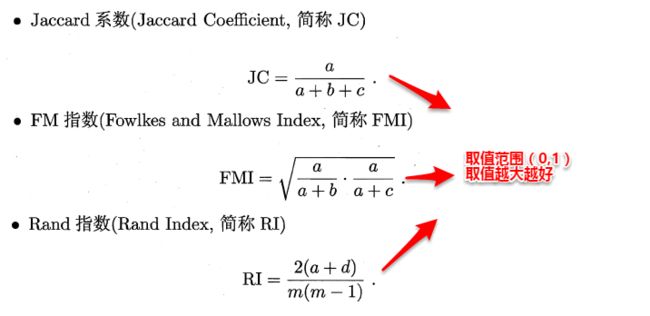
显然,上述性能度量的结果值均在$[0,1]$区间,值越大越好.

1.2.2 内部指标

内部指标即不依赖任何外部模型，直接对聚类的结果进行评估，聚类的目的是想将那些相似的样本尽可能聚在一起，不相似的样本尽可能分开。

对数据集$D=[D_1,D_2,...,D_m]$,假定通过聚类给出的簇划分为$C=[C_1,C_2,...,C_k]$,参考模型给出的簇划分为$C^{\ast }=[C_1^{\ast },C_2^{\ast },...,C_s^{\ast }]$.相应地,令$\lambda$与${\lambda }^{\ast }$分别表示与$C$和$C^{\ast }$对应的簇标记向量,我们将样本两两配对考虑,定义：

基于上面的四个距离，可以导出下面这些常用的内部评价指标：

2. 原型聚类

原型聚类即“基于原型的聚类”（prototype-based clustering），原型表示模板的意思，就是通过参考一个模板向量或模板分布的方式来完成聚类的过程，常见的K-Means便是基于簇中心来实现聚类，混合高斯聚类则是基于簇分布来实现聚类。

2.1 K-Means

K-Means的思想十分简单，首先随机指定类中心，根据样本与类中心的远近划分类簇，接着重新计算类中心，迭代直至收敛。但是其中迭代的过程并不是主观地想象得出，事实上，若将样本的类别看作“隐变量”（latent variable），类中心看作样本的分布参数，这一过程正是通过EM算法的两步走策略而计算出，其根本的目的是为了最小化平方误差函数E：

给定样本集$D=[D_1,D_2,...,D_m]$, "k均值”(k-means)算法针对聚类所得簇划分$C=[C_1,C_2,...,C_k]$最小化上述平方误差，其中${\mu }_i=\frac{1}{|C_i|}{\sum }_{x\in C_i}x$是簇$C_i$的均值向量.直观来看,式(9.24)在一定程度上刻画了簇内样本围绕簇均值向量的紧密程度,E值越小则簇内样本相似度越高。

算法流程如下：

更新当前均值向量后，不断重复上述过程，直到结果不再更新，迭代停止，算法停止，得到最终的簇划分。

1. k值的选择

在运行 K-均值算法的之前，我们首先要随机初始化所有的聚类中心点，下面介绍怎样做：

1. 聚类中心点的个数要小于所有训练集实例的数量。
2. 随机选择个训练实例，然后令个聚类中心分别与这个训练实例相等K-均值的一个问题在于，它有可能会停留在一个局部最小值处，而这取决于初始化的情况。

为了解决这个问题，我们通常需要多次运行 K-均值算法，每一次都重新进行随机初始化，最后再比较多次运行 K-均值的结果，选择代价函数最小的结果。这种方法在较小的时候（2-10）还是可行的，但是如果较大，这么做也可能不会有明显地改善。

没有所谓最好的选择聚类数的方法，通常是需要根据不同的问题，人工进行选择的。选择的时候思考我们运用 K-均值算法聚类的动机是什么。有一个可能会谈及的方法叫作肘部法则。关 于“肘部法则”，我们所需要做的是改变值，也就是聚类类别数目的总数。我们用一个聚类来运行 K 均值聚类方法。这就意味着，所有的数据都会分到一个聚类里，然后计算成本函数或者计算畸变函数。代表聚类数字。

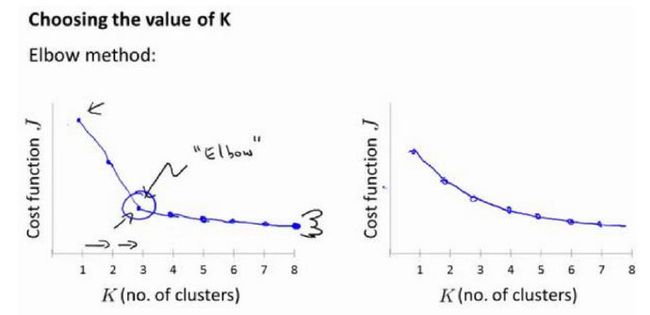
我们可能会得到一条类似于这样的曲线。像一个人的肘部。这就是“肘部法则”所做的，看起来就好像有一个很清楚的肘在那儿。从 1 到 2，从 2 到 3 之后，你会在 3 的时候达到一个肘点。在此之后，畸变值就下降的非常慢，看起来就像使用 3 个聚类来进行聚类是正确的，这是因为那个点是曲线的肘点，畸变值下降得很快， = 3之后就下降得很慢，那么我们就选 = 3。当你应用“肘部法则”的时候，如果你得到了一个像上面这样的图，那么这将是一种用来选择聚类个数的合理方法。

2. K-Means优缺点及改进

k-means：在大数据的条件下，会耗费大量的时间和内存。

优化k-means的建议：

• 减少聚类的数目K。因为，每个样本都要跟类中心计算距离。

• 减少样本的特征维度。比如说，通过PCA等进行降维。

• 考察其他的聚类算法，通过选取toy数据，去测试不同聚类算法的性能。

• hadoop集群，K-means算法是很容易进行并行计算的。

• 算法可能找到局部最优的聚类，而不是全局最优的聚类。使用改进的二分k-means算法。
  二分k-means算法：首先将整个数据集看成一个簇，然后进行一次k-means（k=2）算法将该簇一分为二，并计算每个簇的误差平方和，选择平方和最大的簇迭代上述过程再次一分为二，直至簇数达到用户指定的k为止，此时可以达到的全局最优。

2.2 学习向量量化（LVQ）

与k均值算法类似, “学习向量量化” (Learning Vector Quantization,简称LVQ)也是试图找到一组原型向量来刻画聚类结构,但与一般聚类算法不同的是,LVQ假设数据样本带有类别标记,学习过程利用样本的这些监督信息来辅助聚类。

首先LVQ根据样本的类标记，从各类中分别随机选出一个样本作为该类簇的原型，从而组成了一个原型特征向量组，接着从样本集中随机挑选一个样本，计算其与原型向量组中每个向量的距离，并选取距离最小的原型向量所在的类簇作为它的划分结果，再与真实类标比较。

若划分结果正确，则对应原型向量向这个样本靠近一些
若划分结果不正确，则对应原型向量向这个样本远离一些

讲$p_5$更新为$p^{\prime }$后，不断重复上述过程。

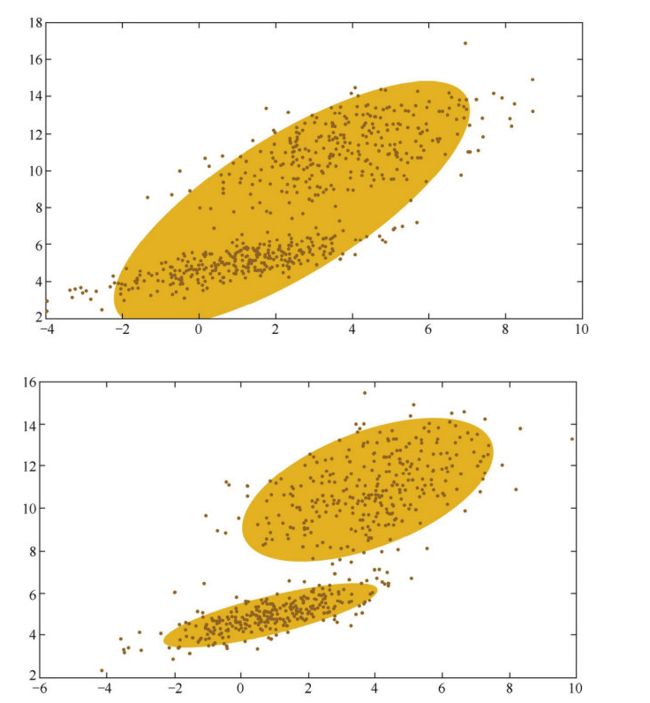
2.3 高斯混合聚类（GMM）

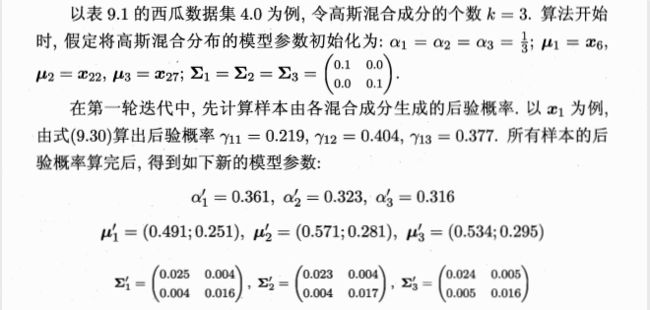
现在可以看出K-Means与LVQ都试图以类中心作为原型指导聚类，高斯混合聚类（Gaussian Mixed Model，GMM）则采用高斯分布来描述原型。现假设每个类簇中的样本都服从一个多维高斯分布，那么空间中的样本可以看作由k个多维高斯分布混合而成。

对于多维高斯分布，其概率密度函数如下所示：

其中u表示均值向量，∑表示协方差矩阵，可以看出一个多维高斯分布完全由这两个参数所确定。接着定义高斯混合分布为：

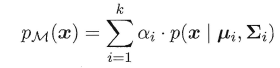
α称为混合系数${\sum }_{i=1}^k{\alpha }_i=1$，这样空间中样本的采集过程则可以抽象为：（1）先选择一个类簇（高斯分布），（2）再根据对应高斯分布的密度函数进行采样

此时只需要选择$P_M$最大时的类簇并将该样本划分到其中，看到这里很容易发现：这和贝叶斯分类不是神似吗，都是通过贝叶斯公式展开，然后计算类先验概率和类条件概率。但遗憾的是：这里没有真实类标信息，对于类条件概率，并不能像贝叶斯分类那样通过最大似然法美好地计算出来，因为这里的样本可能属于所有的类簇，这里的似然函数变为：

可以看出：简单的最大似然法根本无法求出所有的参数，这样$P_M$也就没法计算。但是可以通过使用EM算法进行迭代优化求解，首先对高斯分布的参数及混合系数进行随机初始化，计算出各个$P_M$（即${\gamma }_{ji}$，第i个样本属于j类），再最大化似然函数（即LL（D）分别对α、u和∑求偏导 ），对参数进行迭代更新。

高斯混合聚类的算法流程如下图所示：

不断重复上述过程。

GMM与K-Means相比

高斯混合模型与K均值算法的相同点是：

• 它们都是可用于聚类的算法；
• 都需要 指定K值；
• 都是使用EM算法来求解；
• 都往往只能收敛于局部最优。

而它相比于K 均值算法的优点是，可以给出一个样本属于某类的概率是多少；不仅仅可以用于聚类，还可以用于概率密度的估计；并且可以用于生成新的样本点。

3. 密度聚类

密度聚类则是基于密度的聚类（density-based clustering），它从样本分布的角度来考察样本之间的可连接性，并基于可连接性（密度可达）不断拓展疆域（类簇）。其中最著名的便是DBSCAN算法。

首先定义以下概念：

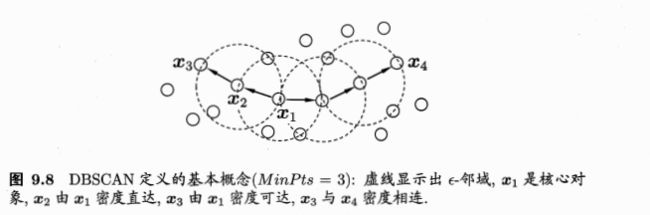
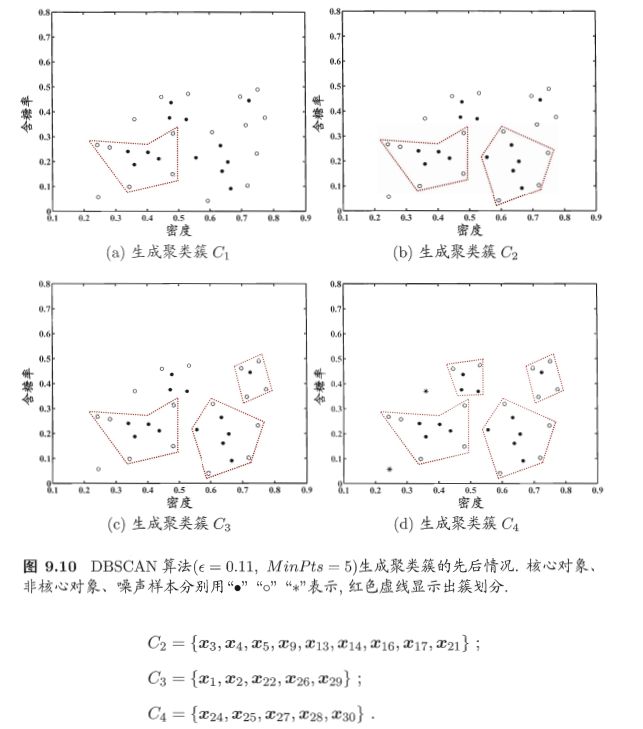
简单来理解DBSCAN便是：找出一个核心对象所有密度可达的样本集合形成簇。首先从数据集中任选一个核心对象A，找出所有A密度可达的样本集合，将这些样本形成一个密度相连的类簇，直到所有的核心对象都遍历完。DBSCAN算法的流程如下图所示：

在第1-7行中,算法先根据给定的邻域参数找出所有核心对象；
然后在第10-24行中,以任一核心对象为出发点,找出由其密度可达的样本生成聚类簇,直到所有核心对象均被访问过为止.

4. 层次聚类

层次聚类是一种基于树形结构的聚类方法，常用的是自底向上的结合策略（AGNES算法）。假设有N个待聚类的样本，其基本步骤是：

1. 初始化–>把每个样本归为一类，计算每两个类之间的距离，也就是样本与样本之间的相似度；
2. 寻找各个类之间最近的两个类，把他们归为一类（这样类的总数就少了一个）；
3. 重新计算新生成的这个类与各个旧类之间的相似度；
4. 重复2和3直到所有样本点都归为一类，结束。

可以看出其中最关键的一步就是计算两个类簇的相似度，这里有多种度量方法：

• 单链接（single-linkage）:取类间最小距离。
  
• 全链接（complete-linkage）:取类间最大距离
  
• 均链接（average-linkage）:取类间两两的平均距离
  

显然,最小距离由两个簇的最近样本决定,最大距离由两个簇的最远样本决定,而平均距离则由两个簇的所有样本共同决定。

层次聚类法的算法流程如下所示：

5. 后记

5.1 KNN与K-means区别？

K最近邻(k-Nearest Neighbor，KNN)分类算法，是一个理论上比较成熟的方法，也是最简单的机器学习算法之一。

KNN	K-Means
1.KNN是分类算法 2.属于监督学习 3.训练数据集是带label的数据	1.K-Means是聚类算法 2.属于非监督学习 3.训练数据集是无label的数据，是杂乱无章的，经过聚类后变得有序，先无序，后有序。
没有明显的前期训练过程，属于memory based learning	有明显的前期训练过程
K的含义：一个样本x，对它进行分类，就从训练数据集中，在x附近找离它最近的K个数据点，这K个数据点，类别c占的个数最多，就把x的label设为c。	K的含义：K是人工固定好的数字，假设数据集合可以分为K个蔟，那么就利用训练数据来训练出这K个分类。

相似点

都包含这样的过程，给定一个点，在数据集中找离它最近的点。即二者都用到了NN(Nears Neighbor)算法思想。

5.2 聚类算法如何评估

由于数据以及需求的多样性，没有一种算法能够适用于所有的数据类型、数 据簇或应用场景，似乎每种情况都可能需要一种不同的评估方法或度量标准。例 如，K均值聚类可以用误差平方和来评估，但是基于密度的数据簇可能不是球形， 误差平方和则会失效。在许多情况下，判断聚类算法结果的好坏强烈依赖于主观 解释。尽管如此，聚类算法的评估还是必需的，它是聚类分析中十分重要的部分之一。

聚类评估的任务是估计在数据集上进行聚类的可行性，以及聚类方法产生结 果的质量。这一过程又分为三个子任务。

1. 估计聚类趋势。

   这一步骤是检测数据分布中是否存在非随机的簇结构。如果数据是基本随机的，那么聚类的结果也是毫无意义的。我们可以观察聚类误差是否随聚类类别数量的增加而单调变化，如果数据是基本随机的，即不存在非随机簇结构，那么聚类误差随聚类类别数量增加而变化的幅度应该较不显著，并且也找不到一个合适的K对应数据的真实簇数。

2. 判定数据簇数。

   确定聚类趋势之后，我们需要找到与真实数据分布最为吻合的簇数，据此判定聚类结果的质量。数据簇数的判定方法有很多，例如手肘法和Gap Statistic方 法。需要说明的是，用于评估的最佳数据簇数可能与程序输出的簇数是不同的。 例如，有些聚类算法可以自动地确定数据的簇数，但可能与我们通过其他方法确定的最优数据簇数有所差别。

3. 测定聚类质量。

   在无监督的情况下，我们可以通过考察簇的分离情况和簇的紧 凑情况来评估聚类的效果。定义评估指标可以展现面试者实际解决和分析问题的 能力。事实上测量指标可以有很多种，以下列出了几种常用的度量指标，更多的 指标可以阅读相关文献。

   轮廓系数、均方根标准偏差、R方（R-Square）、改进的HubertΓ统计。