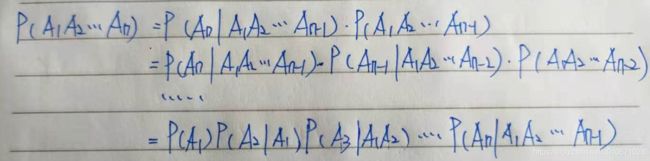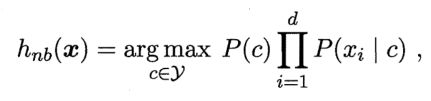机器学习--贝叶斯模型（6）

一、概念及公式

1.1 条件概率公式

①、 设A、B是两个事件，且P(A)>0，

称 P(B｜A)=P(AB)/P(A) 为在事件A发生的条件下事件B发生的条件概率。

其中P(A|B) = P(B|A)P(A) / P(B) 为贝叶斯公式

如果事件B1、B2、B3…Bn 构成一个完备事件组，即它们两两互不相容，其和为全集;并且P(Bi)大于0，则对任一事件A有

P(A)=P(A|B1)*P(B1) + P(A|B2)*P(B2) + … + P(A|Bn)*P(Bn).为全概率公式

1.2 变形得到乘法公式：

P(AB)＝P(A) P(B｜A)
P(AB)＝P(A) P(B｜A)

乘法公式推广：

一般地，设A1，A2，…，An为n≥2个事件，且P(A1A2…An-1)＞0，则有

P(A1A2…An)=P(A1)P(A2｜A1)P(A3｜A1A2)…P(An｜A1A2…An-1)

推导过程：

1.3 先验概率和后验概率

先验概率： 通过经验来判断事情发生的概率，就是先验概率。
后验概率： 就是发生结果之后，推测原因的概率。

二、贝叶斯分类器

2.1 贝叶斯决策论

在所有概率已知的理想情况下，贝叶斯决策论考虑的是如何基于这些概率和误判损失来选择最优的类别

①、基本原理：

对于N分类问题，即Y∈（c₁，c₂,…,c_n），λ_ij 表示将类别为c_j的样本误判成c_i样本的损失。那么基于后验概率P(c_i|x)可以得到将样本x分成c_i类别的 期望损失，即在样本x上的条件风险。

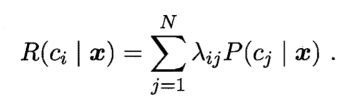
总体风险，即在各个样本上的风险的叠加。

贝叶斯判定准则：为最小化总体风险，只需在每个样本上选择那个能使条件风险最小的类别。

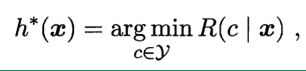
h^*(x)为贝叶斯最佳分类器，与之对应的总体风险R(h)称为贝叶斯风险。

2.2 朴素贝叶斯分类器

原理：对于给出的待分类项，求解在此项出现的条件下各个类别出现的概率，哪个最大，就认为此待分类项属于哪个类别。

利用贝叶斯公式求解后验概率P(C|X)很难操作，因为类条件概率P(X|C)是所有属性上的联合概率，难以从有限的数据集估计而得。故而朴素贝叶斯采用了“属性条件独立性假设”，即每个属性相互独立。

基于此，朴素贝叶斯分类器表达式为：

训练集可能发生某个属性值与某个类别中没有同时出现过，那么基于朴素贝叶斯分类器进行概率估计可能会出现概率值为0的情况，这样会将其他属性携带的信息失效。
因此我们常常使用“拉普拉斯修正”来进行“平滑处理”。拉普拉斯修正可以解决因样本容量不够而产生的概率估值为0的情况，但加入了噪声，会影响实际的概率估值。

2.3 朴素贝叶斯参数估计

①、极大似然估计：
②、贝叶斯估计
解决最大似然估计会出现概率值为0的情况，就是引入了拉普拉斯修正系数。

2.4 半朴素贝叶斯

半朴素贝叶斯即对属性条件独立性假设放宽了限制

三、sklearn实现

3.1 高斯朴素贝叶斯

import numpy as np
import pandas as pd
from pandas import Series, DataFrame
import matplotlib.pyplot as plt
%matplotlib inline
from sklearn.naive_bayes import GaussianNB 
from sklearn.model_selection import train_test_split 
from sklearn.datasets import make_blobs 
from sklearn.preprocessing import MinMaxScaler

#  1.建⽴数据集 
class_1 = 500 
class_2 = 500 

#两个类别分别设定500个样本 
centers = [[0.0, 0.0], [2.0, 2.0]] 
#设定两个类别的中⼼ 
clusters_std = [0.5, 0.5] 

#设定两个类别的⽅差 
X, y = make_blobs(n_samples=[class_1,class_2], centers=centers, cluster_std=clusters_std, random_state=0, shuffle=False)

# 绘制数据集图像
plt.scatter(X[:,0], X[:,1], c=y)

# 划分训练集和测试集
Xtrain, Xtest, Ytrain, Ytest = train_test_split(X,y,test_size=0.3,random_state=420)

# 2.归⼀化，确保输⼊的矩阵不带有负数 
mms = MinMaxScaler().fit(Xtrain)  # min  0 max 90 来自于Xtrain是一部分数据
Xtrain_ = mms.transform(Xtrain) 

# 拿到的所有带预测数据都应该按照建模的时候的方式处理
Xtest_ = mms.transform(Xtest)   #  100-0/90-0 > 1

# 3. 建⽴⼀个高斯朴素⻉叶斯分类器吧 
mnb = GaussianNB().fit(Xtrain_, Ytrain)

print("重要属性：调⽤根据数据获取的，每个标签类的对数先验概率 log(P(Y))")
#由于概率永远是在[0,1]之间，因此对数先验概率返回的永远是负值 
print("mnb.class_log_prior_:",mnb.class_log_prior_)
# np.unique(Ytrain)(Ytrain == 1).sum()/Ytrain.shape[0] 
print("mnb.class_log_prior_.shape:", mnb.class_log_prior_.shape)

print("可以使⽤np.exp来查看真正的概率值")
print("np.exp(mnb.class_log_prior_:",np.exp(mnb.class_log_prior_))

print("重要属性：返回⼀个固定标签类别下的每个特征的对数概率log(P(Xi|y))")
print("mnb.feature_log_prob_:",mnb.feature_log_prob_)
print("mnb.feature_log_prob_.shape:",mnb.feature_log_prob_.shape)

print("重要属性：在fit时每个标签类别下包含的样本数。\
当fit接⼝中的sample_weight被设置时，该接⼝返 回的值也会受到加权的影响 ")
print("mnb.class_count_:",mnb.class_count_)
print("mnb.class_count_.shape:",mnb.class_count_.shape)

# 查看分类器的效果？ 
#⼀些传统的接⼝ 
mnb.predict(Xtest_)
mnb.predict_proba(Xtest_)
mnb.score(Xtest_,Ytest)

3.2 多项式朴素贝叶斯

3.3 伯努利朴素贝叶斯