回归预测 | MATLAB实现SSA-LSTM(麻雀算法优化长短期记忆神经网络)多输入单输出
回归预测 | MATLAB实现SSA-LSTM(麻雀算法优化长短期记忆神经网络)多输入单输出
目录
-
-
- 回归预测 | MATLAB实现SSA-LSTM(麻雀算法优化长短期记忆神经网络)多输入单输出
- 预测效果
- 基本介绍
- 程序设计
- 参考资料
-
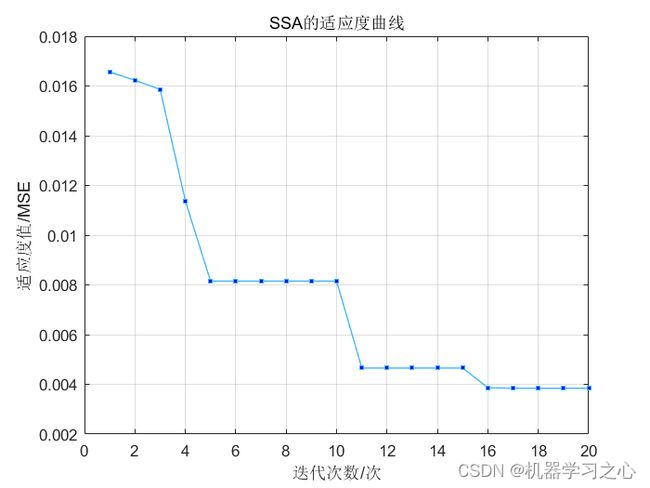
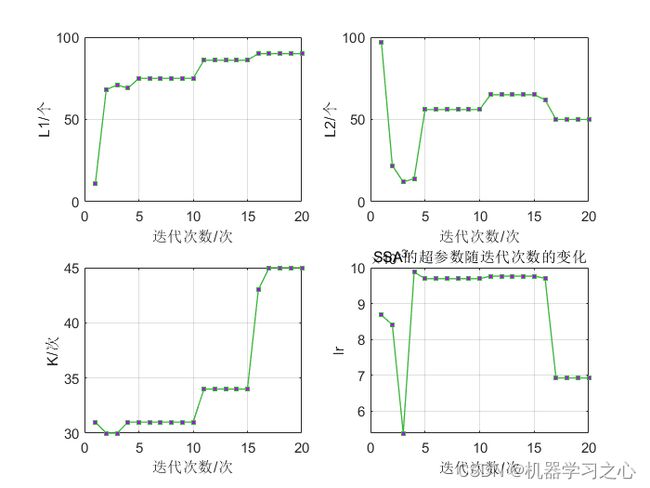
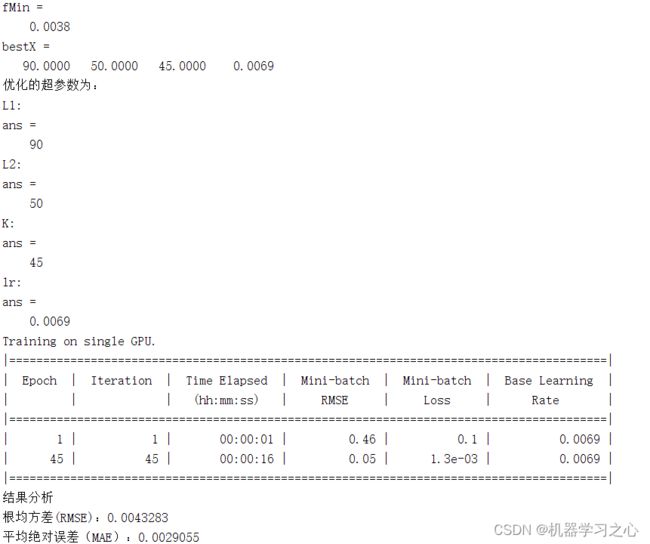
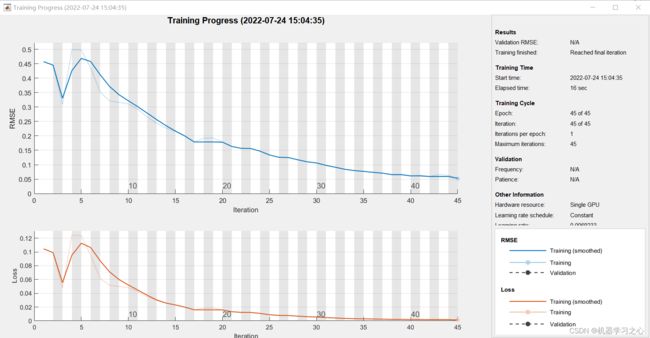
预测效果
基本介绍
麻雀搜索算法(Sparrow Search Algorithm, SSA)是于2020年提出的。SSA 主要是受麻雀的觅食行为和反捕食行为的启发而提出的。该算法比较新颖,具有寻优能力强,收敛速度快的优点。建立麻雀搜索算法的数学模型,主要规则如下所述:
(1)发现者通常拥有较高的能源储备并且在整个种群中负责搜索到具有丰富食物的区域,为所有的加入者提供觅食的区域和方向。在模型建立中能量储备的高低取决于麻雀个体所对应的适应度值(Fitness Value)的好坏。
(2)一旦麻雀发现了捕食者,个体开始发出鸣叫作为报警信号。当报警值大于安全值时,发现者会将加入者带到其它安全区域进行觅食。
(3)发现者和加入者的身份是动态变化的。只要能够寻找到更好的食物来源,每只麻雀都可以成为发现者,但是发现者和加入者所占整个种群数量的比重是不变的。也就是说,有一只麻雀变成发现者必然有另一只麻雀变成加入者。
(4)加入者的能量越低,它们在整个种群中所处的觅食位置就越差。一些饥肠辘辘的加入者更有可能飞往其它地方觅食,以获得更多的能量。
(5)在觅食过程中,加入者总是能够搜索到提供最好食物的发现者,然后从最好的食物中获取食物或者在该发现者周围觅食。与此同时,一些加入者为了增加自己的捕食率可能会不断地监控发现者进而去争夺食物资源。
(6)当意识到危险时,群体边缘的麻雀会迅速向安全区域移动,以获得更好的位置,位于种群中间的麻雀则会随机走动,以靠近其它麻雀。
长短期记忆网络——通常被称为 LSTM,是一种特殊的 RNN,能够学习长期依赖性。由 Hochreiter 和 Schmidhuber(1997)提出的,并且在接下来的工作中被许多人改进和推广。LSTM 在各种各样的问题上表现非常出色,现在被广泛使用。LSTM 被明确设计用来避免长期依赖性问题。长时间记住信息实际上是 LSTM 的默认行为,而不是需要努力学习的东西!
所有递归神经网络都具有神经网络的链式重复模块。在标准的 RNN 中,这个重复模块具有非常简单的结构
程序设计
- 完整源码私信博主
%% 参数设置
pop=5; % 种群数
M=20; % 最大迭代次数
dim=4;%一共有4个参数需要优化
lb=[1 1 1 0.001];%分别对两个lstm隐含层节点 训练次数与学习率寻优
ub=[100 100 50 0.01];%这个分别代表4个参数的上下界,比如第一个参数的范围就是1-100
P_percent = 0.2; %producers 在全部种群的占比
pNum = round( pop * P_percent ); % producers的数量
for t = 1 : M
[ ~, sortIndex ] = sort( pFit );% Sort.从小到大
[fmax,B]=max( pFit );
worse= x(B,:);
r2=rand(1);
%%%%%%%%%%%%%5%%%%%%这一部位为发现者(探索者)的位置更新%%%%%%%%%%%%%%%%%%%%%%%%%
if(r2<0.8)%预警值较小,说明没有捕食者出现
for i = 1 : pNum %r2小于0.8的发现者的改变(1-20) % Equation (3)
r1=rand(1);
x( sortIndex( i ), : ) = pX( sortIndex( i ), : )*exp(-(i)/(r1*M));%对自变量做一个随机变换
x( sortIndex( i ), : ) = Bounds( x( sortIndex( i ), : ), lb, ub );%对超过边界的变量进行去除
fit( sortIndex( i ) )=fitness(x(sortIndex( i ),:),P_train,T_train,P_test,T_test);
end
else %预警值较大,说明有捕食者出现威胁到了种群的安全,需要去其它地方觅食
for i = 1 : pNum %r2大于0.8的发现者的改变
x( sortIndex( i ), : ) = pX( sortIndex( i ), : )+randn(1)*ones(1,dim);
x( sortIndex( i ), : ) = Bounds( x( sortIndex( i ), : ), lb, ub );
fit( sortIndex( i ) )=fitness(x(sortIndex( i ),:),P_train,T_train,P_test,T_test);
end
end
[ ~, bestII ] = min( fit );
bestXX = x( bestII, : );
%%%%%%%%%%%%%5%%%%%%这一部位为加入者(追随者)的位置更新%%%%%%%%%%%%%%%%%%%%%%%%%
for i = ( pNum + 1 ) : pop %剩下的个体的变换 % Equation (4)
% i
% sortIndex( i )
A=floor(rand(1,dim)*2)*2-1;
if( i>(pop/2))%这个代表这部分麻雀处于十分饥饿的状态(因为它们的能量很低,也是是适应度值很差),需要到其它地方觅食
x( sortIndex(i ), : )=randn(1,dim).*exp((worse-pX( sortIndex( i ), : ))/(i)^2);
else%这一部分追随者是围绕最好的发现者周围进行觅食,其间也有可能发生食物的争夺,使其自己变成生产者
x( sortIndex( i ), : )=bestXX+(abs(( pX( sortIndex( i ), : )-bestXX)))*(A'*(A*A')^(-1))*ones(1,dim);
end
x( sortIndex( i ), : ) = Bounds( x( sortIndex( i ), : ), lb, ub );%判断边界是否超出
fit( sortIndex( i ) )=fitness(x(sortIndex( i ),:),P_train,T_train,P_test,T_test);
end
%%%%%%%%%%%%%5%%%%%%这一部位为意识到危险(注意这里只是意识到了危险,不代表出现了真正的捕食者)的麻雀的位置更新%%%%%%%%%%%%%%%%%%%%%%%%%
c=randperm(numel(sortIndex));%%%%%%%%%这个的作用是在种群中随机产生其位置(也就是这部分的麻雀位置一开始是随机的,意识到危险了要进行位置移动,
%处于种群外围的麻雀向安全区域靠拢,处在种群中心的麻雀则随机行走以靠近别的麻雀)
b=sortIndex(c(1:3));
for j = 1 : length(b) % Equation (5)
if( pFit( sortIndex( b(j) ) )>(fMin) ) %处于种群外围的麻雀的位置改变
x( sortIndex( b(j) ), : )=bestX+(randn(1,dim)).*(abs(( pX( sortIndex( b(j) ), : ) -bestX)));
else
%处于种群中心的麻雀的位置改变
x( sortIndex( b(j) ), : ) =pX( sortIndex( b(j) ), : )+(2*rand(1)-1)*(abs(pX( sortIndex( b(j) ), : )-worse))/ ( pFit( sortIndex( b(j) ) )-fmax+1e-50);
end
x( sortIndex(b(j) ), : ) = Bounds( x( sortIndex(b(j) ), : ), lb, ub );
fit( sortIndex( b(j) ) )=fitness(x(sortIndex( b(j) ),:),P_train,T_train,P_test,T_test);
end
参考资料
[1] https://blog.csdn.net/article/details/126072792?spm=1001.2014.3001.5502
[2] https://blog.csdn.net/article/details/126044265?spm=1001.2014.3001.5502
[3] https://blog.csdn.net/article/details/126043107?spm=1001.2014.3001.5502