【图像处理笔记3】Gabor Filter的手动和调包实现
Gabor filter 作为一种很出名的纹理滤波器，可以很好的捕捉纹理信息。一个2d的gabor filter的实数部分如下：
G ( x , y ; λ , σ , γ , θ , ψ ) = e x p ( − x ′ 2 + γ 2 y ′ 2 2 σ 2 ) c o s ( 2 π x ′ λ + ψ ) G(x, y; \lambda, \sigma, \gamma, \theta, \psi) = exp(-\frac{x'^2+\gamma^2 y'^2}{2\sigma^2})cos(2\pi\frac{x'}{\lambda} + \psi) G(x,y;λ,σ,γ,θ,ψ)=exp(−2σ2x′2+γ2y′2)cos(2πλx′+ψ)
把cos改成sin就是虚数部分，如果要写成完全形式就是：
G ( x , y ; λ , σ , γ , θ , ψ ) = e x p ( − x ′ 2 + γ 2 y ′ 2 2 σ 2 ) e x p ( i ( 2 π x ′ λ + ψ ) ) G(x, y; \lambda, \sigma, \gamma, \theta, \psi) = exp(-\frac{x'^2+\gamma^2 y'^2}{2\sigma^2})exp(i(2\pi\frac{x'}{\lambda} + \psi)) G(x,y;λ,σ,γ,θ,ψ)=exp(−2σ2x′2+γ2y′2)exp(i(2πλx′+ψ))
在图像处理时，只用实数部分，并且可以变形成：
G ( x , y ; λ , σ x , σ y , θ ) = e x p ( − x ′ 2 σ x 2 − y ′ 2 σ y 2 ) c o s ( 2 π x ′ λ ) G(x, y; \lambda, \sigma_x, \sigma_y, \theta) = exp(-\frac{x'^2}{\sigma_x^2} - \frac{y'^2}{\sigma_y^2})cos(2\pi\frac{x'}{\lambda}) G(x,y;λ,σx,σy,θ)=exp(−σx2x′2−σy2y′2)cos(2πλx′)
其中 x ′ = x c o s θ + y s i n θ , y ′ = − x s i n θ + y c o s θ x' = x cos\theta + y sin\theta, y' = -x sin\theta + y cos\theta x′=xcosθ+ysinθ,y′=−xsinθ+ycosθ. θ \theta θ 是方向， λ \lambda λ 是波长。现在的Gabor由4个参数控制（ λ , σ x , σ y , θ \lambda, \sigma_x, \sigma_y, \theta λ,σx,σy,θ）.
代码实现如下, 代码里的freq就是 λ \lambda λ：
import math
def gaborFn(sigma_x, sigma_y, theta, freq):
sz_x = 6*sigma_x+1
sz_y = 6*sigma_y+1
sz_xx = np.arange(-np.fix(sz_x/2),np.fix(sz_x/2)+1)
sz_yy = np.arange(np.fix(-sz_y/2),np.fix(sz_y/2)+1)
x, y = np.meshgrid(sz_xx, sz_yy)
x_theta=x*np.cos(theta)+y*np.sin(theta)
y_theta=-x*np.sin(theta)+y*np.cos(theta)
# gabor[y, x] = np.exp(-(_x**2 + Gamma**2 * _y**2) / (2 * Sigma**2)) * np.cos(2*np.pi*_x/Lambda + Psi)
gb=np.exp(-0.5*(x_theta**2/sigma_x**2+y_theta**2/sigma_y**2))*np.cos(2*math.pi*freq*x_theta)
return x, y, gb
比如设置成（3， 3， math.pi/2， 0.5）的参数
x, y, gb = gaborFn(3, 3, math.pi/2, 0.5)
plt.imshow(gb, cmap = plt.cm.gray)
3D图画出来是这样
x = np.linspace(-10, 10, 13)
y = np.linspace(-10, 10, 13)
x, y = np.meshgrid(x,y)
_, _, gb = gaborFn(2, 2, math.pi/2, 0.5)
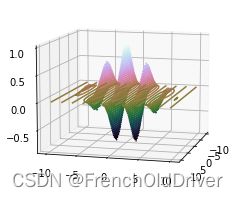
fig = plt.figure()
ax = plt.axes(projection='3d')
ax.contour3D(x,y,gb,50,cmap='cubehelix')
ax.view_init(10, 15)
plt.show()
Gabor还可以用过skimage 调包实现
from skimage.filters import gabor_kernel
gabors = gabor_kernel(frequency = 0.5, theta = 0, sigma_x = 2, sigma_y = 2)
plt.imshow(np.real(gabors),plt.cm.gray )
显示的时候要用np.real取实数部分，不然画不出来