浅谈基于数据结构Graph的路径规划

一.理论浅述

在学习算法的时候，我们经常遇到了一类路径规划问题，对题目简单归纳，他们大致分为两类：

1. 最短路径的规划安排
2. 最快路径的规划安排

这里就分享一下我在学习过程中的一些的认识

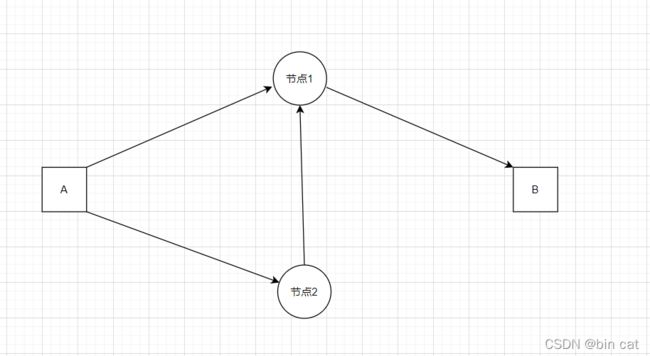
如图所示：

若要从A到B，显而易见如果我们假设每一段都是一样长，所花时间都一样，我们的选择肯定会是：A-->节点1-->B，这就是所谓的最短路径

对于这种情况，我们的解决办法可以是创造一个顺序查找序列，即一层一层往外查，首先查A起始节点，连有节点1和节点2，判断节点1和节点2是否为终止节点，若有则停止，若无则向外查找，直到查找到终止节点，输出最终查找的次数即为最短路径，类似于队列思想，总是先将需要转移次数更少的状态进行分析处理

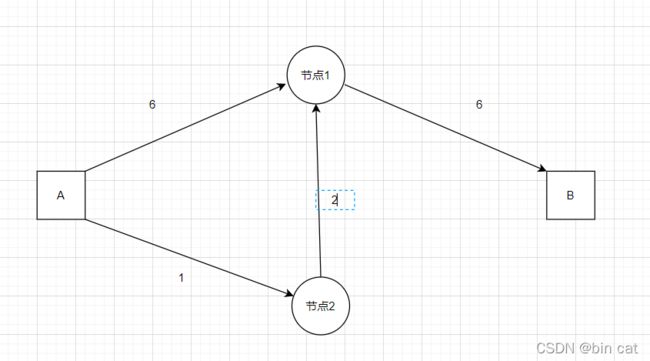
而另外一种则是这样的

可以发现路径被加上了通过时间，也就是按照这个题目的 设定，我们要找到从A到B的最快路径即为：A-->节点2-->节点1-->B 这就是所谓的最短时间

对于这种情况，我们可以使用狄克斯特拉算法，计算加权图中的最短路径，相较于上面的一种情况，在这种情况下我们不但要记录下一位检索的节点是谁，还要记录到下一个节点所要付出的“代价”（权数），这里我们会用到三个表，第一记录相邻节点，第二记录相邻节点的代价，第三记录父子节点的关系，最后记录已经遍历过的节点，重复如此直到B点出现。但是该算法也有许多缺点，受到的限制很大，要求是无环有向图且权数不能为负数，

方法大概就是这样

二.例题

下面是两个简单的例题

类型一（BFS算法）

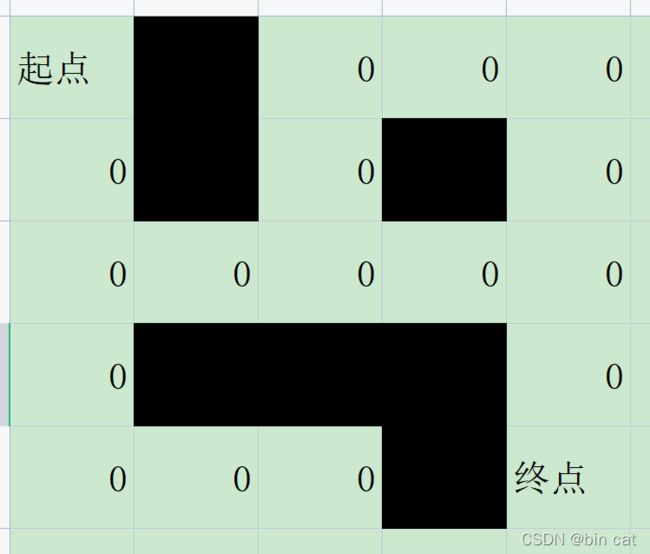
假定有一个迷宫maze，其中的1表示墙壁，0表示可以走的路，只能横着走或竖着走，不能斜着走，求从左上角到右下角的最短路线。

 maze[5][5]
0, 1, 0, 0, 0,
0, 1, 0, 1, 0,
0, 0, 0, 0, 0,
0, 1, 1, 1, 0,
0, 0, 0, 1, 0,

 按照上面提到的处理方法可以将元素的邻居进行编号区分度数

 

 由此将有效格子编号之后就可以画出BFS树（这个比较简单就不画了）

下面代码分析一下

首先定义一个类接收x,y值 ，

class Node:
    def __init__(self, x, y):
        self.x = x
        self.y = y

创建接收的main函数

def main():
    n, m = map(int, input("请输入迷宫的长宽（用逗号分割）：").split(','))
    maze = []
    for i in range(n):
        maze.append([])
    for i in range(n):
        for j in range(m):
            maze[i].append('')
    begin = Node(0,0)
    end = Node(m-1,n-1)
    for i in range(n):   #接收地图
        s = input()
        maze[i] = list(s)
    BFS_search(n,m,maze, begin, end)

下面就是按照上面的理论造出来一个BFS_search函数了，因为要运用队列，所以这边引入collections

def BFS_search(n,m,maze, begin, end):
    strange = [[maxx for i in range(m)] for j in range(n)]  #设定未探索区域，大小和迷宫相当
    dx = [1, 0]  
    dy = [0, 1]
    sx, sy = begin.x, begin.y
    gx, gy = end.x, end.y
    strange[sx][sy] = 0
    search_queue = deque()
    search_queue.append(begin)
    while search_queue:
        current = search_queue.popleft()
        find = False
        for i in range(2):  #只存在向下或向右运动
            nx, ny = current.x + dx[i], current.y + dy[i]
            if maze[nx][ny] != '#' and strange[nx][ny] == maxx and 0 <= nx < n and 0 <= ny < m :  #判断是否在地图内是否撞墙
                strange[nx][ny] = strange[current.x][current.y] + 1
                search_queue.append(Node(nx, ny))
                if nx == gx and ny == gy:  #探查到边界
                    find = True
                    break
        if find:
            break
    print(f'最短路径的长度：{strange[gx][gy]:02d}')      

大体完成，引库触发

from collections import deque

maxx = float("inf")

if __name__ == '__main__':
    main()

类型二 （考虑到可能出现的负权数这里我们就不使用狄克斯特拉算法）

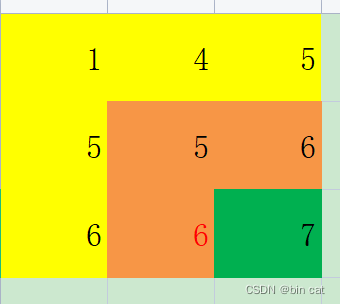
给定一个包含非负整数的 m*n的网格grid，请找出一条从左上角到右下角的路径，使得路径上的数字总和为最小。

输入：grid = [[1,3,1],[1,5,1],[4,2,1]]
输出：7

将示例作为研究对象

 首先我们应该可以想到DFS算法，通过画出DFS树，采用回溯的方法找到最短路径，但这样虽然最容易想到但是存在重复处理的情况，需要添加记忆化搜索，显然这不是这道题目的最优解，相比之下使用dp能降低编程的复杂度

对于这道题，dp算法中我们的总问题可表达为dp[i][j],表示从起始点到终点的最短路径，子问题就是点（i，j）到终点的距离

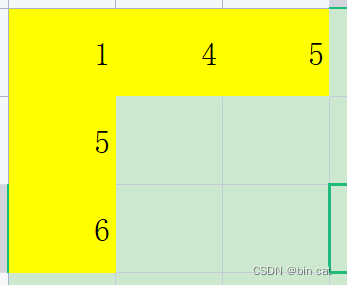
这里我先特殊化处理第一行第一列如图

for i in range(1,lie):
    graph[0][i] += graph[0][i-1]
for j in range(1,hang):
    graph[j][0] += graph[j-1][0]

后面就是处理出去第一行和第一列的数据，min（取最小值）如图，这样思路就很清晰了

for xx in range(1,hang):
            for xxx in range(1,lie):
                graph[xx][xxx] += min(graph[xx-1][xxx],graph[xx][xxx-1])

综上我们的dp（）就可以写成

def dp(graph):
    hang=len(graph)
    lie=len(graph[1])
    for i in range(1,lie):
        graph[0][i] += graph[0][i-1]
    for j in range(1,hang):
        graph[j][0] += graph[j-1][0]
    for xx in range(1,hang):
            for xxx in range(1,lie):
                graph[xx][xxx] += min(graph[xx-1][xxx],graph[xx][xxx-1])
    return graph[hang-1][lie-1]

这样就出来了

三.总结

图这个数据结构，很容易拿来出题，他涉及的算法方面很广，使用DFS和BFS只是冰山一角，而且这种题目一出来难度也是非常可观的，对于研究算法技巧和提升编程思维有很大的帮助，是日后可以好好玩玩的东西，本文可能很多地方显得荒谬，望各位师傅们谅解。

                                                                                                                                 20网安b1nc3t