随机数就是随机产生的数-_-||，分为两种：真随机数(random number)和伪随机数(pseudo-random number)。自然界由很多复杂因素产生的现象量化后的数（比如掷骰子）是真正随机的，就是真随机数。
一般意义上的电子计算机是确定系统，常规方法无法产生真随机数，而且真随机数的统计指标（原点矩、方差等）不一定好，且无法“重现”，故计算机常用伪随机数，又称为伪随机序列（pseudo-random sequence）。
/***************************加乘混合同余法****************************/
伪随机序列生成法有很多种，有取中法、移位法、同余法，近年来还有Gold序列（用于LTE系统加密）等等。
一般来说，伪随机序列常用[0,1]上的均匀分布，需要其他分布时，可以用概率积分变换快速地转换为其他分布
其中，生成算法比较简单，性能也比较高的算法是同余法中的加乘混合同余法，其公式表示为：
其中C和 λ为常数，且C不为0， λ不为1（C=0是乘法同余法，λ=1是加法同余法）。
由于要得到[0,1]上的序列，于是
以下不加证明（其实是我没找到，求高手给证明）地给出随机序列周期达到M的充要条件为：
1 )c 与M 互素;
2 ) 对每一个M 的素因子p ,λ - 1为p 的倍数;
3 ) 若M 是4 的倍数,那么λ- 1 是4 的
倍数.
由以上条件易知，在2 进制计算机上,若,应取λ =4q + 1 ,c = 2 a + 1 ,为任意非负整数,其中q,a为正整数.
它的一个致命的弱点，那就是随机数的生成在某一周期内成线性增长的趋势，显然，在大多数场合，这种极富“规律”型的随机数是不应当使用的。
/****************随机序列质量的衡量指标***************************/
1、均匀性
比如以0.5为界，左右两边应几乎各占一半
2、覆盖性
对模拟需要的值，应几乎全部取到，不应有遗漏
3、循环性
不论序列有多长，应构成一个首尾相连的闭环序列
4、非循环性
这个意思是说“循环要足够长”，之前说循环性是指“能回来”，这里指“不能还没模拟完就回来”
5、独立性
随机序列应只取决于随机生成算法
6、检验性
随机函数要能经得起各种统计检验
7、系统开销要小
这个是大多数程序要求的，时间复杂度和空间复杂度要尽量低。
/*************蒙特卡罗方法*************************************/
Monte Carlo 方法的要点是:对要解决的数值计算问题,构造适当的概率模型,使要得到的解正好
重合于概率模型中随机变量的概率分布或数字特征,其后在计算机上用伪随
机数列对随机变量进行模拟得到一个大子样的观测数据,进行统计整理以后,给出问题的一个近似估计. 因此,Monte Carlo方法是双重近似,一是将数值计算问题用概率模型作近似,二是在计算机上用伪随机数作近似抽样值进行统计整理作出一些估计.
设g ( x ) 是[0 ,1 ] 上的连续函数, 且0 ≤ g ( x )≤1 . 考虑定定积分
的值，那么由y=g(x)、y=0、x=0、x=1围成的图形面积就是S，如果在单位正方形(0,0,1,1)内均匀地投点(x , y ) ,则该随机点落入曲线y = g ( x ) 下阴影的概率：
向正方形0 ≤x ≤1 ,0 ≤y ≤1 内均匀投点 ,ξi ,ηi 是相互独立的均匀随机数列,第i 次试验成
功,即 落入A 中,也就是满足ηi ≤g (ξi ) ,若每次成功的概率为p ,进行n 次试验成功了k 次,则由大数定理知
即n 充分大时, k/ n 依概率收敛到p . 由于p = s ,因此常取s ≈ k/ n .
于是，一个伪随机序列的质量可以用蒙特卡罗方法验证
/*****************翠花，上代码*********************************/
我们取
$M=2^30=1073741824$
$\lambda=129$
C=129
写的比较难看，大家凑合看一下吧……
C++代码
2 #define M 1073741824
3 #define K 129
4 #define C 17
5 #define N 100000
6 const int n = 3 ;
7 using namespace std;
8 long long t;
9
10 /* *********加乘混合同余法************* */
11 double rand(){
12 double x;
13 t = (K * t + C) % M; // t=Kt+c (mod M)
14 x = double (t) / M;
15 return x;
16 }
17
18 /* ************乘方计算*************** */
19 long double power( long double x, long double n){
20 long double y = x;
21 for ( int i = 1 ;i < n;i ++ )
22 y *= x;
23 return y;
24 }
25
26 /* ********** 蒙特卡罗积分法 ******** */
27 long double integrate( long double x[], long double y[]){
28 long double s;
29 long k = 0 ;
30 for ( int i = 0 ;i < N;i ++ ){
31 if (y[i] <= power(x[i],n))
32 k ++ ;
33 }
34 s = ( long double )k / N;
35 return s;
36 }
37
38 int main(){
39 long double x[N],y[N],s = 0.0 ,s2 = 0.0 ,d,e;
40 int i;
41 t = 124 ;
42 for (i = 0 ;i < N;i ++ ){
43 x[i] = rand();
44 s = s + x[i]; // 累加
45 cout << x[i] << endl;
46 }
47 t = 54 ;
48 for (i = 0 ;i < N;i ++ ){
49 y[i] = rand();
50 }
51 e = s / N; // 平均数
52 for (i = 0 ;i < N;i ++ ){
53 s2 += (x[i] - e) * (x[i] - e);
54 d = s2 / (N - 1 ); // 方差 dafdq
55 }
56 cout << " The average is " << e
57 << " ,which is 0.5 theoretically " << endl << endl;
58 cout << " The mean square deviation is " << d
59 << " ,which is 0.08333333 theoretically " << endl << endl;
60 cout << " Intgreate resault is " << integrate(x,y)
61 << " ,which is " << ( double ) 1 / (n + 1 ) << " theoretically " << endl << endl;
62 return 0 ;
63 }
给结果（序列太长了，略去）
The average is 0.500178,which is 0.5 theoretically
The mean square deviation is 0.0833717,which is 0.08333333 theoretically
Integreate result is 0.24989,which is 0.25 theoretically
%%%%%%%%%%%%Matlab程序%%%%%%%%%%%%%%%%%%%%%
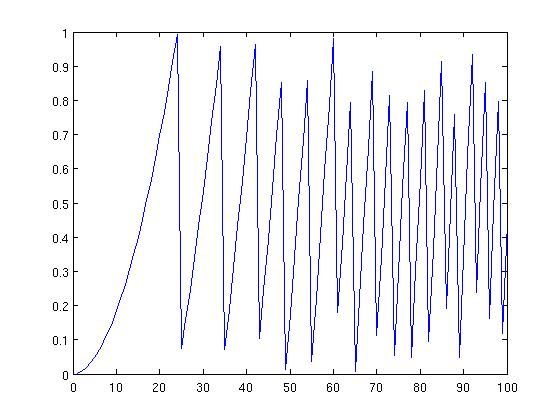
用matlab测试的时候发现，先前选取的λ=65537并不好，在N=1000时，产生的序列是这样的
一块一块的很难看，
把N降到一百
非常明显的线性，这个缺点很大了！
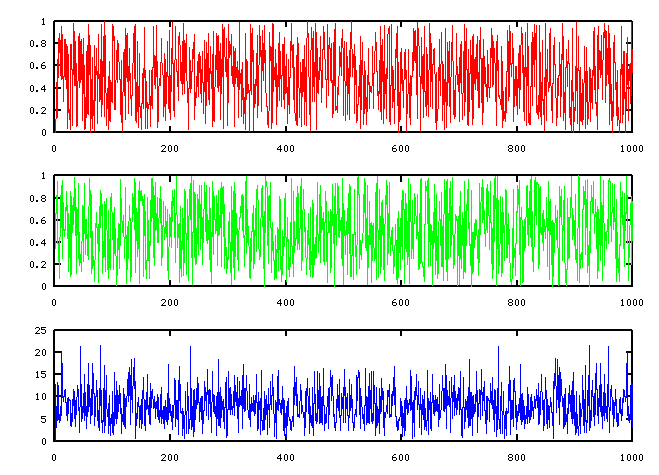
所以我换了参数，并且与matlab自带的rand()进行了比较
M = 2 ^ 32 ;
k = 129 ;
C = 53 ;
x( 1 ) = 63343 ;
r( 1 ) = 63343 / M;
n = 1000 ;
m = rand(n, 1 );
for i = 2 :n
x(i) = mod (k * x(i - 1 ) + C,M);
r(i) = x(i) / M;
end
i = 1 :n;
subplot( 311 )
plot(i,r, ' -r')
subplot( 312 )
plot(i,m, ' -g');
b = fft(r);
c = abs (b);
c( 1 ) = 0 ; %0点有bug
subplot( 313 )
plot(c);
其中绿色的是matlab自带函数生成的序列，蓝色的是频谱图
*参考文献
[1] 郭继展 过勇 苏辉 . 程序算法与技巧精选 ，机械工业出版社，2008
[2]郑 列, 宋正义 伪随机数生成算法及比较 ，湖北工业大学学报，2008 年10 月