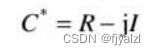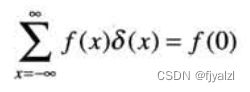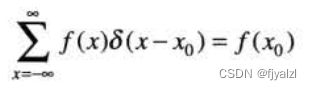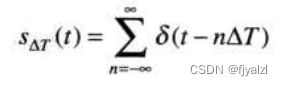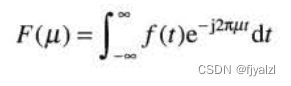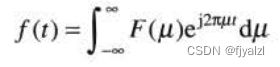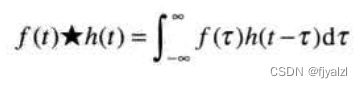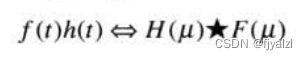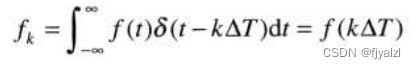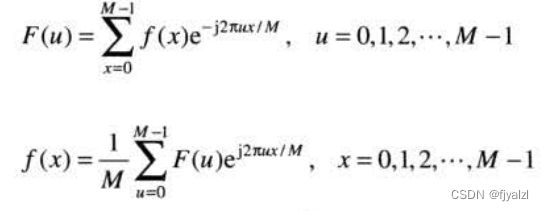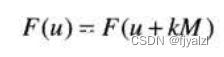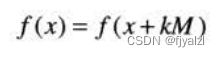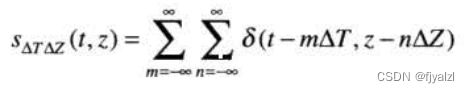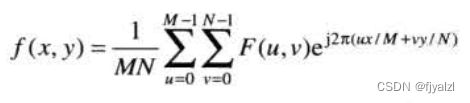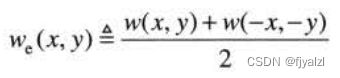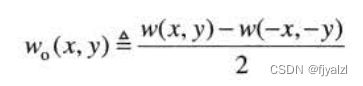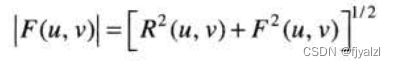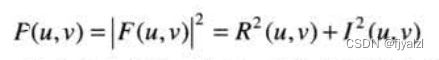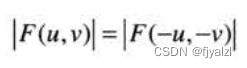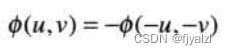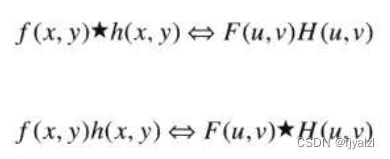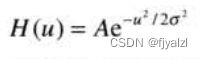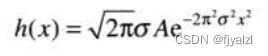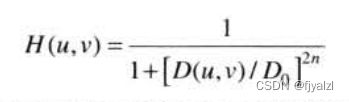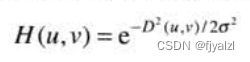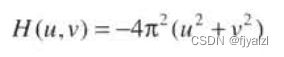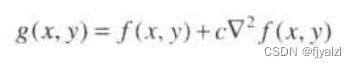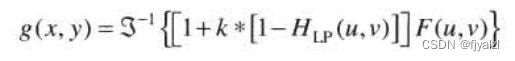数字图像处理第四章——频率域滤波
目录
4.1 基本概念
4.1.1 复数
4.1.2 傅立叶级数
4.1.3 冲激及其取样特性
4.1.4 连续变量函数的傅里叶变换
4.1.5 卷积
4.2 取样和取样函数的傅里叶变换
4.2.1 取样
4.2.2 取样函数的傅里叶变换
4.3 单变量的离散傅里叶变换(DFT)
4.3.1 由取样后的函数的连续变换得到DFT
4.4 两个变量的函数的拓展
4.4.1 二维冲激及其取样
4.4.2 二维连续傅里叶变化对
4.4.3 二维取样和二维取样定理
4.4.4 二维离散傅里叶变换及其反变换
4.5 二维离散傅里叶变换的一些性质
4.5.1 空间和频率间隔的关系
4.5.2 平移和旋转
4.5.3 周期性
4.5.4 对称性
4.5.5 傅里叶谱和相角
4.5.6 二维卷积定理
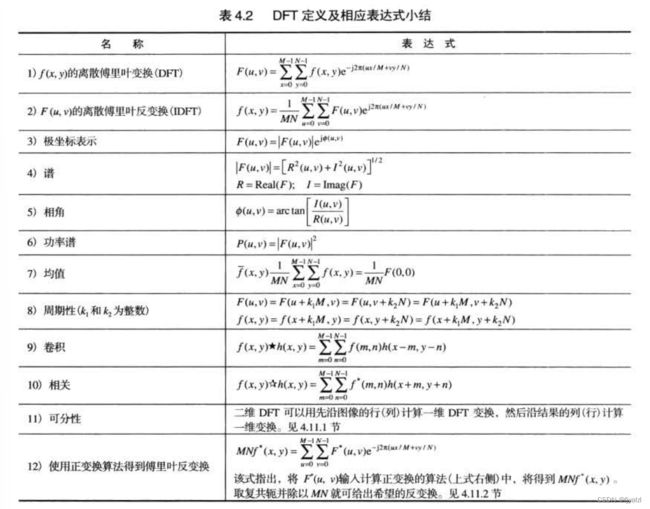
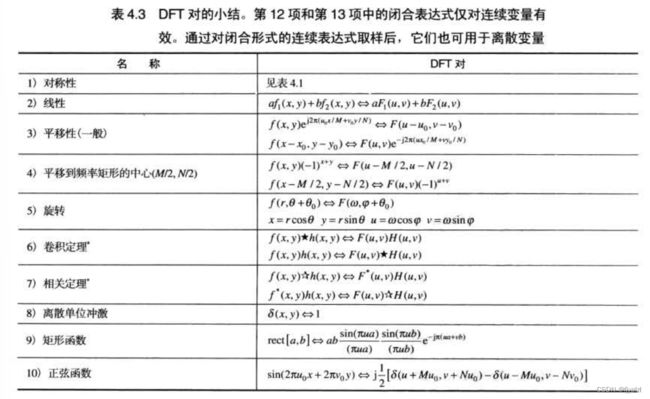
4.5.7 二维离散傅里叶变换性质的小结
4.6 频率域滤波基础
4.6.1 频率域滤波基础
4.6.2 频率域滤波步骤小结
4.6.3 空间和频率域滤波间的对应
4.7 使用频率表与滤波器平滑图像
4.7.1 理想低通滤波器
4.7.2 布特沃斯低通滤波器
4.7.3 高斯低通滤波器
4.8 使用频率域滤波器锐化图像
4.8.1 理想高通滤波器
4.8.2 布特沃斯高通滤波器
4.8.3 高斯高通滤波器
4.8.4 频率域的拉普拉斯算子
4.8.5 钝化模板、高提升滤波和高频强调滤波
4.9 选择性滤波
4.9.1 带阻滤波器和带通滤波器
4.9.2 陷波滤波器
4.1 基本概念
4.1.1 复数
复数C定义如下:
式中,R和I是实数,j是一个等于-1的平方根的虚数,即 。R表示复数的实部,I表示复数的虚部。
。R表示复数的实部,I表示复数的虚部。
实数是I=0的复数的子集。复数C的共轭表示为C*,其定义是
欧拉公式:
欧拉公式极坐标下的复数表示:
![]()
4.1.2 傅立叶级数
具有周期T的连续变量t的周期函数f(t)可描述为乘以适当系数的正弦和余弦之和。这个和就是傅立叶级数
式中,
是系数。
4.1.3 冲激及其取样特性
一个冲激具有关于如下积分的所谓取样特性:
假设 f(t)在t=0处是连续的,取样特性得到函数f(t)在冲激位置的值。取样特性的一种更为一般的说明涉及位于任意点t0的冲激,表示为![]() 。这种情况下取样特性变为:
。这种情况下取样特性变为:
离散变量的取样特性有如下形式:
更一般地用位置x=x0处的离散冲激
冲激串定义为无限多个离散的周期冲激单元△T之和:
4.1.4 连续变量函数的傅里叶变换
连续变量t的连续函数f(t)的傅里叶变换由下式定义:
也可写成
利用欧拉公式,可把第二个式子表示为:
![]()
4.1.5 卷积
卷积的定义如下
卷积定理:
4.2 取样和取样函数的傅里叶变换
4.2.1 取样
取样后函数表示为:
该式每个成分都是由该冲激位置处f(t)的值加权后的冲激。每个取样值由加权后的冲激“强度”给出,我们可通过积分得到它。也就是说,序列中的任意取样值fk由下式给出:
4.2.2 取样函数的傅里叶变换
其中,
可得到F(μ)和S(μ)的卷积:
4.3 单变量的离散傅里叶变换(DFT)
4.3.1 由取样后的函数的连续变换得到DFT
傅里叶正变换和反变换都是无限周期的,其周期为M,即:
和
4.4 两个变量的函数的拓展
4.4.1 二维冲激及其取样
两个连续变量t和z的冲激定义为如下形式:
对于二维离散变量,其冲激定义为
取样特性为
对于坐标(x0,y0)外的冲激,取样特性为
4.4.2 二维连续傅里叶变化对
令f(t,z)是两个连续变量t和z的连续函数。则其二维连续傅里叶变换对由以下两个表达式给出:
式中,μ和v是频率变量。当涉及图像时,t和z解释为连续空间变量。就像一维情况那样,变量μ和v的域定义了连续频率域。
4.4.3 二维取样和二维取样定理
二维取样可用取样函数(二维冲激串)建模:
4.4.4 二维离散傅里叶变换及其反变换
二维傅里叶变换(DFT)为:
反变换(IDFT)为:
4.5 二维离散傅里叶变换的一些性质
4.5.1 空间和频率间隔的关系
假定对连续函数f(t,z)取样生成了一幅数字图像f(x,y),它由分别在t和z方向所取的MxN个样点组成。令△T和△Z表示样本间的间隔。那么,相应离散频率域变量间的间隔分别由
给出。频率域样本间的间隔与空间样本间的间距及样本数成反比。
4.5.2 平移和旋转
平移特性:
4.5.3 周期性
二维傅里叶变换及其反变换在u方向和v方向是无限周期的
4.5.4 对称性
任意实函数或复函数w(x,y)均可表示为一个奇数部分和一个偶数部分(其中每个都可以是实部或虚部)的和:
其中,偶数部分和奇数部分定义如下:
偶函数是对称的,奇函数是反对称的。
4.5.5 傅里叶谱和相角
使用极坐标形式表示二维DFT:
其中幅度
称为傅里叶谱(或频谱),而
称为相角。
功率谱定义为
R和I分别是F(u,v)的实部和虚部,并且,所有的计算直接对离散变量u=0,1,2,...,M-1和v=0,1,2,...,N-1进行。![]()
实函数的傅里叶变换是共轭对称的,这表明谱是关于原点偶对称的:
相角关于原点奇对称:
它指出零频率项与f(x,y)的平均值成正比,从而有
4.5.6 二维卷积定理
二维循环卷积表达式:
二维卷积定理由下面的表达式给出:
4.5.7 二维离散傅里叶变换性质的小结
代码实现:
import os
import numpy as np
import cv2
import matplotlib.pyplot as plt
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False
def put(path):
img = cv2.imread(path, 1)
# img = cv2.imread(os.path.join(base, path), 1)
img = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY)
rows, cols = img.shape[:2]
# 傅里叶变换
dft = cv2.dft(np.float32(img), flags=cv2.DFT_COMPLEX_OUTPUT)
# 将频谱低频从左上角移动至中心位置
dft_shift = np.fft.fftshift(dft)
# 频谱图像双通道复数转换为0-255区间
res1 = 20 * np.log(cv2.magnitude(dft_shift[:, :, 0], dft_shift[:, :, 1]))
# 傅里叶逆变换
ishift = np.fft.ifftshift(dft_shift)
iimg = cv2.idft(ishift)
res2 = cv2.magnitude(iimg[:, :, 0], iimg[:, :, 1])
# 图像顺时针旋转60度
M = cv2.getRotationMatrix2D((cols / 2, rows / 2), -60, 1)
rot = cv2.warpAffine(img, M, (rows, cols))
# 傅里叶变换
dft3 = cv2.dft(np.float32(rot), flags=cv2.DFT_COMPLEX_OUTPUT)
dft_shift3 = np.fft.fftshift(dft3)
res3 = 20 * np.log(cv2.magnitude(dft_shift3[:, :, 0], dft_shift3[:, :, 1]))
# 傅里叶逆变换
ishift3 = np.fft.ifftshift(dft_shift3)
iimg3 = cv2.idft(ishift3)
res4 = cv2.magnitude(iimg3[:, :, 0], iimg3[:, :, 1])
# 图像向右平移
H = np.float32([[1, 0, 200], [0, 1, 0]])
tra = cv2.warpAffine(img, H, (rows, cols))
# 傅里叶变换
dft2 = cv2.dft(np.float32(tra), flags=cv2.DFT_COMPLEX_OUTPUT)
dft_shift2 = np.fft.fftshift(dft2)
res5 = 20 * np.log(cv2.magnitude(dft_shift2[:, :, 0], dft_shift2[:, :, 1]))
# 傅里叶逆变换
ishift2 = np.fft.ifftshift(dft_shift2)
iimg2 = cv2.idft(ishift2)
res6 = cv2.magnitude(iimg2[:, :, 0], iimg2[:, :, 1])
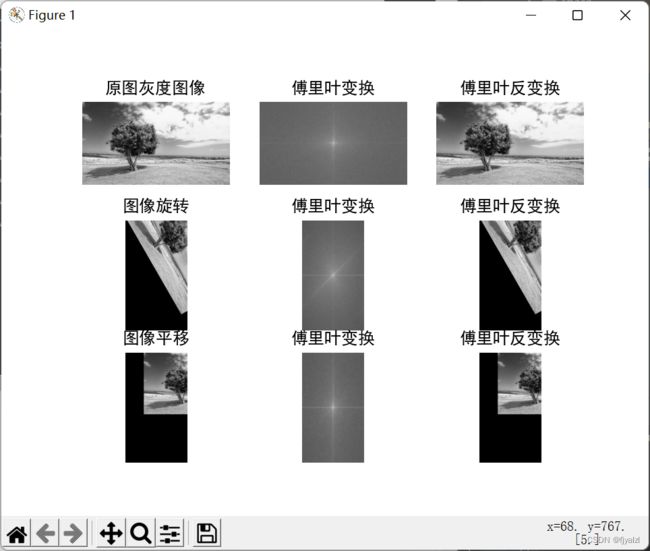
# 输出结果
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.subplot(331), plt.imshow(img, plt.cm.gray), plt.title('原图灰度图像'),plt.axis('off')
plt.subplot(332),plt.imshow(res1,plt.cm.gray),plt.title('傅里叶变换'),plt.axis('off')
plt.subplot(333),plt.imshow(res2,plt.cm.gray),plt.title('傅里叶反变换'),plt.axis('off')
plt.subplot(334),plt.imshow(rot,plt.cm.gray),plt.title('图像旋转'),plt.axis('off')
plt.subplot(335),plt.imshow(res3,plt.cm.gray),plt.title('傅里叶变换'),plt.axis('off')
plt.subplot(336),plt.imshow(res4,plt.cm.gray),plt.title('傅里叶反变换'),plt.axis('off')
plt.subplot(337),plt.imshow(tra,plt.cm.gray),plt.title('图像平移'),plt.axis('off')
plt.subplot(338),plt.imshow(res5,plt.cm.gray),plt.title('傅里叶变换'),plt.axis('off')
plt.subplot(339),plt.imshow(res6,plt.cm.gray),plt.title('傅里叶反变换'),plt.axis('off')
# plt.savefig('1.new.jpg')
plt.show()
# 处理函数,要传入路径
put(r'G:\4.png')
4.6 频率域滤波基础
4.6.1 频率域滤波基础
频率域滤波由修改一幅图像的傅里叶变换然后计算其反变换得到处理后的结果组成。由此,给定一幅大小为MxN的数字图像,则感兴趣的基本滤波公式有如下形式:
其中,![]() 是IDFT,F(u,v)是输入图像f(x,y)的DFT,H(u,v)是滤波函数(滤波器、传递函数),g(x,y)是滤波后的(输出)图像。函数F,H和g是大小与输入图像相同的MxN阵列。
是IDFT,F(u,v)是输入图像f(x,y)的DFT,H(u,v)是滤波函数(滤波器、传递函数),g(x,y)是滤波后的(输出)图像。函数F,H和g是大小与输入图像相同的MxN阵列。
我们认为衰减高频而通过低频的滤波器H(u,v)(近似称为低通滤波器)将模糊一幅图像,具有相反特性的滤波器(称为高通滤波器)将增强尖锐的细节,但是将导致图像对比度的降低。对滤波器加上一个小常数不会影响尖锐性,但是它的确能防止直流项的消除,并保留色调。
4.6.2 频率域滤波步骤小结
1.给定一幅大小为MxN的输入图像f(x,y),可得到填充参数P和Q。典型地,我们选择P=2M和Q=2N。 2、对f(x,y)添加必要数量的0,形成大小为P×Q的填充图像fp(x,y)
3、用(-1)^(x+y)乘以fp(x,y),移到其变换中心。
4、计算步骤3中图像的离散傅里叶变换(DFT),得到F(u,v)
5、生成一个滤波函数H(u,v),其大小为P×Q,中心在图像中心处。用阵列相乘形成乘积
G(u,v)=H(u,v)F(u,v)。
6、得到处理后的图像:进行傅里叶逆变换,且只选择实部,得到gp(x,y)
7、从gp(x,y)的左上象限处提取M×N区域,得到最终处理结果g(x,y)。
4.6.3 空间和频率域滤波间的对应
空间域与频率域滤波间的纽带是卷积定理。给定一个空间滤波器,可以用该空间滤波器的傅里叶正变换得到其频率域表示。相反,遵循其类似的分析和卷积定理,频率域滤波器的反变换,对应空间域的滤波器。两个滤波器形成了傅里叶变换对:
其中,h(x,y)是一个空间滤波器。因为该滤波器可以由频率域滤波器对一个冲激的相应得到,所以h(x,y)有时称为H(u,v)的脉冲响应。还有,因为上式的离散实现中的所有数值都是有限的,这样的滤波器称为有限冲激响应(FIR)滤波器。
以为频率域高斯滤波器:
空间域中相应滤波器由其反变换得到:
(1)他们是一个傅里叶变换对,两个分量都是高斯的和实的函数,这便于分析。同时高斯曲线很直观,并易于操作。 (2)函数表现为互易的。当H(u)有一个较宽的外形时(![]() ),h(x)有较窄的外形,并且,反之亦然。事实上,当值接近无限时,H(u)接近一个常数函数,并且h(x)趋近于一个冲激,这意味着在频率域和空间域都不能滤波。
),h(x)有较窄的外形,并且,反之亦然。事实上,当值接近无限时,H(u)接近一个常数函数,并且h(x)趋近于一个冲激,这意味着在频率域和空间域都不能滤波。
4.7 使用频率表与滤波器平滑图像
这一部分主要介绍频率域中的各种滤波技术,首先是介绍低通滤波器,低通滤波器主要实现对图像进行模糊,主要介绍三种类型的低通滤波器:理想滤波器/巴特沃斯低通滤波器和高斯低通滤波。高通滤波器主要是实现对图像的锐化过程,突出边缘特征
4.7.1 理想低通滤波器
在以原点为圆心、以D0为半径的园内,无衰减地通过所有频率,而在该圆外“切断”所有频率的二维低通滤波器,称为理想低通滤波器(ILPF);它由下面的函数确定:
其中D0是一个正常数,D(u,v)是频率域中点(u,v)与频率域矩形中心的距离,即
滤波结果如图
可以观察到明显的振铃特性。IPLE的模糊和振铃特性可用卷积定理解释。
4.7.2 布特沃斯低通滤波器
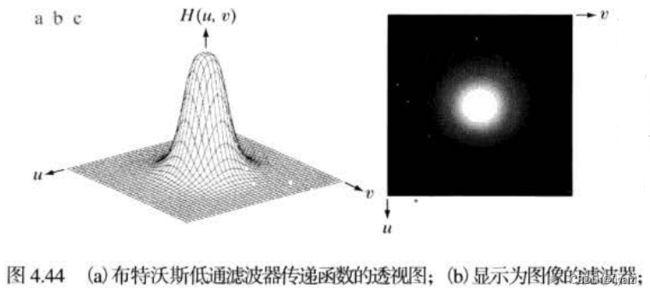
截止频率位于距原点D0处的n阶布特沃斯低通滤波器(BLPF)的传递函数定义为
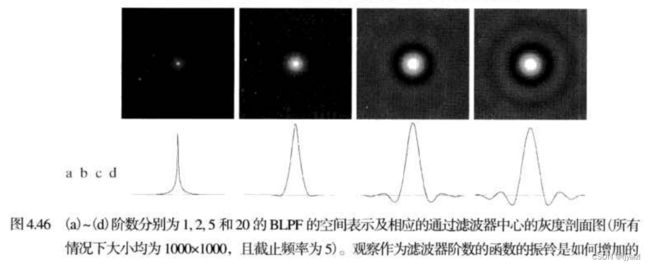
明显可见在黑色白色的边缘过渡平缓, 表现在透视图中0和1的过渡处也是平滑的。滤波结果如下:
图中没有明显的振铃效应。 、
4.7.3 高斯低通滤波器
滤波器的二维形式由下式给出:
高斯低通滤波器(GLPF)的傅里叶反变换也是高斯的,不会产生振铃现象。
4.8 使用频率域滤波器锐化图像
因为边缘和其他灰度的急剧变化与高频分量有关,所以图像的锐化可在频率域通过高通滤波来实现,高通滤波会衰减傅里叶变换中的低频分量而不会扰乱高频信息。
一个高通滤波器是从给定的低通滤波器用下式得到:
![]()
其中HLP(u,v)是低通滤波器的传递函数。也就是说,被低通滤波器衰减的频率能通过高通滤波器,反之亦然。
4.8.1 理想高通滤波器
一个二维理想高通滤波器(IHPF)定义为
其中D0是截止频率。IHPF与ILPF是相对的,在这种情况下,IHPF把以半径为D0的园内的所有频率置零,而毫无衰减地通过圆外的所有频率。如同ILPF那样,IHPF也是物理上无法实现的,IHPF可以用来解释空间域中的振铃等现象。
4.8.2 布特沃斯高通滤波器
截止频率为D0的n阶布特沃斯高通滤波器(BHPF)定义为
4.8.3 高斯高通滤波器
截止频率处在距频率矩形中心距离为D0的高斯高通滤波器(GHPF)的传递函数由下式给出:
4.8.4 频率域的拉普拉斯算子
拉普拉斯算子可使用如下滤波器在频率域实现:
或者,关于频率矩形的中心,使用如下滤波器:
拉普拉斯图像由下式得到:
其中,F(u,v)是f(x,y)的傅里叶变换。增强可使用下式实现:
4.8.5 钝化模板、高提升滤波和高频强调滤波
其中HLP(u,v)是一个低通滤波器,F(u,v)是f(x,y)的傅里叶变换。fLP(x,y)是平滑后的图像。
该表达式定义了k=1时的钝化模板和k>1时的高提升滤波器。我们可以完全使用涉及低通滤波器或高通滤波器的频率域计算来表达上式
高频强调滤波的更一般公式为:
三种滤波器的高通、低通代码实现:
import os
import numpy as np
import cv2
import matplotlib.pyplot as plt
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False
# 理想低通滤波器
def LowPassFilter(img):
"""
理想低通滤波器
"""
# 傅里叶变换
dft = cv2.dft(np.float32(img), flags=cv2.DFT_COMPLEX_OUTPUT)
fshift = np.fft.fftshift(dft)
# 设置低通滤波器
rows, cols = img.shape
crow, ccol = int(rows / 2), int(cols / 2) # 中心位置
mask = np.zeros((rows, cols, 2), np.uint8)
mask[crow - 20:crow + 20, ccol - 20:ccol + 20] = 1
# 掩膜图像和频谱图像乘积
f = fshift * mask
# 傅里叶逆变换
ishift = np.fft.ifftshift(f)
iimg = cv2.idft(ishift)
res = cv2.magnitude(iimg[:, :, 0], iimg[:, :, 1])
return res
# 理想高通滤波器
def HighPassFilter(img):
"""
理想高通滤波器
"""
# 傅里叶变换
f = np.fft.fft2(img)
fshift = np.fft.fftshift(f)
# 设置高通滤波器
rows, cols = img.shape
crow, ccol = int(rows / 2), int(cols / 2)
fshift[crow - 2:crow + 2, ccol - 2:ccol + 2] = 0
# 傅里叶逆变换
ishift = np.fft.ifftshift(fshift)
iimg = np.fft.ifft2(ishift)
iimg = np.abs(iimg)
return iimg
# 巴特沃斯低通滤波器
def ButterworthLowPassFilter(image, d, n, s1):
"""
Butterworth低通滤波器
"""
f = np.fft.fft2(image)
fshift = np.fft.fftshift(f)
def make_transform_matrix(d):
transform_matrix = np.zeros(image.shape)
center_point = tuple(map(lambda x: (x - 1) / 2, s1.shape))
for i in range(transform_matrix.shape[0]):
for j in range(transform_matrix.shape[1]):
def cal_distance(pa, pb):
from math import sqrt
dis = sqrt((pa[0] - pb[0]) ** 2 + (pa[1] - pb[1]) ** 2)
return dis
dis = cal_distance(center_point, (i, j))
transform_matrix[i, j] = 1 / (1 + (dis / d) ** (2 * n))
return transform_matrix
d_matrix = make_transform_matrix(d)
new_img = np.abs(np.fft.ifft2(np.fft.ifftshift(fshift * d_matrix)))
return new_img
# 巴特沃斯高通滤波器
def ButterworthHighPassFilter(image, d, n, s1):
"""
Butterworth高通滤波器
"""
f = np.fft.fft2(image)
fshift = np.fft.fftshift(f)
def make_transform_matrix(d):
transform_matrix = np.zeros(image.shape)
center_point = tuple(map(lambda x: (x - 1) / 2, s1.shape))
for i in range(transform_matrix.shape[0]):
for j in range(transform_matrix.shape[1]):
def cal_distance(pa, pb):
from math import sqrt
dis = sqrt((pa[0] - pb[0]) ** 2 + (pa[1] - pb[1]) ** 2)
return dis
dis = cal_distance(center_point, (i, j))
transform_matrix[i, j] = 1 / (1 + (d / dis) ** (2 * n))
return transform_matrix
d_matrix = make_transform_matrix(d)
new_img = np.abs(np.fft.ifft2(np.fft.ifftshift(fshift * d_matrix)))
return new_img
# 指数滤波器
def filter(img, D0, W=None, N=2, type='lp', filter='exponential'):
'''
频域滤波器
Args:
img: 灰度图片
D0: 截止频率
W: 带宽
N: butterworth和指数滤波器的阶数
type: lp, hp, bp, bs即低通、高通、带通、带阻
Returns:
imgback:滤波后的图像
'''
# 离散傅里叶变换
dft = cv2.dft(np.float32(img), flags=cv2.DFT_COMPLEX_OUTPUT)
# 中心化
dtf_shift = np.fft.fftshift(dft)
rows, cols = img.shape
crow, ccol = int(rows / 2), int(cols / 2) # 计算频谱中心
mask = np.ones((rows, cols, 2)) # 生成rows行cols列的2纬矩阵
for i in range(rows):
for j in range(cols):
D = np.sqrt((i - crow) ** 2 + (j - ccol) ** 2)
if (filter.lower() == 'exponential'): # 指数滤波器
if (type == 'lp'):
mask[i, j] = np.exp(-(D / D0) ** (2 * N))
elif (type == 'hp'):
mask[i, j] = np.exp(-(D0 / D) ** (2 * N))
elif (type == 'bs'):
mask[i, j] = np.exp(-(D * W / (D ** 2 - D0 ** 2)) ** (2 * N))
elif (type == 'bp'):
mask[i, j] = np.exp(-((D ** 2 - D0 ** 2) / D * W) ** (2 * N))
else:
assert ('type error')
fshift = dtf_shift * mask
f_ishift = np.fft.ifftshift(fshift)
img_back = cv2.idft(f_ishift)
img_back = cv2.magnitude(img_back[:, :, 0], img_back[:, :, 1]) # 计算像素梯度的绝对值
img_back = np.abs(img_back)
img_back = (img_back - np.amin(img_back)) / (np.amax(img_back) - np.amin(img_back))
return img_back
def put(path):
img = cv2.imread(path, 1)
# img = cv2.imread(os.path.join(base, path), 1)
img = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY)
f = np.fft.fft2(img)
fshift = np.fft.fftshift(f)
# 取绝对值后将复数变化为实数 # 取对数的目的是将数据变换到0~255
s1 = np.log(np.abs(fshift))
# 用以中文显示
plt.subplot(331)
plt.axis('off')
plt.title('原始图像')
plt.imshow(img, cmap='gray')
plt.subplot(332)
plt.axis('off')
plt.title('理想低通20')
res1 = LowPassFilter(img)
plt.imshow(res1, cmap='gray')
plt.subplot(333)
plt.axis('off')
plt.title('理想高通2')
res2 = HighPassFilter(img)
plt.imshow(res2, cmap='gray')
plt.subplot(334)
plt.axis('off')
plt.title('原始图像')
plt.imshow(img, cmap='gray')
plt.subplot(335)
plt.axis('off')
plt.title('巴特沃斯低通20')
butter_10_1 = ButterworthLowPassFilter(img, 20, 1, s1)
plt.imshow(butter_10_1, cmap='gray')
plt.subplot(336)
plt.axis('off')
plt.title('巴特沃斯高通2')
butter_2_1_1 = ButterworthHighPassFilter(img, 2, 1, s1)
plt.imshow(butter_2_1_1, cmap='gray')
plt.subplot(337)
plt.axis('off')
plt.title('指数原始图像')
plt.imshow(img, cmap='gray')
plt.subplot(338)
plt.axis('off')
plt.title('指数低通图像20')
img_back = filter(img, 30, type='lp')
plt.imshow(img_back, cmap='gray')
plt.subplot(339)
plt.axis('off')
plt.title('指数高通图像2')
img_back = filter(img, 2, type='hp')
plt.imshow(img_back, cmap='gray')
# plt.savefig('2.new.jpg')
plt.show()
# 处理函数,要传入路径
put(r'G:\4.png')
4.9 选择性滤波
第一类滤波器分别称为带阻滤波器或带通滤波器。第二类滤波器称为陷波滤波器。
4.9.1 带阻滤波器和带通滤波器
下面给出了理想、布特沃斯和高斯带阻滤波器的表达式,以及高斯带通滤波器的图像形式:
4.9.2 陷波滤波器
一般形式
对于每个滤波器,距离的计算由下式执行:
![]()