Bishop 模式识别与机器学习读书笔记_ch3.2 线性回归(II)
ch3.2 岭回归与局部线性回归
0. 简单回顾
由上一节课可知,线性回归的目标函数为
min w E ( w ) = ( t − X w ) T ( t − X w ) (1) \min_w \;E(\boldsymbol{w})=(\boldsymbol{t}-\boldsymbol{X}\boldsymbol{w})^T(\boldsymbol{t}-\boldsymbol{X}\boldsymbol{w})\tag{1} wminE(w)=(t−Xw)T(t−Xw)(1)
当 X T X \boldsymbol{X}^T\boldsymbol{X} XTX 可逆时,问题的最优解为
w ^ = ( X T X ) − 1 X T t \hat{w}=(\boldsymbol{X}^T\boldsymbol{X})^{-1}\boldsymbol{X}^T\boldsymbol{t} w^=(XTX)−1XTt
现在的问题是,我们并不能保证矩阵 X T X \boldsymbol{X}^T\boldsymbol{X} XTX 是可逆矩阵, X T X \boldsymbol{X}^T\boldsymbol{X} XTX 为半正定矩阵而不一定是正定矩阵,因为,对于任意非零向量 u \mathbf{u} u,
u T X T X u = ( X u ) T ( X u ) ≥ 0 \mathbf{u}^T\boldsymbol{X}^T\boldsymbol{X}\mathbf{u}=(\boldsymbol{X}\mathbf{u})^T(\boldsymbol{X}\mathbf{u})\geq 0 uTXTXu=(Xu)T(Xu)≥0
为了保证该矩阵是正定矩阵,我们不妨给其加入一个扰动项 λ ⋅ I \lambda\cdot\mathbf{I} λ⋅I, 即对于任意非零向量 u \mathbf{u} u,
u T ( X T X + λ ⋅ I ) u = ( X u ) T ( X u ) + λ u T u > 0 \mathbf{u}^T\Big(\boldsymbol{X}^T\boldsymbol{X}+\lambda\cdot\mathbf{I}\Big)\mathbf{u}=(\boldsymbol{X}\mathbf{u})^T(\boldsymbol{X}\mathbf{u})+\lambda\mathbf{u}^T\mathbf{u}> 0 uT(XTX+λ⋅I)u=(Xu)T(Xu)+λuTu>0
即矩阵 X T X + λ ⋅ I \boldsymbol{X}^T\boldsymbol{X}+\lambda\cdot\mathbf{I} XTX+λ⋅I 为正定矩阵,从而保证了其一定是可逆矩阵,也就保证了回归方程是有意义的。
扰动项的加入是否是无意义的建模过程?
1. 正则化技术
正则指的是一种边界限制条件,这种限制边界条件的技术称为正则化技术。由于回归问题的解是 w \boldsymbol{w} w, 则边界限制条件指的是对 w \boldsymbol{w} w 的边界限定,而非对数据 x \boldsymbol{x} x 的边界限定。
常见的边界限制条件有1-范数、2-范数
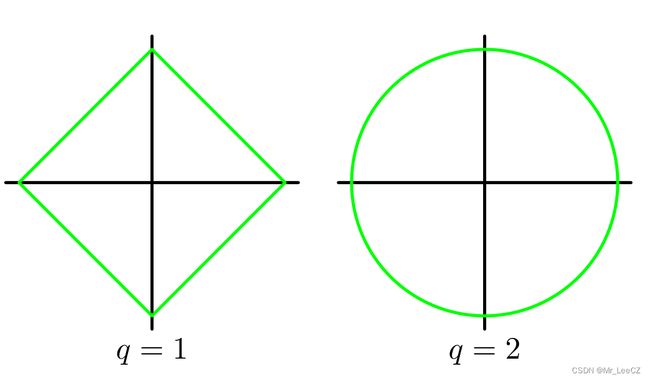
∥ w ∥ 2 = ( w T w ) 1 / 2 = ( w 1 2 + w 2 2 + ⋯ + w n 2 ) 1 / 2 ∥ w ∥ 1 = ∣ w 1 ∣ + ∣ w 2 ∣ + ⋯ + ∣ w n ∣ \begin{align}\Vert\boldsymbol{w}\Vert_2&=(\boldsymbol{w}^T\boldsymbol{w})^{1/2}=(w_1^2+w_2^2+\cdots+w_n^2)^{1/2} \\ \Vert\boldsymbol{w}\Vert_1&=\vert w_1\vert+\vert w_2\vert+\cdots+\vert w_n\vert \end{align} ∥w∥2∥w∥1=(wTw)1/2=(w12+w22+⋯+wn2)1/2=∣w1∣+∣w2∣+⋯+∣wn∣
如图所示,给出了 ∥ w ∥ 2 = R \Vert\boldsymbol{w}\Vert_2=R ∥w∥2=R 和 ∥ w ∥ 2 = R \Vert\boldsymbol{w}\Vert_2=R ∥w∥2=R 两种情况的边界。
对多元回归的目标函数(1)增加一个边界限制条件,表示为
min w E ( w ) = ( t − X w ) T ( t − X w ) s . t . ∥ w ∥ q = R (2) \begin{align}\min_w \;E(\boldsymbol{w})=(\boldsymbol{t}-\boldsymbol{X}\boldsymbol{w})^T(\boldsymbol{t}-\boldsymbol{X}\boldsymbol{w})\\ s.t.\;\;\;\;\;\;\;\;\; \Vert\boldsymbol{w}\Vert_q=R \;\;\;\;\;\;\;\;\;\;\;\;\;\;\; \end{align}\tag{2} wminE(w)=(t−Xw)T(t−Xw)s.t.∥w∥q=R(2)
2. 岭回归
在公式(2)中令 q = 2 q=2 q=2,有
min w E ( w ) = ( t − X w ) T ( t − X w ) s . t . ∥ w ∥ 2 = R (3) \begin{align}\min_w \;E(\boldsymbol{w})=(\boldsymbol{t}-\boldsymbol{X}\boldsymbol{w})^T(\boldsymbol{t}-\boldsymbol{X}\boldsymbol{w})\\ s.t.\;\;\;\;\;\;\;\;\; \Vert\boldsymbol{w}\Vert_2=R \;\;\;\;\;\;\;\;\;\;\;\;\;\;\; \end{align}\tag{3} wminE(w)=(t−Xw)T(t−Xw)s.t.∥w∥2=R(3)
公式(3)的求解可利用拉格朗日乘子法将约束优化问题转化为无约束优化问题
E ( w ) = ( t − X w ) T ( t − X w ) + λ ( ∥ w ∥ 2 2 − R 2 ) E(\boldsymbol{w})=(\boldsymbol{t}-\boldsymbol{X}\boldsymbol{w})^T(\boldsymbol{t}-\boldsymbol{X}\boldsymbol{w})+\lambda(\Vert\boldsymbol{w}\Vert_2^2-R^2) E(w)=(t−Xw)T(t−Xw)+λ(∥w∥22−R2)
其优化函数等价于
E ( w ) = ( t − X w ) T ( t − X w ) + λ ∥ w ∥ 2 2 (4) E(\boldsymbol{w})=(\boldsymbol{t}-\boldsymbol{X}\boldsymbol{w})^T(\boldsymbol{t}-\boldsymbol{X}\boldsymbol{w})+\lambda\Vert\boldsymbol{w}\Vert_2^2\tag{4} E(w)=(t−Xw)T(t−Xw)+λ∥w∥22(4)
公式(4)加了2-范数正则化的回归问题称为岭回归。其优化解的过程为
∂ E ( w ) ∂ w = − 2 X T ( t − X w ) + 2 λ w = 0 \frac{\partial E(\boldsymbol{w})}{\partial \boldsymbol{w}}=-2\boldsymbol{X}^T(\boldsymbol{t}-\boldsymbol{X}\boldsymbol{w})+2\lambda\boldsymbol{w}=0 ∂w∂E(w)=−2XT(t−Xw)+2λw=0
得
w ^ = ( X T X + λ ⋅ I ) − 1 X T t \hat{w}=(\boldsymbol{X}^T\boldsymbol{X}+\lambda\cdot\mathbf{I})^{-1}\boldsymbol{X}^T\boldsymbol{t} w^=(XTX+λ⋅I)−1XTt
此优化解与避免矩阵不可逆得设想是一致的。
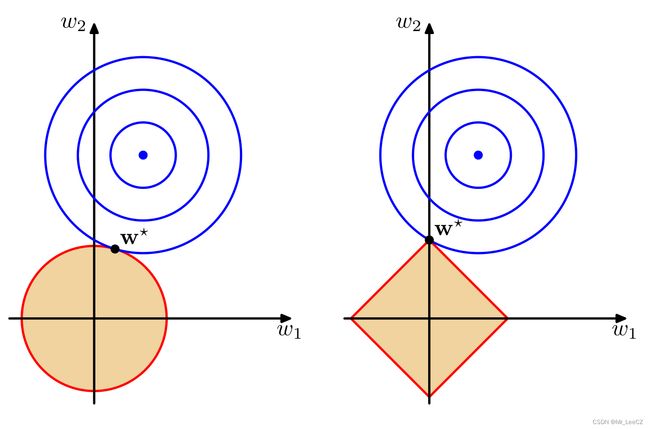
由公式(3)和公式(4)相比,我们发现限制半径 R R R 是不影响最优解的,简单起见,不妨设置 R = 1 R=1 R=1. 岭回归和原优化问题模型相比具有一定的优势,这种优势可通过图进行认识。
3. 岭回归模型的推广
将公式(4)中的范数修正为1范数,则目标函数变为
E ( w ) = ( t − X w ) T ( t − X w ) + λ ∥ w ∥ 1 (5) E(\boldsymbol{w})=(\boldsymbol{t}-\boldsymbol{X}\boldsymbol{w})^T(\boldsymbol{t}-\boldsymbol{X}\boldsymbol{w})+\lambda\Vert\boldsymbol{w}\Vert_1\tag{5} E(w)=(t−Xw)T(t−Xw)+λ∥w∥1(5)
公式(5)这种算法称为Lasso回归。Lasso回归的最大优势可以做特征的筛选。
将公式(4)中的范数修正为1-范数和2-范数的组合,则目标函数变为
E ( w ) = ( t − X w ) T ( t − X w ) + α ∥ w ∥ 1 + β ∥ w ∥ 2 (6) E(\boldsymbol{w})=(\boldsymbol{t}-\boldsymbol{X}\boldsymbol{w})^T(\boldsymbol{t}-\boldsymbol{X}\boldsymbol{w})+\alpha\Vert\boldsymbol{w}\Vert_1+\beta\Vert\boldsymbol{w}\Vert_2\tag{6} E(w)=(t−Xw)T(t−Xw)+α∥w∥1+β∥w∥2(6)
公式(5)这种算法称为弹性网回归。
4. 算法的实现
#!/usr/bin/python
# -*- coding:utf-8 -*-
import numpy as np
from sklearn.linear_model import LinearRegression, RidgeCV, LassoCV, ElasticNetCV
from sklearn.preprocessing import PolynomialFeatures
from sklearn.pipeline import Pipeline
from sklearn.exceptions import ConvergenceWarning
import matplotlib as mpl
import matplotlib.pyplot as plt
import warnings
# import seaborn
def xss(y, y_hat):
y = y.ravel()
y_hat = y_hat.ravel()
# Version 1
tss = ((y - np.average(y)) ** 2).sum()
rss = ((y_hat - y) ** 2).sum()
ess = ((y_hat - np.average(y)) ** 2).sum()
r2 = 1 - rss / tss
# print 'RSS:', rss, '\t ESS:', ess
# print 'TSS:', tss, 'RSS + ESS = ', rss + ess
tss_list.append(tss)
rss_list.append(rss)
ess_list.append(ess)
ess_rss_list.append(rss + ess)
# Version 2
# tss = np.var(y)
# rss = np.average((y_hat - y) ** 2)
# r2 = 1 - rss / tss
corr_coef = np.corrcoef(y, y_hat)[0, 1]
return r2, corr_coef
if __name__ == "__main__":
warnings.filterwarnings(action='ignore', category=ConvergenceWarning)
np.random.seed(0)
np.set_printoptions(linewidth=300, suppress=True)
N = 9
x = np.linspace(0, 6, N) + np.random.randn(N)
x = np.sort(x)
y = x**2 - 4*x - 3 + np.random.randn(N)
x.shape = -1, 1
y.shape = -1, 1
models = [Pipeline([
('poly', PolynomialFeatures()),
('linear', LinearRegression(fit_intercept=False))]),
Pipeline([
('poly', PolynomialFeatures()),
('linear', RidgeCV(alphas=np.logspace(-3, 2, 10), fit_intercept=False))]),
Pipeline([
('poly', PolynomialFeatures()),
('linear', LassoCV(alphas=np.logspace(-3, 2, 10), fit_intercept=False))]),
Pipeline([
('poly', PolynomialFeatures()),
('linear', ElasticNetCV(alphas=np.logspace(-3, 2, 10), l1_ratio=[.1, .5, .7, .9, .95, .99, 1],
fit_intercept=False))])
]
mpl.rcParams['font.sans-serif'] = ['simHei']
mpl.rcParams['axes.unicode_minus'] = False
plt.figure(figsize=(15, 10), facecolor='w')
d_pool = np.arange(1, N, 1) # 阶
m = d_pool.size
clrs = [] # 颜色
for c in np.linspace(16711680, 255, m, dtype=int):
clrs.append('#%06x' % c)
line_width = np.linspace(5, 2, m)
titles = '线性回归', 'Ridge回归', 'LASSO', 'ElasticNet'
tss_list = []
rss_list = []
ess_list = []
ess_rss_list = []
for t in range(4):
model = models[t]
plt.subplot(2, 2, t+1)
plt.plot(x, y, 'ro', markersize=10, zorder=N, mec='k')
for i, d in enumerate(d_pool):
model.set_params(poly__degree=d)
model.fit(x, y.ravel())
lin = model.get_params('linear')['linear']
output = '%s:%d阶,系数为:' % (titles[t], d)
if hasattr(lin, 'alpha_'):
idx = output.find('系数')
output = output[:idx] + ('alpha=%.6f,' % lin.alpha_) + output[idx:]
if hasattr(lin, 'l1_ratio_'): # 根据交叉验证结果,从输入l1_ratio(list)中选择的最优l1_ratio_(float)
idx = output.find('系数')
output = output[:idx] + ('l1_ratio=%.6f,' % lin.l1_ratio_) + output[idx:]
print(output, lin.coef_.ravel())
x_hat = np.linspace(x.min(), x.max(), num=100)
x_hat.shape = -1, 1
y_hat = model.predict(x_hat)
s = model.score(x, y)
r2, corr_coef = xss(y, model.predict(x))
# print 'R2和相关系数:', r2, corr_coef
# print 'R2:', s, '\n'
z = N - 1 if (d == 2) else 0
label = '%d阶,$R^2$=%.3f' % (d, s)
if hasattr(lin, 'l1_ratio_'):
label += ',L1 ratio=%.2f' % lin.l1_ratio_
plt.plot(x_hat, y_hat, color=clrs[i], lw=line_width[i], alpha=0.75, label=label, zorder=z)
plt.legend(loc='upper left')
plt.grid(True)
plt.title(titles[t], fontsize=18)
plt.xlabel('X', fontsize=16)
plt.ylabel('Y', fontsize=16)
plt.tight_layout(1, rect=(0, 0, 1, 0.95))
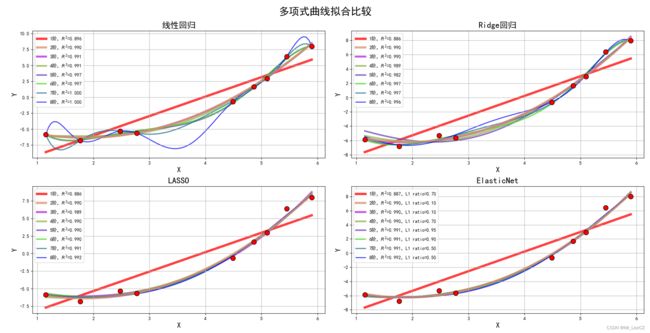
plt.suptitle('多项式曲线拟合比较', fontsize=22)
plt.show()
y_max = max(max(tss_list), max(ess_rss_list)) * 1.05
plt.figure(figsize=(9, 7), facecolor='w')
t = np.arange(len(tss_list))
plt.plot(t, tss_list, 'ro-', lw=2, label='TSS(Total Sum of Squares)', mec='k')
plt.plot(t, ess_list, 'mo-', lw=1, label='ESS(Explained Sum of Squares)', mec='k')
plt.plot(t, rss_list, 'bo-', lw=1, label='RSS(Residual Sum of Squares)', mec='k')
plt.plot(t, ess_rss_list, 'go-', lw=2, label='ESS+RSS', mec='k')
plt.ylim((0, y_max))
plt.legend(loc='center right')
plt.xlabel('实验:线性回归/Ridge/LASSO/Elastic Net', fontsize=15)
plt.ylabel('XSS值', fontsize=15)
plt.title('总平方和TSS=?', fontsize=18)
plt.grid(True)
plt.show()
结果为
线性回归:1阶,系数为: [-12.12113792 3.05477422]
线性回归:2阶,系数为: [-3.23812184 -3.36390661 0.90493645]
线性回归:3阶,系数为: [-3.90207326 -2.61163034 0.66422328 0.02290431]
线性回归:4阶,系数为: [-8.20599769 4.20778207 -2.85304163 0.73902338 -0.05008557]
线性回归:5阶,系数为: [ 21.59733285 -54.12232017 38.43116219 -12.68651476 1.98134176 -0.11572371]
线性回归:6阶,系数为: [ 14.73304785 -37.87317494 23.67462342 -6.07037979 0.42536833 0.06803132 -0.00859246]
线性回归:7阶,系数为: [ 314.30344622 -827.89446924 857.33293186 -465.46543638 144.21883851 -25.67294678 2.44658612 -0.09675941]
线性回归:8阶,系数为: [-1189.50149198 3643.69109456 -4647.92941149 3217.22814712 -1325.87384337 334.32869072 -50.57119119 4.21251817 -0.148521 ]
Ridge回归:1阶,alpha=0.166810,系数为: [-10.79755177 2.75712205]
Ridge回归:2阶,alpha=0.166810,系数为: [-2.86616277 -3.50791358 0.918189 ]
Ridge回归:3阶,alpha=0.046416,系数为: [-3.54779374 -2.8374223 0.70197829 0.02141529]
Ridge回归:4阶,alpha=0.166810,系数为: [-3.04995117 -2.03455252 -0.27692755 0.29868134 -0.02333296]
Ridge回归:5阶,alpha=0.599484,系数为: [-2.11991122 -1.79172368 -0.80325245 0.40787788 -0.02053857 -0.00138782]
Ridge回归:6阶,alpha=0.001000,系数为: [ 0.53724068 -6.00552086 -3.75961826 5.64559118 -2.21569695 0.36872912 -0.02221332]
Ridge回归:7阶,alpha=0.046416,系数为: [-2.3505499 -2.24317832 -1.48682673 -0.01259016 1.13568801 -0.53064855 0.09225692 -0.0056092 ]
Ridge回归:8阶,alpha=0.166810,系数为: [-2.12001325 -1.87286852 -1.21783635 -0.23911648 0.46196438 0.10072047 -0.11365043 0.02363435 -0.00153598]
LASSO:1阶,alpha=0.166810,系数为: [-10.83995051 2.75973604]
LASSO:2阶,alpha=0.001000,系数为: [-3.29932625 -3.31989869 0.89878903]
LASSO:3阶,alpha=0.046416,系数为: [-4.64384442 -1.41251028 0.21902411 0.06870173]
LASSO:4阶,alpha=0.001000,系数为: [-5.10441283 -1.40548737 0.34041047 0.04314629 0.00106782]
LASSO:5阶,alpha=0.046416,系数为: [-4.06779799 -1.87958288 0.25392724 0.08205579 0.00254474 -0.00071398]
LASSO:6阶,alpha=0.046416,系数为: [-3.79737378 -1.94437059 0.19659912 0.08388358 0.00493576 -0.00008277 -0.00013701]
LASSO:7阶,alpha=0.001000,系数为: [-4.51456835 -1.58477275 0.23483228 0.04900369 0.00593868 0.00044879 -0.00002625 -0.00002132]
LASSO:8阶,alpha=0.001000,系数为: [-4.62623251 -1.37717809 0.17183854 0.04307765 0.00629505 0.00069171 0.0000355 -0.00000875 -0.00000386]
ElasticNet:1阶,alpha=0.046416,l1_ratio=0.700000,系数为: [-10.86769313 2.77155741]
ElasticNet:2阶,alpha=0.012915,l1_ratio=0.100000,系数为: [-2.95636027 -3.48289871 0.91690773]
ElasticNet:3阶,alpha=0.003594,l1_ratio=0.100000,系数为: [-4.46002272 -1.862843 0.404499 0.04874065]
ElasticNet:4阶,alpha=0.003594,l1_ratio=0.700000,系数为: [-4.84733559 -1.60507006 0.37733372 0.04381132 0.00064991]
ElasticNet:5阶,alpha=0.012915,l1_ratio=0.950000,系数为: [-4.4414985 -1.82324855 0.34615981 0.05815521 0.00274446 -0.00050502]
ElasticNet:6阶,alpha=0.012915,l1_ratio=0.900000,系数为: [-4.11634148 -1.95714891 0.31374451 0.05953931 0.00467125 0.0000186 -0.00011516]
ElasticNet:7阶,alpha=0.001000,l1_ratio=0.500000,系数为: [-4.42582081 -1.65931193 0.25094663 0.04866323 0.00584375 0.00044071 -0.00002632 -0.00002118]
ElasticNet:8阶,alpha=0.001000,l1_ratio=0.500000,系数为: [-4.53761647 -1.45230301 0.18829714 0.0427561 0.00619739 0.00068209 0.00003506 -0.00000869 -0.00000384]
5. 小结
- 过拟合一般是由模型复杂度高或者数据量少造成的,而这两种因素本质上是一致的;
- 正则化技术是消除过拟合的一种有效手段,降低了模型复杂度(筛选了特征,排除掉无关特征)