自己动手写数据结构（11）——二叉排序树

自己动手写数据结构总目录

具体内容：

• 1.链表

• 2.栈和队列及其应用

• 3.串

• 4.二叉树

• 5.树

• 6.图及其五种存储方式

• 7.图的最小生成树

• 8.图的最短路径

• 9.图的拓扑排序和关键路径

• 10.有序表查找（详解斐波那契查找）

• 11.二叉排序树

• 12.平衡二叉树（详解结点删除）

该文章的源代码仓库为：https://github.com/MeteorCh/DataStructure/blob/master/Java/DataStructure/src/Searching/BinarySortingTree/BinarySortingTree.java
上一篇博客写了有序表查找，其中三种方法的基本思想都是二分查找，他们的查找的时间复杂度均为 O(logn)，我们发现有序表的查找效率挺高的了，但是插入效率很低，插入的时间复杂度仍然是O(n)，为了提高插入效率，有人提出了二叉排序树的数据结构。

一、定义

二叉排序树，又称二叉查找树。它或者是一颗空树，或者是一棵具有下列性质的二叉树：

• 若它的左子树不空，则左子树上所有结点的值均小于它的根节点的值；
• 若它的右子树不空，则右子树上所有节点的值均大于它的根节点的值；
• 它的左、右子树也分别是二叉排序树。
  上面的定义是一种二叉树中常见的递归的定义方法。这种二叉排序树左子树节点一定比父节点小，右子树节点一定比双亲节点大。如下面就是一颗二叉排序树：
  

二、二叉排序树的操作

1.查找

二叉排序树的查找其实很好理解，给定一个键值key，从根节点开始，比较当前节点的键值与key的大小，如果大于key，则在该节点的右子树中查找；如果小于key，则在该节点的左子树中查找，不断递归，直到找到或者到达叶子节点（未找到）。比如上面的二叉排序树中，查找51，查找过程为：

二叉排序树查找的时间复杂度是O(logn)。

2.插入

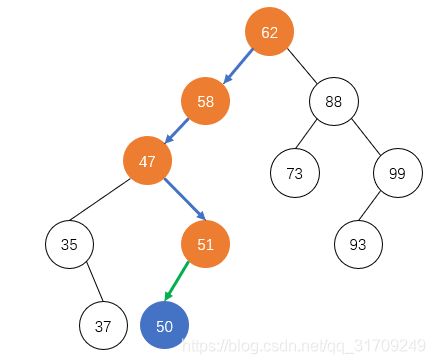
有了查找，插入就非常容易了。对于一个要插入的key，先按照上面的查找算法，直到找到叶子结点。再去判断key与该叶子结点的大小关系，如果key大于叶子结点，则key结点作为叶子结点的右孩子，小于的话则作为叶子结点的左孩子。比如上面的二叉排序树插入50，我们先查找到51所在的节点，然后将50作为51结点的左孩子。插入过程如下：

3.删除

二叉排序树中结点的删除是最复杂的一种操作。需要分三种情况讨论：

(1)删除结点为叶节点

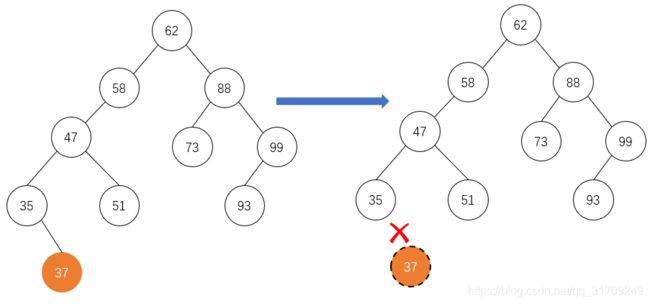
删除节点为叶结点，说明删除结点的左右孩子均为空。这是最简单的一种情况。如下图，我们删除二叉排序树中的37结点。我们只需要找到37的父节点35，将对应的孩子节点置空，然后释放被删除节点即可。

(2)删除结点左孩子或右孩子为空

这是稍微复杂一点的情况。当删除结点node的左孩子为空，右孩子不为空时。我们只需要将node的右孩子节点移动到删除节点的位置，然后断开删除节点的连接关系，再释放被删除结点即可。如上面二叉查找树中的35节点，删除时如下所示：

同理，当删除结点node的右孩子为空，左孩子不为空时。我们只需要将node的左孩子移动到删除节点的位置，然后断开删除节点的连接关系，再释放删除结点即可。我这里就不画图了。

(3)删除结点既有左孩子又有右孩子

这是最复杂的情况。这里我们用先覆盖再删除的方式。 （至于为什么要这样，在讨论部分讨论）。
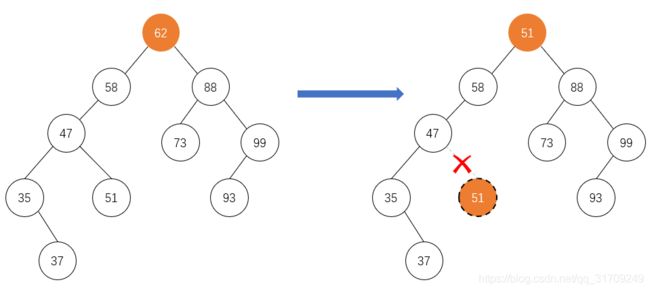
将结点删除后，我们需要找一个树中原来的结点放置在删除位置，那这个结点应该找哪个呢？根据二叉排序树的性质，这个结点要大于左子树中的所有节点，小于右子树中的所有节点。那这个代替节点要么是删除节点左子树中最右边的节点（对应着删除节点左子树中的最大节点），要么是删除节点右子树中最左边的节点（对应着删除节点右子树中的最小节点） 。先覆盖的意思是，将找到的代替节点中的数据全部赋值给删除节点（删除节点的左右孩子、双亲信息不变，只覆盖所携带的数据）。 再删除的意思是再删除代替节点。代替节点的删除肯定是上面两种情况中的一种，调用上面的删除方法即可。 比如删除上面二叉排序树中的根结点62，我们先找到62左子树中最右边的节点51（或者62右子树中最左边的节点73），然后将51节点的键值数据赋值给62节点，再删除51节点。

三、代码实现

用Java实现二叉搜索树如下

/**
 * 二叉排序树
 * 使用示例：
 *          int[] data={62,88,58,47,35,73,51,99,37,93};
 *         BinarySortingTree tree=new BinarySortingTree(data);
 *         tree.find(35);
 *         tree.deleteData(62);
 */
public class BinarySortingTree{

    public static class TreeNode {
        protected int data;//数据
        protected TreeNode lChild,rChild,parent;//左孩子、右孩子、父节点
        public TreeNode(int data){
            this.data=data;
            lChild=rChild=parent=null;
        }
    }

    protected TreeNode root;//根节点
    public BinarySortingTree(){
    }

    public BinarySortingTree(int[] data){//根据传入的数据构建二叉排序树
        for (int i=0;i<data.length;i++){
            insertData(data[i]);
        }
    }

    /**
     * 插入数据
     * @param data
     */
    private void insertData(int data){
        if (root==null){
            //如果根节点为空，给根节点开辟空间
            root=new TreeNode(data);
        }else {
            //如果不是根节点，遍历树得到根节点
            boolean[] flag=new boolean[1];
            flag[0]=false;
            TreeNode insertPos=findInsertPosition(root,data,flag);
            if (flag[0])
                System.out.println("输入的键值重复！");
            else{
                if (insertPos.lChild==null&&insertPos.data>data) {
                    insertPos.lChild=new TreeNode(data);
                    insertPos.lChild.parent=insertPos;
                }
                else if (insertPos.rChild==null&&insertPos.data<data) {
                    insertPos.rChild=new TreeNode(data);
                    insertPos.rChild.parent=insertPos;
                }
            }
        }
    }

    /**
     * 查找data
     * @param data
     * @return
     */
    public void find(int data){
        if (root!=null){
            boolean[] flag=new boolean[1];
            flag[0]=false;
            findInsertPosition(root,data,flag);
            if (flag[0])
                System.out.println("查找的元素"+data+"在数据表中存在");
            else
                System.out.println("查找的元素"+data+"在数据表中不存在");
        }
    }

    /**
     * 查找data的插入位置
     * @param data
     * @return
     */
    protected TreeNode findInsertPosition(TreeNode node,int data,boolean[] flag){
        if (data>node.data)
        {
            if (node.rChild==null)
                return node;
            else
                return findInsertPosition(node.rChild,data,flag);
        }
        else if (data<node.data)
        {
            if (node.lChild==null)
                return node;
            else
                return findInsertPosition(node.lChild,data,flag);
        }
        else{
            flag[0]=true;
            return node;
        }


    }

    /**
     * 提供的对外操作接口
     * @param key
     */
    public void deleteData(int key){
        deleteData(root,key);
    }

    /**
     * 在二叉排序树中删除data元素
     * @param key
     */
    protected void deleteData(TreeNode node,int key){
        if (node==null)
            System.out.println("数据表中不存在"+key);
        else {
            if (key==node.data)
                deleteData(node);
            else if (key<node.data)
                deleteData(node.lChild,key);
            else
                deleteData(node.rChild,key);
        }
    }

    /**
     * 根据节点的左右子树情况来删除节点
     * @param node
     */
    protected void deleteData(TreeNode node){
        if (node.rChild==null||node.lChild==null){//右子树或右子树为空
            TreeNode replacement=node.rChild==null?node.lChild:node.rChild;
            if (node.parent!=null){
                if (node==node.parent.lChild)
                    node.parent.lChild=replacement;
                else if (node==node.parent.rChild)
                    node.parent.rChild=replacement;
                if (replacement!=null)
                    replacement.parent=node.parent;
            }else { //如果node为根节点
                root=replacement;
                replacement.parent=null;
            }
            //清空node释放内存
            node.parent=node.lChild=node.rChild=null;
        }else {//左右子树都不为空
            //找到node的左子树中最右边的叶节点
            TreeNode curNode=node.lChild;
            while (curNode.rChild!=null){
                curNode=curNode.rChild;
            }
            //将curNode的值直接赋值给删除节点
            node.data=curNode.data;
            deleteData(curNode);
        }
    }
}

使用示例如下：

		int[] data={62,88,58,47,35,73,51,99,37,93};
        BinarySortingTree tree=new BinarySortingTree(data);
        tree.find(35);
        tree.deleteData(62);

上面的使用示例就构造了最上面的那棵二叉搜索树。在上面的代码中，我将删除节点的三种情况合并成了两种：左子树或右子树为空（包含两个都空，即叶节点的情况）、左子树右子树均不为空。第一种情况下使用的是直接移动节点到删除节点位置，然后重建连接关系。第二种情况则是采用上面说的先覆盖，再删除的策略。

四、讨论

1.为什么当左右子树不为空的时候，要采用先覆盖再删除的策略？

因为方便。理论上来说，最好的方式应该也是找到替代结点后，将原来要删除的结点释放，再重建替换结点的连接关系，想法很美好，实现起来就很麻烦。比如在我们举例的二叉排序树中，要删除47号结点，那还比较简单，因为37结点是叶结点，我们将37结点与35的连接关系断开，然后将37移动到47位置上即可。但当要删除62号节点，即根节点时，那在它的左子树中找最大的元素，是58结点。当要重建58的连接关系时，就会很麻烦，需要分各种情况讨论。还不如直接曲线救国，先找到替换结点，将替换结点中的数据直接覆盖到删除节点上，但是保持删除节点的左右孩子、父节点等信息，然后替换结点肯定是左孩子或右孩子为空（包含左右孩子均为空的情况），直接用第一种情况做删除，会方便很多。

2.查找插入等的非递归实现？

插入也用到了查找，我上面的代码中查找是利用递归实现的，那非递归应该怎么实现呢。其实很简单，就用一个while循环就可以了，大概代码应该如下所示：

		TreeNode curNode=root;
        while (curNode!=null){
            if (curNode.data==data)
                return curNode;
            else if (curNode.data>data)
                curNode=curNode.lChild;
            else 
                curNode=curNode.rChild;
        }
        if (curNode==null)
            System.out.println("查找元素不存在");

上述代码中，data 为要查找的键值。