Java数据结构（1.1）：数据结构入门+线性表、算法时间复杂度与空间复杂度、线性表、顺序表、单双链表实现、Java线性表、栈、队列、Java栈与队列。

数据结构与算法入门

问题1：为什么要学习数据结构

        

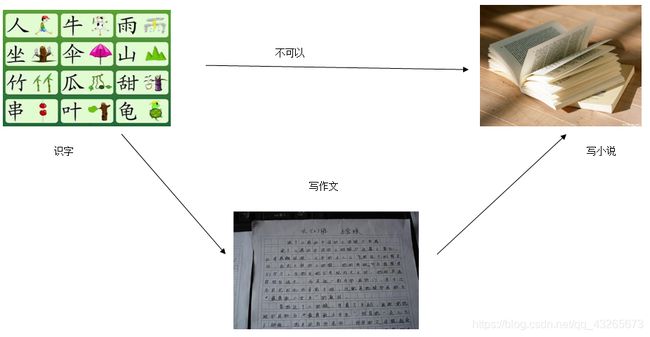
如果说学习语文的最终目的是写小说的话，那么能不能在识字、组词、造句后就直接写小说了，肯定是不行的，

中间还有一个必经的阶段：就是写作文。写作文的直接目的有两个：

1.掌握写作套路、技巧（理论水平），保证以后写小说的质量

2.提高写作水平（动手能力），为以后写小说打好基础

学习一门计算机语言就好比识字阶段，以后开发项目就好比写小说，中间的离不开数据结构的学习，就好比写作文。

         1.高级计算机程序设计的理论指导

                 我塞牙了，那么就要用到牙签这“数据结构”，当然你用指甲也行，只不过“性能”没那么好；

                 我要拧螺母，肯定用扳手这个“数据结构”，当然你用钳子也行，只不过也没那么好用。

                 学习数据结构，就是为了了解以后在IT行业里搬砖需要用到什么工具，这些工具有什么利弊，应用于什么场景。

                 你会发现这些基础的“工具”也存在着一些缺陷，你不满足于此工具，此时，你就开始自己在这些数据结构的基础上加以改造，

                 这就叫做自定义数据结构

                 掌握了开车的本领，桑塔纳、宝马、奔驰、老年代步车都会开。

                 数据结构可以采用不同的语言来描述和实现，此处自然是Java语言

         2.提升编程能力

                 个人认为数据结构是编程最重要的基本功没有之一

                 学习了Java、python、android、C、C++，你就成为编程高手了吗。

                 不见得，每门语言都是入门而已，水平并没有得到多少锻炼

                 学习一门数据结构，掌握了各种简单、复杂数据类型的算法，编程能力就会有大的提升，甚至质的飞跃，内力深厚了。                

         3.面试中经常问到

                 为什么面试官喜欢问数据结构

                 能够看出一个同学是否基础扎实，能够看出一个人的发展后劲

                 因为数据结构本身也有难度           

问题2：有哪些数据结构

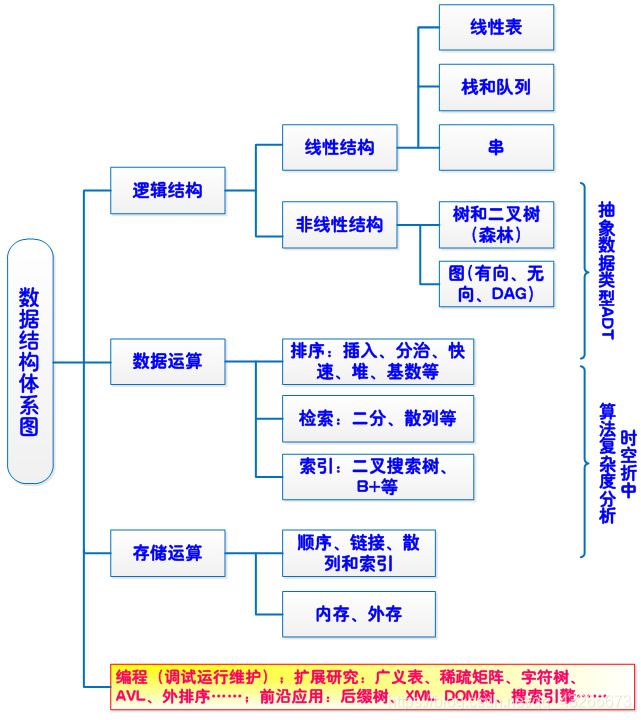
         线性表、栈、队列、（字符）串、数组、广义表、树、二叉树、图

         重点是线性表、二叉树                

         对于每种数据结构会讲解其添加、更新、删除、查询、排序等操作的实现

         数据结构与算法不可分

         对于查询和排序一般单独拿出来讲解

         我们的数据结构要讲解哪些内容

         1.数据结构与算法入门

         2.各种数据结构：线性表、栈、队列、（递归）  树、二叉树、图

         3.查找和排序

问题3：学习数据结构的四种境界

         境界1：听懂理论、听懂算法思路 (理论家、眼高手低，总比不知道强多了)

         境界2：完成主要数据结构基本算法的实现（理论+实践，数据结构入门了）

         境界3：完成更多数据结构更多算法的实现（进步提高数据结构功底）

         境界4：融会贯通、举一反三，在后续开发中综合应用数据结构知识（数据结构就是哲学思想，只要和实践结合才能学好）        

         学习数据结构不是一日之功，对于初学者要达到境界2，后续学习和工作中不断研究学习

基本概念

数据

数据（data） 是描述客观事物的数值、字符以及能输入机器且能被处理的各种符号集合。

数据的含义非常广泛，除了通常的数值数据、字符、字符串是数据以外，声音、图像等一切可以输入计算机并能被处理的都是数据。

例如除了表示人的姓名、身高、体重等的字符、数字是数据，人的照片、指纹、三维模型、语音指令等也都是数据。

数据项

数据项（data item）具有原子性，是不可分割的最小数据单位。

如描述学生相关信息的姓名、性别、学号等都是数据项；

三维坐标中的每一维坐标值也是数据项。数据项具有原子性，是不可分割的最小单位。

数据元素

数据元素（data element ）是数据的基本单位，是数据集合的个体，通常由若干个数据项组成，在计算机程序中通常作为一个整体来进行处理。

例如一条描述一位学生的完整信息的数据记录就是一个数据元素；空间中一点的三维坐标也可以是一个数据元素。

数据对象

数据对象（data object ）是性质相同的数据元素的集合，是数据的子集。

例如一个学校的所有学生的集合就是数据对象，空间中所有点的集合也是数据对象。

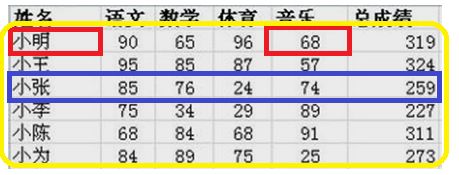
红色：数据项      蓝色：数据元素   黄色：数据对象  

数据结构    （不是建筑结构、人体结构）

数据结构（data structure ）是指相互之间存在一种或多种特定关系的数据元素的集合。

是组织并存储数据以便能够有效使用的一种专门格式，它用来反映一个数据的内部构成，即一个数据由那些成分数据构成，以什么方式构成，呈什么结构。

     

由于信息可以存在于逻辑思维领域，也可以存在于计算机世界，因此作为信息载体的数据同样存在于两个世界中。

表示一组数据元素及其相互关系的数据结构同样也有两种不同的表现形式，

一种是数据结构的逻辑层面，即数据的逻辑结构；

一种是存在于计算机世界的物理层面，即数据的存储结构。

数据结构=逻辑结构+存储结构

数据结构=逻辑结构+存储结构+（在存储结构上的）运算/操作

数据结构类型

数据的逻辑结构

数据的逻辑结构指数据元素之间的逻辑关系（和实现无关）。

分类1：线性结构和非线性结构

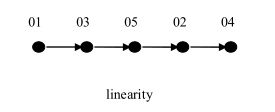
线性结构：有且只有一个开始结点和一个终端结点，并且所有结点都最多只有一个直接前驱和一个直接后继。

线性表就是一个典型的线性结构，它有四个基本特征： 

1．集合中必存在唯一的一个"第一个元素"；

2．集合中必存在唯一的一个"最后的元素"；

3．除最后元素之外，其它数据元素均有唯一的"直接后继"；

4．除第一元素之外，其它数据元素均有唯一的"直接前驱"。

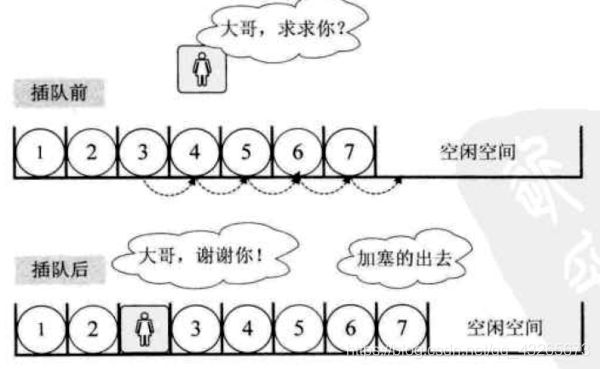
生活案例：冰糖葫芦、 排队上地铁

 

 

相对应于线性结构，非线性结构的逻辑特征是一个结点元素可能对应多个直接前驱和多个直接后继。

常见的非线性结构有：树(二叉树等)，图(网等)。

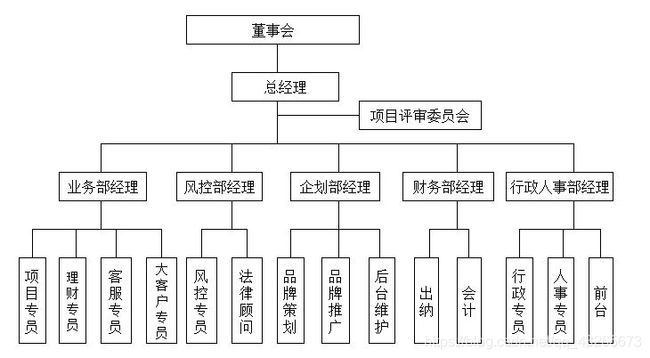
树：

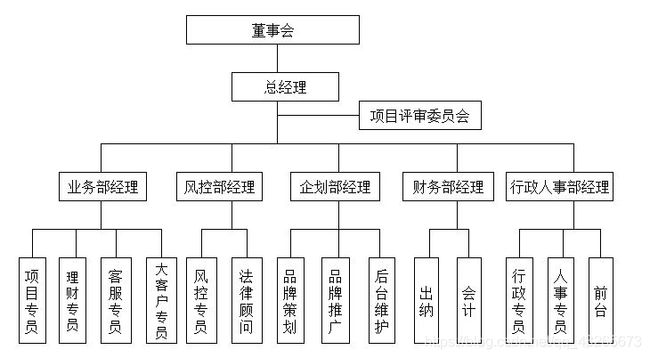
生活案例：单位组织架构、族谱

技术案例：文件系统。

                             

 

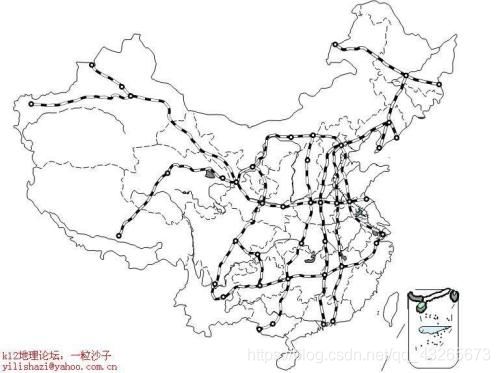
图：

生活案例：交通线路图，地铁图

 

       

 

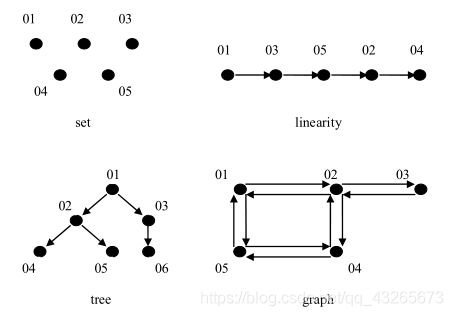
分类2：集合结构 线性结构 树状结构 网络结构

逻辑结构有四种基本类型：集合结构、线性结构、树状结构和网络结构。

表和树是最常用的两种高效数据结构，许多高效的算法能够用这两种数据结构来设计实现。

集合结构：就是数学中所学习的集合。集合中的元素有三个特征：

     1).确定性（集合中的元素必须是确定的）

     2).唯一性（集合中的元素互不相同。例如：集合A={1，a}，则a不能等于1）

     3).无序性（集合中的元素没有先后之分），如集合{3,4,5}和{3,5,4}算作同一个集合

     该结构的数据元素间的关系是“属于同一个集合”，别无其它关系。

     因为集合中元素关系很弱，数据结构中不对该结构进行研究 

线性结构：数据结构中线性结构指的是数据元素之间存在着“一对一”的线性关系的数据结构。 

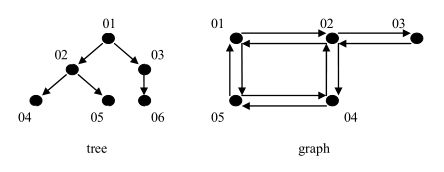
树状结构：除了一个数据元素（元素 01）以外每个数据元素有且仅有一个直接前驱元素，但是可以有多个直接后续元素。

特点是数据元素之间是 1 对 多的联系

       网络结构：每个数据元素可以有多个直接前驱元素，也可以有多个直接后续元素。特点是数据元素之间是多对 多 的联系

             问题：1个班的学生是什么逻辑结构呢？                      

数据的存储结构

数据的存储结构主要包括数据元素本身的存储以及数据元素之间关系表示，是数据的逻辑结构在计算机中的表示。

常见的存储结构有顺序存储，链式存储，索引存储，以及散列存储。

顺序存储结构：把逻辑上相邻的节点存储在物理位置上相邻的存储单元中，结点之间的逻辑关系由存储单元的邻接关系来体现。

由此得到的存储结构为顺序存储结构，通常顺序存储结构是借助于计算机程序设计语言（例如C/C++）的数组来描述的。 

（数据元素的存储对应于一块连续的存储空间，数据元素之间的前驱和后续关系通过数据元素，在存储器中的相对位置来反映）

     优点：

1.节省存储空间，因为分配给数据的存储单元全用存放结点的数据（不考虑c/c++语言中数组需指定大小的情况），结点之间的逻辑关系没有占用额外的存储空间。

2.采用这种方法时，可实现对结点的随机存取，即每一个结点对应一个序号，由该序号可以直接计算出来结点的存储地址。

缺点：

1.插入和删除操作需要移动元素，效率较低。

2.必须提前分配固定数量的空间，如果存储元素少，可能导致空闲浪费。

 

 

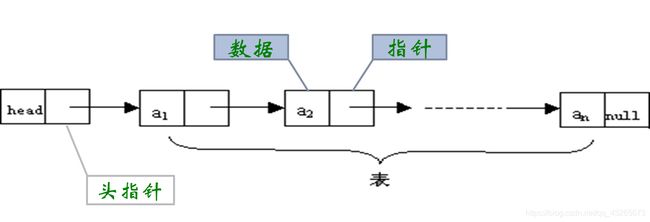
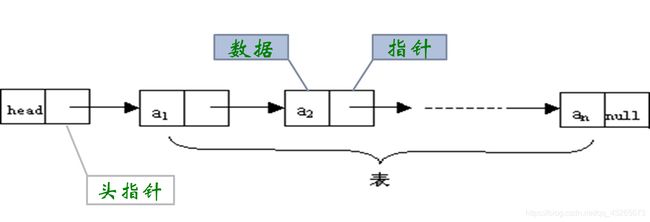
链式存储结构：数据元素的存储对应的是不连续的存储空间，每个存储节点对应一个需要存储的数据元素。

     每个结点是由数据域和指针域组成。 元素之间的逻辑关系通过存储节点之间的链接关系反映出来。

逻辑上相邻的节点物理上不必相邻。 

缺点：

1、比顺序存储结构的存储密度小 (每个节点都由数据域和指针域组成，所以相同空间内假设全存满的话顺序比链式存储更多)。 

2、查找结点时链式存储要比顺序存储慢。

优点：

1、插入、删除灵活 (不必移动节点，只要改变节点中的指针)。

2.有元素才会分配结点空间，不会有闲置的结点。

 

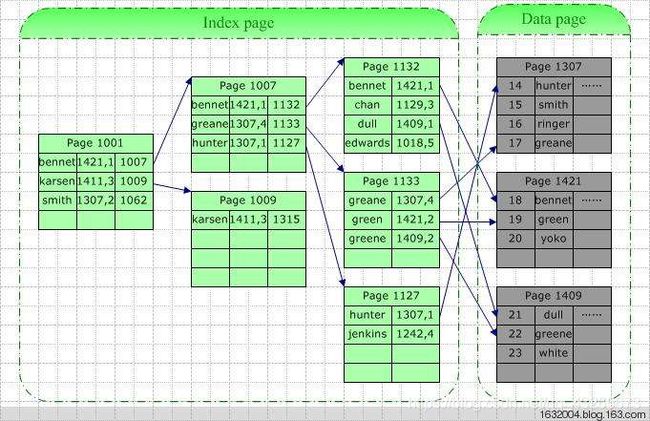
索引存储结构：除建立存储结点信息外，还建立附加的索引表来标识结点的地址。

     比如图书、字典的目录

 

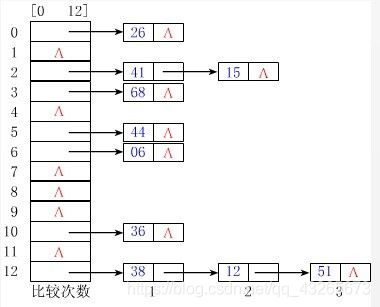
散列存储结构：根据结点的关键字直接计算出该结点的存储地址 HashSet HashMap

一种神奇的结构，添加、查询速度快。

 

举例：

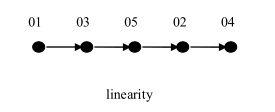
线性表的逻辑结构如图所示：

线性表逻辑结构对应的顺序存储结构为顺序表，对应的链式存储结构为链表。

     顺序表

链表

 

• 同一逻辑结构可以对应多种存储结构。
• 同样的运算，在不同的存储结构中，其实现过程是不同的

 

算法

算法（algorithm ）

是指令的集合，是为解决特定问题而规定的一系列操作。

它是明确定义的可计算过程，以一个数据集合作为输入，并产生一个数据集合作为输出。

一个算法通常来说具有以下五个特性：

1. 输入：一个算法应以待解决的问题的信息作为输入。
2. 输出：输入对应指令集处理后得到的信息。
3. 可行性：算法是可行的，即算法中的每一条指令都是可以实现的，均能在有限的时间内完成。
4. 有穷性：算法执行的指令个数是有限的，每个指令又是在有限时间内完成的，因此整个算法也是在有限时间内可以结束的。
5. 确定性：算法对于特定的合法输入，其对应的输出是唯一的。即当算法从一个特定输入开始，多次执行同一指令集结果总是相同的。

简单的说，算法就是计算机解题的过程。

在这个过程中，无论是形成解题思路还是编写程序，都是在实施某种算法。

前者是算法的逻辑形式，后者是算法的代码形式。

举例：如何求0+1+2+3+...10000=?

算法1：依次相加  while do-while  for

算法2：高斯解法：首尾相加*50    (1+10000)*10000/2    100*101/2

算法3：使用递归实现： sum(100) = sum(99)+100   sum(99)= sum(98)+99 .....   sum(2) = sum(1)+2   sum(1) = 1

 

评价算法优劣的依据：复杂度（时间复杂度和空间复杂度）

算法的复杂性体现在运行该算法时的计算机所需资源的多少上，计算机资源最重要的是时间和空间资源，因此复杂度分为时间和空间复杂度

时间复杂度是指执行算法所需要的计算工作量；

空间复杂度是指执行这个算法所需要的内存空间。

算法时间复杂度

时间复杂度（Time Complexity)）定义      

            时间频度：

              一个算法执行所耗费的时间，从理论上是不能算出来的，必须上机运行测试才能知道。

            但我们不可能也没有必要对每个算法都上机测试。

            一个算法花费的时间与算法中语句的执行次数成正比例，哪个算法中语句执行次数多，它花费时间就多。

            一个算法中的语句执行次数称为语句频度或时间频度，表示为T（n），n表示问题的规模

            时间复杂度

            但有时我们想知道它变化时呈现什么规律，想知道问题的规模，而不是具体的次数，此时引入时间复杂度。

            一般情况下，算法中基本操作重复执行的次数是问题规模n的某个函数，用T(n)表示，

            若有某个辅助函数f(n),使得当n趋近于无穷大时，T(n)/f(n)的极限值为不等于零的常数，则称f(n)是T(n)的同数量级函数。

            记作T(n)=O(f(n)),称O(f(n)) 为算法的渐进时间复杂度，简称时间复杂度。

           T(n)=O(f(n))

            或者说：时间复杂度就是时间频度去掉低阶项和首项常数。

            注意：时间频度与时间复杂度是不同的，时间频度不同但时间复杂度可能相同。              

            比如：某两个算法的时间频度是 T（n） = 100000n2+10n+6    T（n） = 10n2+10n+6   T(n) = n2   

            但是时间复杂度都是 T（n） = O（n2）                                         

            最坏时间复杂度和平均时间复杂度     

            最坏情况下的时间复杂度称最坏时间复杂度。一般不特别说明，讨论的时间复杂度均是最坏情况下的时间复杂度。

            这样做的原因是：最坏情况下的时间复杂度是算法在任何输入实例上运行时间的上界，这就保证了算法的运行时间不会比任何更长。

            在最坏情况下的时间复杂度为T(n)=O(n)，它表示对于任何输入实例,该算法的运行时间不可能大于O(n)。            

            平均时间复杂度是指所有可能的输入实例均以等概率出现的情况下，算法的期望运行时间。鉴于平均复杂度

            第一，难计算

            第二，有很多算法的平均情况和最差情况的复杂度是一样的。

            所以一般讨论最坏时间复杂度

            比如 我要求你在字典里查同一个字，告诉我这个字在字典的那一页。

            如果一页一页的翻，你需要多少时间呢？

            最优的情况就是这个字在第一页，

            最坏的情况就是这个字是 整本字典的最后一个字。

            所以即使我故意为难你，你也不会花费比找整本字典最后一个字还长的时间。

            当然，此时聪明的你就会想用部首、笔画等去查，才不要傻乎乎的一页一页翻，

            此时的你就会择优选择，因为此时你最坏得情况就是我给你部首笔画最多、除部首外笔画最多的一个超级复杂的一个字，但显然比翻整本字典快得多。

           

为了进一步说明算法的时间复杂度，我们定义 Ο、Ω、Θ符号。

Ο(欧米可荣)符号给出了算法时间复杂度的上界（最坏情况  <=），比如T（n） =O（n2）

Ω(欧米伽)符号给出了时间复杂度的下界（最好情况 >=），比如T（n） =Ω（n2）

而Θ(西塔)给出了算法时间复杂度的精确阶（最好和最坏是同一个阶  =），比如T（n） =Θ（n2）                      

时间复杂度计算

            根本没有必要计算时间频度，即使计算处理还要忽略常量、低次幂和最高次幂的系数，所以可以采用如下简单方法：

            ⑴ 找出算法中的基本语句；

　　                 算法中执行次数最多的那条语句就是基本语句，通常是最内层循环的循环体。

　　     ⑵ 计算基本语句的执行次数的数量级；

　　                 只需计算基本语句执行次数的数量级，这就意味着只要保证基本语句执行次数的函数中的最高次幂正确即可，

                        可以忽略所有低次幂和最高次幂的系数。这样能够简化算法分析，并且使注意力集中在最重要的一点上：增长率。

　　     ⑶ 用大Ο记号表示算法的时间性能。

　　                 将基本语句执行次数的数量级放入大Ο记号中。

时间复杂度举例          

• 一个简单语句的时间复杂度为O(1)。

int count=0;

• 100个简单语句的时间复杂度也为O(1)。（100是常数，不是趋向无穷大的n）

int count=0;

• 一个循环的时间复杂度为O(n)。

int n=8, count=0;

for (int i=1; i<=n; i++)

    count++;

T(n)=O(n)

• 时间复杂度为O(log2 n)的循环语句。

int n=8, count=0;

for (int i=1; i<=n; i*=2)

    count++;

1  2  4   8  16  32 

230=1024*1024*1024 = 1000*1000*1000=10亿

• 时间复杂度为O(n2)的二重循环。

int n=8, count=0;

for (int i=1; i<=100n; i++)

    for (int j=1; j<=10n; j++)

        count++;

• 时间复杂度为O(nlog2n)的二重循环。

int n=8, count=0;

for (int i=1; i<=n; i*=2)

    for (int j=1; j<=n; j++)

        count++;           

• 时间复杂度为O(n2)的二重循环。

int n=8, count=0;

for (int i=1; i<=n; i++)

    for (int j=1; j<=i; j++)

        count++;

1+2+3+4....+n=(1+n)*n/2

需要复杂些数学运算：1+2+3+.....+n=(n+1)*n/2  时间复杂度是 O(n2)

 查找和排序算法会大量的设计时间复杂度，作为选择查找和排序算法的重要依据

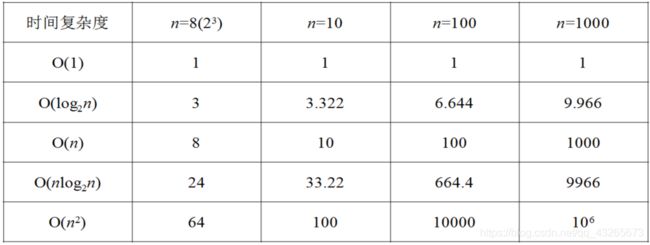
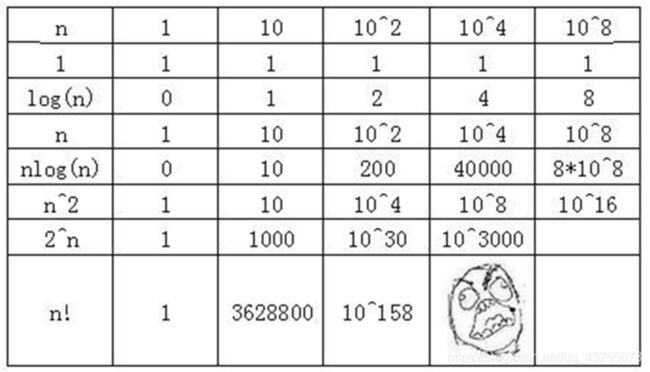
常用的时间复杂度级别

            常数阶O(1)

            对数阶O(log2n)

            线性阶O(n)

            线性对数阶O(n*log2n)

            平方阶O(n2)

            立方阶O(n3)

            ...

            k次方阶O(nk)

            指数阶O(2n)

            阶乘阶O(n!)           

            上面各种时间复杂度级别，执行效率越来越低。

 生活案例：排队打饭，排队进地铁站，上地铁

技术案例：多线程中就绪队列和阻塞队列

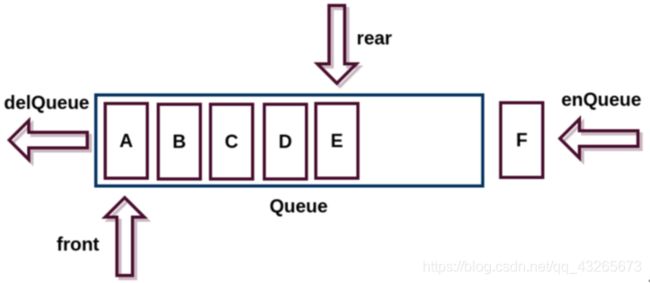
对于队列的主要操作是入队和出队操作

public interface Queue {

// 返回队列的大小

public int getSize();

// 判断队列是否为空

public boolean isEmpty();

// 数据元素 e 入队

public void enqueue(Object e);

// 队首元素出队

public Object dequeue();

// 取队首元素

public Object peek();

}      

队列的存储结构

            顺序队列

            方法1：使用数组作为存储结构：

 缺点：通过出队操作将数据弹出队列后，front之前的空间还能够再次得到吗？

                不能。所以使用普通数组实现队列，就再也不能使用front之前的空间了，这会导致大量空间丢失

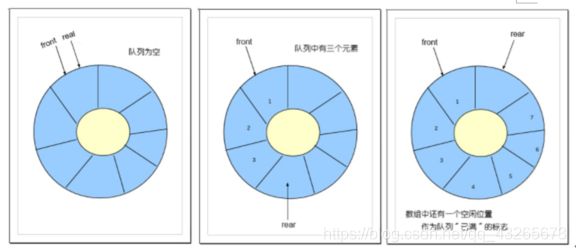
            方法2：使用循环数组作为存储结构：           

            为了解决这个问题，将普通数组换成循环数组。在循环数组中，末尾元素的下一个元素不是数组外，而是数组的头元素。

            这样就能够再次使用front之前的存储空间了

     链式队列

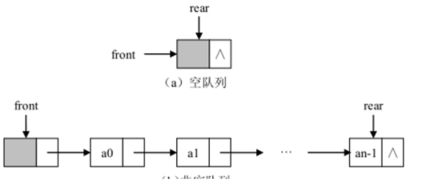
            队列的链式存储可以使用单链表来实现。

            为了操作实现方便，这里采用带头结点的单链表结构。

            根据单链表的特点，选择链表的头部作为队首，链表的尾部作为队尾。

            除了链表头结点需要通过一个引用来指向之外，还需要一个对链表尾结点的引用，以方便队列的入队操作的实现。

            为此一共设置两个指针，一个队首指针和一个队尾指针，如图 所示。

            队首指针指向队首元素的前一个结点，即始终指向链表空的头结点，队尾指针指向队列当前队尾元素所在的结点。

            当队列为空时，队首指针与队尾指针均指向空的头结点

双端队列deque  double ended queue  通常读为“deck”

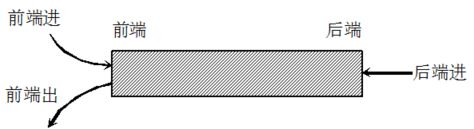
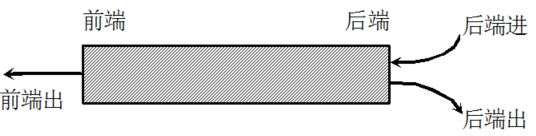
所谓双端队列是指两端都可以进行进队和出队操作的队列，如下图所示，将队列的两端分别称为前端和后端，两端都可以入队和出队。其元素的逻辑结构仍是线性结构

 

在双端队列进队时：前端进的元素排列在队列中后端进的元素的前面，后端进的元素排列在队列中前端进的元素的后面。在双端队列出队时，无论前端出还是后端出，先出的元素排列在后出的元素的前面。

输出受限的双端队列，即一个端点允许插入和删除，另一个端点只允许插入的双端队列。

 输入受限的双端队列，即一个端点允许插入和删除，另一个端点只允许删除的双端队列。

      双端队列既可以用来队列操作，也可以用来实现栈操作（只操作一端就是栈了）

Java中的栈和队列类

Stack类：栈类  过时    public class Stack extends Vector

Queue：队列类

Deque：双端队列（栈操作建议使用）

public class LinkedList

    extends AbstractSequentialList

    implements List, Deque, Cloneable, java.io.Serializable

public interface Deque extends Queue   扩展了java.util.Collection接口

双端队列

public interface Queue extends Collection 

扩展了java.util.Collection接口

Queue使用时要尽量避免Collection的add()和remove()方法，而是要使用offer()来加入元素，使用poll()来获取并移出元素。它们的优点是通过返回值可以判断成功与否，add()和remove()方法在失败的时候会抛出异常。 如果要使用前端而不移出该元素，使用element()或者peek()方法。

所以Java中实现栈和队列操作都可以通过使用LinkedList类实现，当然底层使用的链表。

public class ArrayDeque extends AbstractCollection

                           implements Deque, Cloneable, Serializable

ArrayDeque是Deque 接口的大小可变数组的实现

/**

 * 功能：模拟生活中罗盘子案例

 * 技能：LinkedList

 *

 * LinkedList既可以当做线性表处理，也可以当做栈、队列使用

 * @author Administrator*

 */

public class TestDeque {

public static void main(String[] args) {

    //创建一个栈

    Deque deque =  new LinkedList();     

    //罗盘子:入栈

//     deque.addFirst("盘子1");

//     deque.addFirst("盘子2");

//     deque.addFirst("盘子3");

    deque.push("盘子1");

    deque.push("盘子2");

    deque.push("盘子3");    

    //获取最上面的盘子：获取栈顶元素

//     System.out.println(deque.getFirst());

//     System.out.println(deque.getFirst());

//     System.out.println(deque.getFirst());

    System.out.println(deque.peek());

    System.out.println(deque.peek());

    System.out.println(deque.peek());    

    //拿走盘子：出栈

//     System.out.println(deque.removeFirst());

//     System.out.println(deque.removeFirst());

//     System.out.println(deque.removeFirst());

    System.out.println(deque.pop());

    System.out.println(deque.pop());

    System.out.println(deque.pop());

}

}

/**

 * 功能：模拟生活中超市购物排队结算

 * 技能：使用LinkedList实现队列的操作

 *

 * @author Administrator

 *

 */

public class TestQueue {

public static void main(String[] args) {

    //创建一个队列

    java.util.Queue queue = new LinkedList();   

    //入队

    queue.offer("张三");

    queue.offer("李四");

    queue.offer("王五");

    //获取队头元素

    System.out.println(queue.element());

    System.out.println(queue.element());

    System.out.println(queue.element());

    //出队

    System.out.println(queue.remove());

    System.out.println(queue.poll());

    queue.offer("赵六");

    System.out.println(queue.poll());

    System.out.println(queue.poll());

    System.out.println(queue.poll());

    System.out.println(queue.poll());

    System.out.println(queue.poll());

}

}

/**

 * 借助栈实现进制转换（10----2）

 * @author Administrator

 *

 */

public class TestConversion {

public static void main(String[] args) {    

    int n = 13;

    int t = n;

    //String str = "";

    Deque  deque = new LinkedList();

    while(t>0){

       //除以2得到余数作为二进制位

       int mod = t%2;

       //System.out.print(mod);

       //str = mod + str;

       deque.push(mod);

       //除以2得到商作为被除数继续

       int result = t/2;

       t = result;

    }

    System.out.print(n+"--------->");

    while(!deque.isEmpty()){

       System.out.print(deque.pop());

    }     

}

}