二叉搜素树（BSTree）详解—— C++ 数据结构

传统艺能

小编是双非本科大一菜鸟不赘述，欢迎大佬指点江山，QQ - 1319365055

非科班转码社区诚邀您入驻
小伙伴们，打码路上一路向北，彼岸之前皆是疾苦
一个人的单打独斗不如一群人的砥砺前行
诚邀各位有志之士加入！！
直达： 社区链接点我

---

BSTree

二叉搜索树，binary search tree，因此也叫他 BS 树。

二叉搜索树排列规则是小于根节点的全部在左子树，大于根节点的全部在右子树，正因为如此他在二叉树基础上获得了可以搜索的属性，如下：

每个节点都满足如上特点那他就是一个二叉搜索树。

初始化

二叉搜索树的初始化其实和二叉树大同小异：

template<class K>
struct BSTreeNode
{
	BSTreeNode<K>* _left;//左子树
	BSTreeNode<K>* _right;//右子树
	K _key;//值

	BSTreeNode(const K& key)
		:_left(nullptr)
		, _right(nullptr)
		, _key(key)
	{}
};

在实现具体功能之前的大框架：

template<class T>
class BSTree
{
   typedef BSTreeNode<T> node;//typedef 方便使用
 public:
      //需要实现的功能函数
 private:
    node* _root = nullptr;
};

中序遍历

中序遍历搜索二叉树结构能够打印出顺序排列的元素，为了方便观察我们遍历都使用中序遍历：

void _InOrder(Node* root)
	{
		if (root == nullptr)
			return;


		_InOrder(root->_left);
		cout << root->_key << " ";
		_InOrder(root->_right);
	}


	void InOrder()
	{
		_InOrder(_root);
		cout << endl;
	}

insert 插入

这里插入函数 insert 实际需要考虑三种具体情况：

1. 根节点为空，左右子树无法访问
2. 插入值比根节点小，左子树插入；比根节点大，右子树插入

第一种情况：

     bool Insert(const K& key)
	{
		if (_root == nullptr)
		{
			_root = new Node(key);
			return true;
		}

第二种情况：

注意！正常情况时，我们在最后找到的位置进行插入，但别忘了这是一个二叉树结构，插入时需要维持前后节点的衔接，因此既要达到插入新节点还要维持结构关系，我们就需要一个parent 双亲节点来进行传递：

		Node* parent = nullptr;
		Node* cur = _root;
		while (cur)
		{
		    //寻找插入位置
			if (cur->_key < key)
			{
				parent = cur;
				cur = cur->_right;
			}
			else if (cur->_key > key)
			{
				parent = cur;
				cur = cur->_left;
			}
			else
			{
				return false;
			}
		}
		//通过双亲节点关系进行插入
		cur = new Node(key);
		if (parent->_key < cur->_key)
		{
			parent->_right = cur;
		}
		else
		{
			parent->_left = cur;
		}


		return true;
	}

递归版本

递归实现上虽然没有像非递归那样容易理解，但是代码和思路上个人觉得是更为简单和巧妙：
仅仅利用二叉树的遍历，分别在左子树和右子树进行递归，搜索到需要插入的节点位置，而且更妙的是这个方法不需要借助 parent 双亲节点的帮助，因为递归会自动返回上一层的缘故，无形中构建了节点的前后联系，因此直接一步到位即可，是不是有种爽文手段的感觉。

	bool _InsertR(Node*& root, const K& key)
	{
		if (root == nullptr)
			root = new Node(key);


		if (root->_key < key)
			return _InsertR(root->_right, key);//递归左子树
		else if (root->_key > key)
			return _InsertR(root->_left, key);//递归右子树
		else
			return false;
	}
//写成接口方便修改和调用
	bool InsertR(const K& key)
	{
		return _InsertR(_root, key);
	}

find 查找

其实查找就是小儿科，因为在 insert 插入函数中已经实现了，思路还是左右子树的分治，代码也很容易理解不赘述：

	Node* Find(const K& key)
	{
		Node* cur = _root;
		while (cur)
		{
			if (cur->_key < key)
				cur = cur->_right;
			else if (cur->_key > key)
				cur = cur->_left;
			else
				return cur;
		}
		return NULL;
	}

递归版本

其实 find 的递归版本没什么优化可言，查找使用递归反而在递归深度很大会拉垮效率，谨慎使用个人还是更推荐非递归版本：

	Node* _FindR(Node* root, const K& key)
	{
		if (root == nullptr)
			return nullptr;


		if (root->_key < key)
			return _FindR(root->_right, key);
		else if (root->_key > key)
			return _FindR(root->_left, key);
		else
			return  root;
	}

erase 删除

删除节点算是二叉搜索树里面最难的一个接口实现了，整体思路上会比较繁琐，我们还是先以非递归的方法入手：
分为三种情况，该节点左为空，右为空，左右都不为空，最后一种情况要复杂一点。

	bool Erase(const K& key)
	{
		Node* parent = nullptr;
		Node* cur = _root;
		while (cur)
		{
			if (cur->_key < key)
			{
				parent = cur;
				cur = cur->_right;
			}
			else if (cur->_key > key)
			{
				parent = cur;
				cur = cur->_left;
			}
			else//找到了 key 值对应节点
			{
				// 1.左为空
				if (cur->_left == nullptr)
				{
					if (parent == nullptr)
					{
						_root = cur->_right;//双亲节点为空，根节点转移到右子树
					}
					else
					{
						if (cur == parent->_left)
							parent->_left = cur->_right;
						else
							parent->_right = cur->_right;
					}
					delete cur;
				}
				//2.右为空
				else if (cur->_right == nullptr)
				{
					if (parent == nullptr)
					{
						_root = cur->_left;
					}
					else
					{
						if (cur == parent->_left)
							parent->_left = cur->_left;
						else
							parent->_right = cur->_left;
					}
					delete cur;
				}
				// 3.左右都不为空
				else
				{
				//实现
				}

左右都不为空时，因为面对左子树和右子树都要重新构建与上层联系，且还要维持搜索树原有的结构，因此我们使用替换法删除

需要先找到左树的最大节点(最右节点) 或者是右树的最小节点(最左节点)，这个节点就是删除后用来做新的根节点的最佳人选，这里以右子树为例：

					Node* minNodeParent = cur;  // 这里要注意不能初始化给空
					Node* minNode = cur->_right;
					while (minNode->_left)
					{
						minNodeParent = minNode;
						minNode = minNode->_left;
					}
					swap(cur->_key, minNode->_key);
					
					// 转换成删除minNode，因为minNode是作为空的节点，可以直接删除
					
					if (minNodeParent->_right == minNode)
						minNodeParent->_right = minNode->_right;
					else
					minNodeParent->_left = minNode->_right;
					delete minNode;
				}
				return true;
			}
		}
		return false;

检验

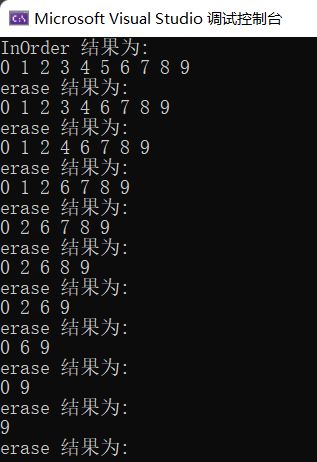
以 test 代码检验一下当前执行情况

void TestBSTree()
{
	int a[] = { 5, 3, 4, 1, 7, 8, 2, 6, 0, 9 };
	BSTree<int> bst;
	for (auto e : a)
	{
		//bst.Insert(e);
		bst.Insert(e);	
	}
	cout << "InOrder 结果为:" << endl;
	bst.InOrder();
	for (auto e : a)
	{
		bst.Erase(e);
		cout << "erase 结果为:" << endl;
		bst.InOrder();
	}
}

是没有问题滴，所以今天就到这里吧，aqa 芭蕾 eqe 亏内，代表着开心代表着快乐，ok 了家人们。