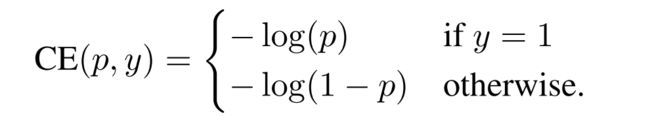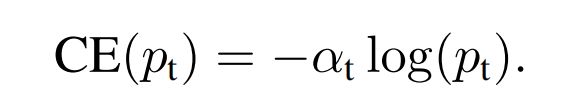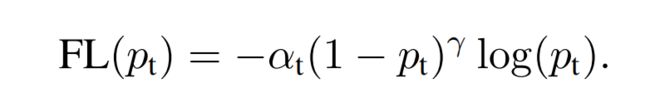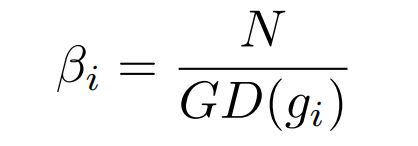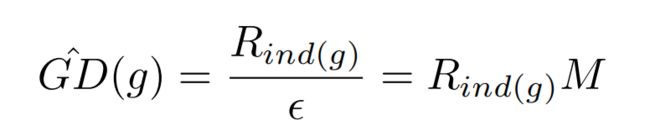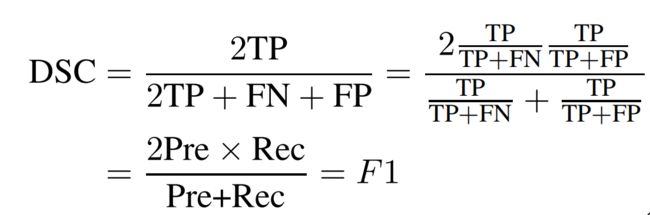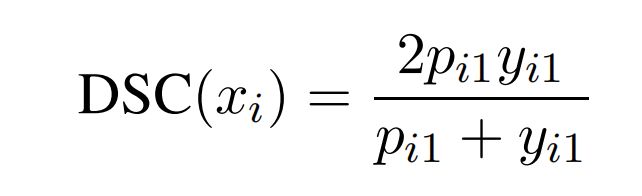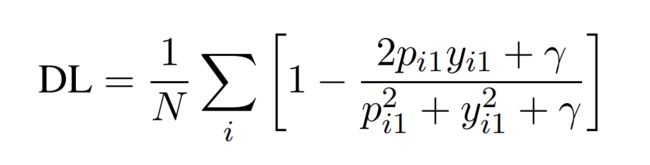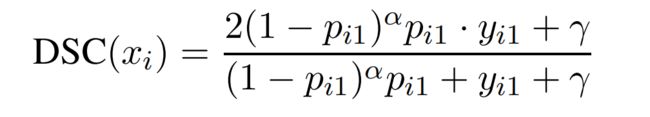分类模型-类别不均衡问题之loss设计
这个系列将记录下本人平时在深度学习方面觉得实用的一些trick,可能会包括性能提升和工程优化等方面。
该系列的代码会更新到Github
炼丹系列1: 分层学习率&梯度累积
炼丹系列2: Stochastic Weight Averaging (SWA) & Exponential Moving Average(EMA)
前言
数据类别不均衡是很多场景任务下会遇到的一种问题。比如NLP中的命名实体识别NER,文本中许多都是某一种或者几种类型的实体,比如无需识别的不重要实体;又或者常见的分类任务,大部分数据的标签都是某几类。
而我们又无法直接排除这些很少的类别的数据,因为这些类别也很重要,仍然需要模型去预测这些类别。
数据采样
有时会从数据层面缓解这种类别不均衡带来的影响,主要是过采样和欠采样。
- 过采样:对于某些类别数据比较少,对它们进行重复采样,以达到相对平衡,重复采样的时候,有时也会对数据加上一点噪声;
- 欠采样:对于某些类别数据特别多,只使用部分数据,抛弃一些数据;
过采样可能导致这些类别产生过拟合的现象,而欠采样则容易导致模型的泛化性变差。
另外,比较常用的则是结合ensemble方法,则将数据切分为N部分,每部分都包含数据少的类别的所有样本和数据多的类别的部分样本,训练N个模型,最后进行集成。
缺点是,使用ensemble则会提高部署成本和带来性能问题。
损失函数
如果在损失函数方面下功夫,针对这种类别不均衡的场景设计一种loss,能够兼顾数据少的类别,这其实是一种更理想的做法,因为不会破坏原数据的分布,并且不会带来性能问题(对训练速度可能有轻微的影响,但不影响推理速度)。
下面,我们就介绍在这方面几种常用的loss设计。
Focal Loss
Focal Loss是一种专门为类别不均衡设计的loss,在《Focal Loss for Dense Object Detection》这篇论文中被提出来,应用到了目标检测任务的训练中,但其实这是一种无关特定领域的思想,可以应用到任何类别不均衡的数据中。
首先,还是从二分类的cross entropy (CE) loss入手:
为了符号的方便, C E ( p , y ) = C E ( p t ) = − l o g ( p t ) CE(p,y)=CE(p_t)=-log(p_t) CE(p,y)=CE(pt)=−log(pt)
p ∈ [ 0 , 1 ] p\in [0,1] p∈[0,1]为模型对于label=1(ground-truth)的类别的预测概率。
问题分析
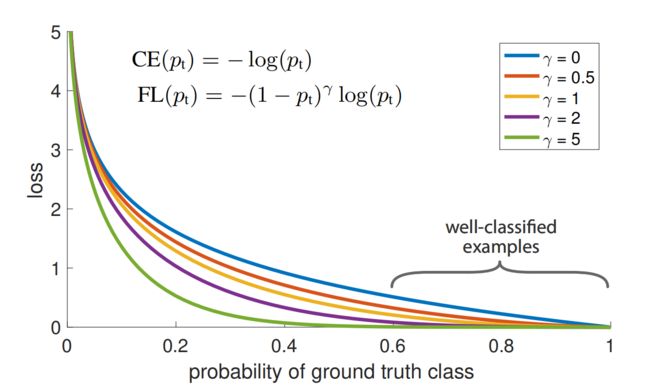
下图的蓝色曲线为原生的CE loss,容易看出来,那些容易分类( p t ≫ 0.5 p_t \gg 0.5 pt≫0.5)的样本也会产生不小的loss,但这些大量的容易样本的loss加起来,会压过那些稀少类别的样本的loss。
CE改进
针对类别不均衡,普遍的做法是 α \alpha α-balanced CE。给CE loss增加一个权重因子 α \alpha α,正样本权重因子为 α ∈ [ 0 , 1 ] \alpha \in [0,1] α∈[0,1],负样本为 1 − α 1-\alpha 1−α
实际使用中,一般设置为类别的逆反频率,即频率低的类别权重应该更大,比如稀少的正样本的 α \alpha α为负样本的频率。或者当作一个超参数。
但是,这种做法只是平衡了正负样本的重要性,无法区分容易(easy)样本和困难(hard)样本,这也是类别不均衡的数据集很容易出现的问题:容易分类的样本贡献了大部分的loss,并且主导了梯度。
因此,Focal Loss的主要思想就是让loss关注那些困难样本,而降低容易样本的重要性。
如上式,在CE的基础增加一个调节因子 ( 1 − p t ) γ , w h e r e γ ≥ 0 (1-p_t)^{\gamma},where\ \gamma\ge0 (1−pt)γ,where γ≥0。上图1可以看出, γ \gamma γ越大,容易样本的loss贡献越小。
Focal Loss具有以下两个属性:
- 当一个样本被错误分类时,且 p t p_t pt很小时(即为困难样本),那么调节因子是接近1的,loss则基本不受影响。而相反的,当 p t → 1 p_t \to 1 pt→1,分类很好的样本(容易样本),调节因子则会偏于0,loss贡献变得很小;
- 不同的 γ \gamma γ参数可以平滑地调整容易样本的重要性降低的比率。当 γ = 0 \gamma=0 γ=0时,则等同于普通的CE。而当 γ \gamma γ变大时,那么调节因子的影响也会同样变大,即容易样本的重要性会降低。
论文在实验中,Focal Loss还保留上述的权重因子 α t \alpha_t αt:
通常来说,当增加 γ \gamma γ时, α \alpha α应该稍微降低。
在作者的实验中, γ = 2 , α = 0.25 \gamma=2,\alpha=0.25 γ=2,α=0.25取得了最佳性能。
这里的 α \alpha α是稀少类别的权重因子,但按照上述 α \alpha α-balanced CE的分析,稀少类别的权重因子应该更大才对。但 γ \gamma γ和 α \alpha α是互相作用的,论文经过多次实验,调整 γ \gamma γ带来的收益更大,而大的 γ = 2 \gamma=2 γ=2,应该搭配小的权重因子 α = 0.25 \alpha=0.25 α=0.25.
GHM(Gradient Harmonizing Mechanism)
梯度调和机制Gradient Harmonizing Mechanism的设计目的也是为了解决不均衡类别的问题而对loss函数进行优化,出自《Gradient Harmonized Single-stage Detector》。
介绍
GHM同样表述了关于容易样本和困难样本的观点A:模型从容易分类的样本的到收益很少,模型应该关注那些困难分类的样本,不管它属于哪一种类别,但大量的容易样本加起来的贡献会盖过困难样本,使得训练效益很低;
进一步指出Focal Loss的问题,提出不同的观点B:
- Focal Loss存在两个超参数,并且是互相影响,构成许多参数组合,会导致调参需要很多尝试成本;并且,Focal Loss是一种静态的loss,那么同一种超参数无法适用于不同的数据分布;
- 有一些特别困难分类的样本,它们很可能是离群点,加入这些样本的训练,会影响模型的稳定性;
- 提出了**gradient density(梯度密度)**的梯度调和机制,来缓解这种类别不均衡的问题。
下图左展示了上述观点A,梯度范数gradient norm的大小则代表样本的分类难易程度,收益实际即对应为梯度;
下图中和右展示了通过GHM的梯度调和之后,容易样本的gradient norm会被削弱许多,并且特别困难的样本也会被轻微削弱,分别对应观点A和观点B-2的解决方案。
理论
基于这些分析,论文提出了一种梯度调和机制GHM(Gradient Harmonizing Mechanism),其主要思想是:首先仍然是降权大量容易样本贡献的梯度总和,其次是对于那些特别困难样本即离群点,也应当相对地降权。
对于二分类问题,同样的交叉熵loss如下:
其中, p ∈ [ 0 , 1 ] p\in[0,1] p∈[0,1]为模型的预测概率, p ∗ ∈ { 0 , 1 } p^* \in \{0,1\} p∗∈{0,1}为真实的标签 ground-truth label;
x为模型unnormalized的直接输出, p = s i g m o i d ( x ) p=sigmoid(x) p=sigmoid(x)
这里的g为gradient norm,可以用来表示一个样本的分类难易程度以及对在全局梯度中的影响程度,g越大则分类难度越高。
下图2展示了在目标检测模型中gradient norm的分布情况,表明了容易样本在梯度中会占主导地位,以及模型无法处理一些特别困难的样本,这些样本的数量甚至超过了中等困难的样本,但模型不应过于关注这些样本,因为它们可以认为是离群点。(对应上述观点A和观点B-2)
为了解决这种gradient norm的分布问题,论文提出了一种调和手段:Gradient Density
其中, g k g_k gk为第k个样本的gradient norm。
g的梯度密度即 G D ( g ) GD(g) GD(g)表示落于以g为中心,长度为 ϵ \epsilon ϵ的中心区域的样本数量,然后除以有效长度进行标准化。
那么,梯度密度调和参数为:
N为样本数量。
G D ( g i ) / N GD(g_i)/N GD(gi)/N 可以看作是梯度上在第i个样本周边样本频率的一种正则化:
- 如果所有样本的梯度是均匀分布的,那么对于每个样本i: G D ( g i ) = N → β i = 1 GD(g_i)=N \to \beta_i=1 GD(gi)=N→βi=1,意味着每个样本都没起到任何改变;
- 见上图2,容易样本的频率很高,那么 β \beta β就会变得很小,起到降低这些样本的权重的效果;并且特别困难样本即离群点的频率会比中等困难的样本频率多,意味着这些离群点的 β \beta β会相对较小,那么也会相对地轻微降低这些样本的权重;
- 从第2点可以看出,GHM其实只适用于那些容易样本和特别困难样本的数量比中等困难样本多的场景。
因此,经过GHM调和之后的loss为:
计算优化
很容易算出,GHM的计算复杂度是 O ( N 2 ) O(N^2) O(N2),论文通过Unit Region的方法来逼近原生的梯度密度,大大降低了计算复杂度。
首先,将gradient norm的值域空间[0,1]划分为M个长度为 ϵ \epsilon ϵ的Unit Region。对于第j个Unit Region: r j = [ ( j − 1 ) ϵ , j ϵ ) r_j=[(j-1)\epsilon,j\epsilon) rj=[(j−1)ϵ,jϵ)
接着,让 R j R_j Rj等于落在 r j r_j rj的样本数量;并且,定义 i n d ( g ) = t , s . t . ( t − 1 ) ϵ < g < t ϵ ind(g)=t,s.t. (t-1)\epsilon
则,梯度密度的近似函数如下,得到计算复杂度优化的GHM Loss:
这里怎么理解这种近似思想呢:
- 先回忆原生GHM的梯度密度计算:g的梯度密度即 G D ( g ) GD(g) GD(g)表示落于以g为中心,长度为 ϵ \epsilon ϵ的中心区域的样本数量,然后除以有效长度进行标准化;
- 将gradient norm划分了M个Unit Region之后,假如第i个样本的 g i g_i gi落入第j个Unit Region,那么同样落入该Unit Region的样本可以认为是落于以 g i g_i gi为中心的中心区域,并且有效长度为 ϵ \epsilon ϵ,即得到上述的近似梯度密度函数。
结合EMA
最后,在使用Unit Region优化之后,还结合 Exponential moving average(EMA)的思想,让梯度密度更加平滑,减少对极端数据的敏感度:
R i ( t ) R_i^{(t)} Ri(t)为在t次遍历中,落入第j个Unit Region的数量;
α \alpha α即为EMA中的momentum参数。
超参数实验
Dice Loss
Dice Loss来自《Dice Loss for Data-imbalanced NLP Tasks》这篇论文,阐述在NLP的场景中,这种类别数据不均衡的问题也是十分常见,比如机器阅读理解machine reading comprehension (MRC),与上述论文表明的观点大致相同:
- 负样本数量远超过正样本,导致容易的负样本会主导了模型的训练;
- 另外,还指出交叉熵其实是准确率(accuracy)导向的,导致了训练和测试的不一致。在训练过程中,每一个样本对目标函数的贡献是相同,但是在测试的时候,像分类任务很重要的指标F1 score,由于正样本数量很少,每一个正样本就对于F1 score的贡献则更多了。
Dice Coeffificient
dice coeffificient是一种F1导向的统计,用于计算两个集合的相似度:
对应到二分类场景中,A是模型预测为正样本的样本集合,B是真实的正样本集合。此时,dice coefficient其实等同于F1:
对于每一个样本 x i x_i xi,它对应dice coefficient的为:
但是,显而易见,这样会导致负样本( y i 1 = 0 y_{i1}=0 yi1=0)对目标的贡献为0。因此,为了避免负样本的作用为0,让训练更加平滑,在分子和分母中同时加入一个因子 γ \gamma γ:
为了更快地收敛,分母可以为平方的形式,那么Dice Loss(DL)则变为:
(修改为1-DSC,目的是让DSC最大化变成目标函数最小化,这是loss函数常用的转换套路了,并且让loss为正数)
另外,以计算set-level的dice coefficient,而不是独立样本的dice coefficient加起来,这样可以让模型更加容易学习:
自调节
上述未经过平滑的DSC公式其实是F1的soft版本,因为对于F1 score,只存在正判或误判。模型预估通常以0.5为边界来判断是否为正样本:
DSC使用连续的概率p,而不是使用二分 I ( p i 1 > 0.5 ) \mathbb{I}(p_{i1}>0.5) I(pi1>0.5),这种gap对于均衡的数据集不是什么大问题。
但是对于大部分为容易的负样本的数据集来说,是存在极端的害处:
- 容易分类的负样本很容易主导整个训练过程,因为它们的预测概率相对来说更容易接近0;
- 同时,模型会变得难以区分困难分类的负样本和正样本,这对于F1 score的表现有着很大的负向影响。
为了解决这种问题,DSC在原来的基础上,给soft概率p乘上一个衰减因子 ( 1 − p ) (1-p) (1−p):
( 1 − p i 1 ) α (1-p_{i1})^{\alpha} (1−pi1)α是一个与每一个样本关联的权重,并且在训练过程会动态改变,根据样本的分类难易程度,实现对样本权重的自调节:
( 1 − p i 1 ) α p i 1 (1-p_{i1})^{\alpha}p_{i1} (1−pi1)αpi1对于预测概率接近0和1的容易样本,该值明显小很多,可以减少模型对这些样本的关注。
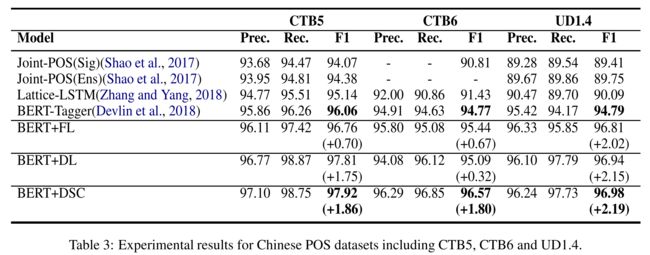
实验结果
Label Smoothing
最后再讲一下标签平滑,它不是针对不均衡类别设计的loss优化,但不失为一种提升分类模型泛化能力的有效措施。
出自这篇论文《Rethinking the Inception Architecture for Computer Vision》,它是交叉熵loss的另外一种正则化形式:Label Smoothing。
cross-entropy
在K分类模型中,第k个label的预估概率为:
p ( k ∣ x ) = e x p ( z k ) ∑ i = 1 K e x p ( z i ) p(k|x)=\frac{exp(z_k)}{\sum^K_{i=1}exp(z_i)} p(k∣x)=∑i=1Kexp(zi)exp(zk)
k ∈ 1 , 2 , . . . . , K k\in {1,2,....,K} k∈1,2,....,K, z i z_i zi为logits
ground-truth真实label为: q ( k ∣ x ) , ∑ k q ( k ∣ x ) = 1 q(k|x),\ \sum_kq(k|x)=1 q(k∣x), ∑kq(k∣x)=1
那么,对应的交叉熵loss则为:
ℓ = − ∑ k = 1 K l o g ( p ( k ) ) q ( k ) \ell =-\sum^K_{k=1}log(p(k))q(k) ℓ=−∑k=1Klog(p(k))q(k)
存在问题
对 z k z_k zk求导得到梯度为: ∂ ℓ ∂ z k = p ( k ) − q ( k ) \frac{\partial \ell}{\partial z_k}=p(k)-q(k) ∂zk∂ℓ=p(k)−q(k),并且范围在-1到1
对于我们的交叉熵loss,最小化则等同于真实标签的最大似然,而仅当 q ( k ) = δ k , y q(k)=\delta_{k,y} q(k)=δk,y时才能达到最大似然, δ k , y \delta_{k,y} δk,y当k=y时为1,其他则为0。
而对于有限值的 z k z_k zk是无法达到这种最大似然的情况,但可以接近这种情况,当所有的 z y ≫ z k f o r k ≠ y z_y \gg z_k\ for\ k\neq y zy≫zk for k=y,即当对应ground-truth的logits远远大于其他的logits,直观上来看,这是由于模型对自己的预测结果太过于自信了,这会产生以下两个问题,:
- 它可能会造成过拟合。如果模型学习到了为每个样本的ground-truth label赋予完全的概率,那这无法保证泛化性;
- 它鼓励最大的logit和其他的logits差别尽可能大,再加上梯度的边界仅在-1到1,这会降低模型的适应(adapt)能力。
正则化
基于上述分析,作者提出了一种优化的交叉熵,增加了正则化:label-smoothing regularization
其中, ϵ \epsilon ϵ为[0, 1]的超参数,K为标签类别数量。
- 这种方法避免了最大的logit比其他logits太过于大,给模型增加了正则化,提升了模型的泛化能力;
- 即使发生这种情况,交叉熵loss会变得更大,因为不同于 q ( k ) = δ k , y q(k)=\delta_{k,y} q(k)=δk,y,每个 q ′ ( k ) q^{'}(k) q′(k)都会贡献loss。
在论文中,ImageNet数据集的实验中, ϵ \epsilon ϵ取值为0.1。
总结
- 本文介绍了几种针对类别不均衡的数据集提出的解决思路,主要的观点都是数量很多的类别存在许多容易分类的样本,这些对于模型训练的贡献很小,但由于数据巨大,会主导模型的训练过程;
- Focal Loss和Dice Loss思想比较接近,都是为了减少模型对容易样本的关注而进行的loss优化,而GHM Loss除了对容易样本降权,还实现了对特别困难样本的轻微降权,因为特别困难的样本可以认为是离群点;
- GHM Loss仅适用于二分类,而Focal Loss和Dice Loss很容易扩展到多分类,但实际使用中Focal Loss对于多分类调参比较困难(每种类别对应的 α \alpha α-balanced,加上 γ \gamma γ,参数组合过于多);
- 最后介绍的Label Smoothing虽然不是针对类别不均衡的问题,但在分类模型中,其效果往往比原生的交叉熵有些小提升。
代码实现
tensorflow及torch的实现:github