炼丹系列2: Stochastic Weight Averaging (SWA) & Exponential Moving Average(EMA)

这个系列将记录下本人平时在深度学习方面觉得实用的一些trick，可能会包括性能提升和工程优化等方面。
该系列的代码会更新到Github
炼丹系列1: 分层学习率&梯度累积
炼丹系列2: Stochastic Weight Averaging (SWA) & Exponential Moving Average(EMA)

Exponential Moving Average(EMA)

介绍

EMA（Exponential Moving Average）全称为指数移动平均，主要作用是平滑模型权重，平滑可以带来更好的泛化能力。

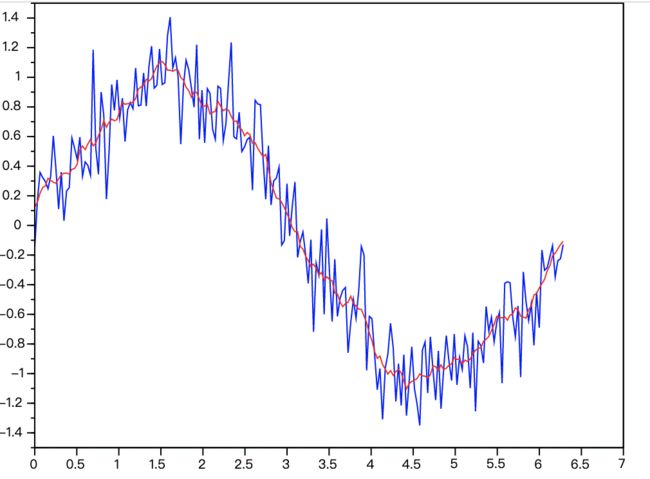
以下是来自wiki关于移动平均（Moving Average）的图片，对带有噪声的正弦函数使用Moving Average进行平滑后的效果。

蓝色为带噪声的正弦曲线，红色为平滑曲线。

首先，来看下它的公式：

$w_{shado{w}_t}=\alpha \ast w_{shado{w}_{t-1}}+(1-\alpha )\ast w_t$

• 其中，$w_{shadow}$是EMA权重，一般也称为shadow（影子）权重；
• $\alpha$是衰退率，一般取接近1的数，如0.999或者0.9999；
• $w$即为模型的权重。

从上述公式来看，shadow权重的更新大部分由累积的权重决定，小部分由当前权重决定。并且shadow权重不会参与模型权重的更新，最终使用shadow权重来作为模型的权重。

EMA的思想大体为：shadow权重是通过历史的模型权重指数加权平均数来累积的，每次shadow权重的更新都会受上一次shadow权重的影响，所以shadow权重的更新都会带有前几次模型权重的惯性，历史权重越久远，其重要性就越小，这样可以使得权重更新更加平滑。

其实，这个公式在Momentum、Adma优化器中都可以见到它的身影，我们就按照Momentum优化器的思想类比来理解它。

$\{\begin{array}{l}{v}_t=\beta v_{t-1}+(1-\beta )dw\\ w_t=w_{t-1}-\alpha v_t\end{array}$

同理，每次梯度的更新会受前几次梯度方向的惯性影响。当梯度方向保持不变时，加上惯性，梯度更新会比较快；当梯度方向发生变化，此时会被惯性抵消，导致梯度比较缓慢，这样可以加快收敛，并减少震荡。

算法流程

1. 创建EMA平滑的shadow权重（对应EMA对象初始化和register方法）
2. 按照正常的训练流程，反向传播更新模型权重
3. 更新模型权重之后，再执行EMA平滑，更新shadow权重（对应update方法）
4. 重复2-3步，直到valid阶段
5. 备份模型权重，加载shadow权重，使用shadow权重进行模型的valid工作（对应apply_shadow方法）
6. 使用shadow权重作为模型权重，保存模型
7. 恢复模型权重（对应restore方法），继续重复以上步骤2-7

代码实现

按照以上算法流程，tensorflow和pytorch的实现思路基本是差不多的，上述流程中也列出与代码块的对应关系。

tensorflow版本

import tensorflow as tf


class EMA:

    def __init__(self, global_step: tf.Variable,
                 decay: float = 0.999):

        ema = tf.train.ExponentialMovingAverage(decay, global_step)

        vars_list = tf.trainable_variables()

        # EMA平滑操作
        self.ema_op = ema.apply(vars_list)

        # 原参数替换EMA平滑参数
        self.ema_assign_op = [tf.assign(w, ema.average(w)) for w in vars_list]

        # 用于临时存储原来的参数
        backup = [tf.get_variable('ema_backup/' + self._get_var_name(w.name), shape=w.shape, dtype=w.dtype, trainable=False) for w in vars_list]
        self.weight_copy_op = [tf.assign(w1, w2) for w1, w2 in zip(backup, vars_list)]

        # 恢复原参数
        self.weight_restore_op = [tf.assign(w1, w2) for w1, w2 in zip(vars_list, backup)]

        self.sess = None

    def _get_var_name(self, name):
        if name.endswith(":0"):
            name = name[:-2]
        return name

    def register(self, sess: tf.Session):
        """无需创建shadow变量，ema.apply(vars_list)会自动创建"""
        self.sess = sess

    def update(self):
        """EMA平滑操作，更新shadow权重"""
        self.sess.run(self.ema_op)

    def apply_shadow(self):
        """使用shadow权重作为模型权重，并创建原模型权重备份"""
        self.sess.run(self.weight_copy_op)
        self.sess.run(self.ema_assign_op)

    def restore(self):
        """恢复模型权重"""
        self.sess.run(self.weight_restore_op)

pytorch版本

import torch
import torch.nn as nn
from torch.utils.data import DataLoader


class EMA:
    def __init__(self, model: nn.Module,
                 decay: float = 0.999):
        self.model = model
        self.decay = decay
        self.shadow = {}
        self.backup = {}

    def register(self):
        """创建shadow权重"""
        for name, param in self.model.named_parameters():
            if param.requires_grad:
                self.shadow[name] = param.data.clone()

    def update(self):
        """EMA平滑操作，更新shadow权重"""
        for name, param in self.model.named_parameters():
            if param.requires_grad:
                assert name in self.shadow
                new_average = (1.0 - self.decay) * param.data + self.decay * self.shadow[name]
                self.shadow[name] = new_average.clone()

    def apply_shadow(self):
        """使用shadow权重作为模型权重，并创建原模型权重备份"""
        for name, param in self.model.named_parameters():
            if param.requires_grad:
                assert name in self.shadow
                self.backup[name] = param.data
                param.data = self.shadow[name]

    def restore(self):
        """恢复模型权重"""
        for name, param in self.model.named_parameters():
            if param.requires_grad:
                assert name in self.backup
                param.data = self.backup[name]
        self.backup = {}

Stochastic Weight Averaging (SWA)

相关论文：Averaging Weights Leads to Wider Optima and Better Generalization

摘要

深度神经网络模型一般都是使用随机梯度下降SGD（Stochastic Gradient Descent）来对损失进行优化，并联合学习率衰退，直到收敛。

作者发现简单得常规的SGD过程中，对多个权重点进行平均，这种方法称为Stochastic Weight Averaging（SWA），可以比传统的训练的到更好的泛化能力，并且在CIFAR-10、CIFAR-100、ImageNet这些数据的测试集中，对比state-of-the-art的残差网络模型，准确率都得到了提升。

介绍

《Loss Surfaces, Mode Connectivity, and Fast Ensembling of DNNs》提出了一种方法：Fast Geometric Ensembling (FGE)：可以在仅训练一个DNN，在权重空间采样多个临近的(最优)点，来进行集成来实现更好的性能。大体的思想就是训练一个DNN模型，在迭代过程选择表现最好的n个模型，然后使用这n个模型集成。

但作者发现使用FGE集成的网络权重都在最优解的周边，而将这些权重进行平均，可以得到更优秀的深度神经网络特征，对损失有着更好的几何理解，即Stochastic Weight Averaging（SWA）。

SWA和FGE其实都是集成的思想，但不同的是：

• FGE是模型空间的集成，即使用模型输出进行平均；
• SWA是在权重空间的集成，也就是模型权重(weight)的平均。

上图左可以看出，使用FGE集成的网络权重都在最优解的周边，如W1-W3。使用SWA的方法进行权重平均，可以得到更低的测试错误率；

上图中和右，表明了在相同的初始化下，SGD虽然比SWA可以取得更低的训练损失，但SWA却能够取得更低的测试错误率。

优点

对比常规的SGD和FGE，SWA可以在几乎不增加任何开销的情况下，提升模型的泛化性。主要包括以下几点：

• 周期性和固定的学习率SGD最终往往会在最优解周边徘徊，而无法更往最优解中心靠近，但使用SWA平均之后，可以更靠近最优的权重空间，如上图左所示；
• FGE虽然仅需训练一个模型，但在预测阶段，需要计算k个模型的输出，而SWA的预测阶段其实与SGD一样，仅需计算一次即可；
• SGD虽然比SWA可以取得更低的训练损失，但SWA却能够取得更低的测试错误率，如下图中和右所示；
• 对于训练损失，SGD是处于急剧上升的边缘，如下图右所示，$W_{SGD}$只要稍微往上移动一些，就会容易切换到更大的loss量级。这也是SWA可以提升泛化能力的一部分原因：训练loss处于比较平滑的方向；
• 在当时最先进的模型ResNet-50、DenseNet-161、ResNet150，仅使用SWA训练10个epoch就可以得到0.6%-0.8%的提升（ ImageNet数据集）

算法流程

其实，SWA的思想就很好理解，整体的算法流程也是比较简单。

首先，给定超参数

• 循环周期c，代表训练c步就使用SWA进行一次权重平均
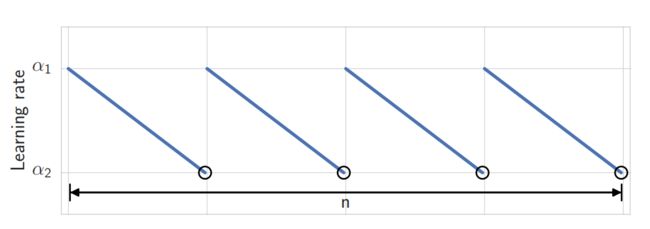
• 学习率${\alpha }_1,{\alpha }_2$，即周期学习率的上界和下界，论文的实验使用的周期性学习率如下图

然后，按照正常的SGD标准流程进行训练，每训练c步，就平均一次权重

最后，使用平均的权重$w_{SWA}$权重进行推理。

代码实现

在实际使用，更常见的做法是选择几个最优的模型checkpoint，手动对这几个checkpoint的权重进行平均，作为最终的模型。

tensorflow实现

import tensorflow as tf
import numpy as np


def apply_swa(checkpoint_list: list,
              weight_list: list,
              save_path: str,
              sess: tf.Session = None,
              strict: bool = True):
    """

    :param checkpoint_list: 要进行swa的模型路径列表
    :param weight_list: 每个模型对应的权重
    :param save_path: swa后的模型导出路径
    :param sess:
    :param strict: 是否需要完全匹配checkpoint的权重
    :return:
    """
    vars_list = tf.trainable_variables()
    saver = tf.train.Saver(var_list=vars_list)

    swa_op = []
    for var in vars_list:
        temp = []
        try:
            temp = [tf.train.load_variable(path, var.name) * w for path, w in zip(checkpoint_list, weight_list)]
        except tf.python.framework.errors_impl.NotFoundError:
            print(f"checkpoint don't match the model, var: '{var.name}' not in checkpoint")
            if strict:
                raise tf.python.framework.errors_impl.NotFoundError

        swa_op.append(tf.assign(var, np.sum(temp, axis=0)))

    if sess is None:
        sess = tf.Session()
    with sess.as_default() as sess:
        sess.run(swa_op)
        saver.save(sess, save_path)

pytorch实现

import torch
import torch.nn as nn


def apply_swa(model: nn.Module,
              checkpoint_list: list,
              weight_list: list,
              strict: bool = True):
    """

    :param model:
    :param checkpoint_list: 要进行swa的模型路径列表
    :param weight_list: 每个模型对应的权重
    :param strict: 输入模型权重与checkpoint是否需要完全匹配
    :return:
    """

    checkpoint_tensor_list = [torch.load(f, map_location='cpu') for f in checkpoint_list]

    for name, param in model.named_parameters():
        try:
            param.data = sum([ckpt['model'][name] * w for ckpt, w in zip(checkpoint_tensor_list, weight_list)])
        except KeyError:
            if strict:
                raise KeyError(f"Can't match '{name}' from checkpoint")
            else:
                print(f"Can't match '{name}' from checkpoint")

    return model

总结

1. EMA需要在每步训练时，同步更新shadow权重，但其计算量与模型的反向传播相比，成本很小，因此实际上并不会拖慢很对模型的训练进度；
2. SWA可以在训练结束，进行手动加权，完全不增加额外的训练成本；
3. 实际使用两者可以配合使用，可以带来一点模型性能提升。