极智AI | 量化实现分享五：详解格灵深瞳 EQ 量化算法实现

欢迎关注我的公众号 [极智视界]，回复001获取Google编程规范

  O_o   >_<   o_O   O_o   ~_~   o_O

  大家好，我是极智视界，本文剖析一下格灵深瞳 EQ (Easy Quant) 量化算法实现，以 Tengine 的实现为例。

  本文是模型量化实现分享的第五篇，前面已有四篇，有兴趣的同学可以查阅：

  (1) 《【模型推理】量化实现分享一：详解 min-max 对称量化算法实现》

  (2) 《【模型推理】量化实现分享二：详解 KL 对称量化算法实现》

  (3) 《【模型推理】量化实现分享三：详解 ACIQ 对称量化算法实现》

  (4)《【模型推理】量化实现分享四：Data-Free Quantization 香不香？详解高通 DFQ 量化算法实现》

  格灵深瞳 EQ 量化算法在论文《EasyQuant: Post-traning Quantization via Scale Optimization》中提出，EQ 量化算法有几个创新点：

  (1) 在 KLD 获得初始值后再用贪婪方式以最大化真实值&量化值间余弦相似度为优化目标，交替搜索权值 Scale 和 激活值 Scale；

  (2) 结合 Arm NEON 指令集优化，在 int7 量化时的性能表现更优。

  同样，这里不止会介绍原理，也会介绍实现。

  下面开始。

1、EQ 量化原理

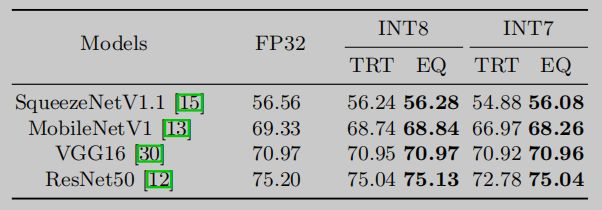
  先来看一下实验数据：

  这是 ImageNet2012 上分类模型的量化精度数据，对标 Nvidia TRT，可以看到 EQ 不管是在 int8 还是 int7 量化时表现均占优。再看一组检测模型的数据：

  以上是 SSD 目标检测模型在 VOC2007 上的量化精度 (mAP) 对比数据，同样可以看到 EQ 在 int8 & int7 量化效果占优。 以上两组数据还可以看出，EQ int7 接近 TRT int8 精度，所以有了下面这组性能对比数据 (总觉得少了组 EQ int8 的数据)：

  论文里还有其他的一些实验数据，如对比 QAT 量化感知训练的实验数据等，这里就不贴了，有兴趣的同学可以自行查阅。总结来说就是 EQ 算法在精度和性能上都是 yyds。

  来讲原理。

  首先量化的过程可以表示为：

  其中 X 为输入 tensor，S 为缩放因子，Clip 为裁剪，Round 为取整，所以量化的整个过程分为三步：

  (1) 裁剪；

  (2) 缩放；

  (3) 取整；

  这样的说法其实比较宏观，再细一点，可以把 S 分为激活值 S 和权值 S，那么第 l 层的量化过程就可以表示为：

  以上量化式是对于第 l 层来说的，再结合拓展到第 l + 1 层，会有 dequant / requant 的过程，整个逻辑就是这样的：

  量化过程很清晰直观，不再赘述。然后就到了 EQ 算法的精髓。

  EQ 是用余弦相似度来衡量真实值和量化值间的相似度，优化的目标是最大化余弦相似度，可以用如下式表达：

  EQ 的搜索策略是这样的：初始值 Sa 和 Sw 由 KLD 获得，在这个基础上搜索优化 Sa 和 Sw。搜索空间为 [αS, βS] 线性划分 n 个，先固定 Sa 优化 Sw，再固定 Sw 优化 Sa，两者交替进行直至设计的余弦相似度收敛或超时。对于整网来说，EQ 搜索策略如下 (这也是 EQ 量化的核心逻辑)：

  到这里原理已讲完，多说一句，前面可以看到论文实验结果对标 TRT，看了 EQ 的算法逻辑，应该很清楚，从精度上来说，EQ 根本不太可能会比 TRT 差，因为 TRT 是基于 KLD 量化的，而 EQ 是在 KLD 量化得出的 Scale 上再进一步搜索优化，结果怎么可能会弱于初始值 KLD 呢，所以精度数据那么好看也不用吃惊，这是理所当然的结果。另外一方面，，由于 EQ 是 KLD 后的二次优化，所以 EQ 的整个量化过程开销会比 KLD 量化大得多。

  到这里，主要说了精度为什么能涨点，还没说为什么能提速。这里我觉得论文是打了个擦边球，可以看到前面的性能数据对比对象是 TRT int8 vs EQ int7，这公平吗？直观来说确实不公平，不过再结合 EQ int7 精度接近 / 追平 TRT int8，再来看这个性能数据心里会平衡一些。这里也诞生了论文的一个创新点：既然前提我 int7 能做到 baseline int8 差不多的精度，那我就重心优化 int7 推理 (除非你 int7 精度比我 int7 高，不然我就用 int7 比你 int8，气死你~)。

  然后说一下为什么 int7 能提速。来看下图：

  在用 int8 量化时，中间数据一般用 int32 存储，直到 ARM V8.2-A 之前都没有能将两个 8bit 数据相乘的结果放到 32bit 寄存器的指令，替代的方法是用 SMLAL 将两个 8bit 数据相乘后存入 16bit 寄存器，再用 SADALP 合并两个 16bit 到 32bit 寄存器。对于一个常规卷积来说，用 int8 和 int7 的 NEON 乘法指令的次数差别如下：

• int8 推理：一次能算 ((2^15-1)/(27-1)^2) = 2 次 SMLAL；
• int7 推理：一次能算 ((2^15-1)/(26-1)^2) = 8 次 SMLAL；

  可以看到 int7 推理相比 int8 推理具有更加高效的乘法指令优化，这也正是 int7 推理效率更高的主要原因。

2、EQ 量化实现

  来看 EQ 量化的 tengine 实现。

  EQ 实现的主要代码如下：

case ALGORITHM_MM_EQ:
{
    if (quant_tool.scale_file.empty()){
        quant_tool.scale_file = "table_minmax.scale";
        quant_tool.activation_quant_tool();
    }
    /* Evaluate quantitative losses */
    if (quant_tool.evaluate){
        fprintf(stderr, "[Quant Tools Info]: Step Evaluate, evaluate quantitative losses\n");
        quant_tool.assess_quant_loss(0);
    }
    /* Enable EQ search */
    fprintf(stderr, "[Quant Tools Info]: Step Search, enable EQ search\n");
    quant_tool.quant_search();
    quant_tool.model_file = "save_i8_eq.tmfile";
    save_graph_i8_perchannel(quant_tool.model_file.c_str(), quant_tool.scale_file.c_str(), quant_tool.output_file, quant_tool.inplace, true);
    break;
}

  这里的主逻辑和论文里的稍微有一些出入，论文里的 EQ 搜索初始值是 KLD 得出的，而这里是 MIN-MAX 得出的。在得到 MIN-MAX 出来的 Scale 初始值后进行 EQ 的搜索，主要是这个接口：

quant_tool.quant_search();

  在这个接口里主要有两个逻辑：

  (1) 当层类型为 CONV 或 FC 时：先进行权值 Scale 的搜索 requant，再进行偏置 requant，再进行激活值 requant，最后计算余弦相似度；

  (2) 当层类型非 CONV 及 FC 时：不进行搜索也不进行权值&偏置 requant，直接进行激活值 requant，并计算余弦相似度；

  可以看到和论文里的逻辑还是不太一样，这里只进行了权值 Scale 的搜索，搜索空间为 [1.3/200 Scale, 1.3/200x201 Scale]，迭代间隔 1.3/20。下面来看代码：

if (this->op_name == OP_CONV || this->op_name == OP_FC)    /// 当层类型为CONV或FC时
{
    this->gen_weight_scale(this->weight_tensor_fake_quant, this->weight_data_fake_quant, this->weight_tensor_fake_quant->elem_num, 8, 1, weight_tensor_fake_quant->dims[0]);
    this->gen_weight_scale(this->weight_tensor_fp32, this->weight_data_fp32, this->weight_tensor_fp32->elem_num, 8, 1, weight_tensor_fp32->dims[0]);

    std::vector<double> cosin_save(weight_tensor_fake_quant->dims[0], -1);
    std::vector<float> zoom_save(weight_tensor_fake_quant->dims[0], -1);
    for (int snum = 0; snum < 201; snum = snum + 20){     /// 搜索空间
        float zoom = 1.3 / 200 * (snum + 1);
        /* step 0 weight requant */
        if (snum < 200)
            this->weight_requant_search(weight_tensor_fake_quant, weight_data_fake_quant, weight_tensor_fake_quant->elem_num, 8, 1, weight_tensor_fake_quant->dims[0], zoom);
        else{
            this->weight_requant_search(weight_tensor_fake_quant, weight_data_fake_quant, weight_tensor_fake_quant->elem_num, 8, 1, weight_tensor_fake_quant->dims[0], zoom_save.data());
            float* buf = (float*)sys_malloc(weight_tensor_fake_quant->dims[0] * 4);
            memcpy(buf, zoom_save.data(), weight_tensor_fake_quant->dims[0] * 4);
          
            for (int bi = 0; bi < weight_tensor_fake_quant->dims[0]; bi++){
                buf[bi] *= weight_tensor_fp32->scale_list[bi];
            }

            weight_tensor_fp32->scale_list = buf;
            weight_tensor_fp32->quant_param_num = weight_tensor_fp32->dims[0];
        }
        if (interleave_size_fake != 0){
            int M = weight_tensor_fake_quant->dims[0];
            int K = weight_tensor_fake_quant->elem_num / weight_tensor_fake_quant->dims[0];
            this->conv_hcl_interleave_pack4_fp32(M, K, weight_data_fake_quant, interleave_buffer_fake_quant);
        }

        /* step 1 bias requant */
        if (node_fake_quant->ir_node->input_num > 2){
            struct tensor* input_tensor_fake_quant = graphn_fake_quant->tensor_list[node_fake_quant->ir_node->input_tensors[0]];
            struct tensor* bias_tensor_fake_quant = graphn_fake_quant->tensor_list[node_fake_quant->ir_node->input_tensors[2]];
            struct tensor* bias_tensor_fp32 = graphn_fp32->tensor_list[node_fp32->ir_node->input_tensors[2]];

            bias_size = bias_tensor_fp32->elem_num * bias_tensor_fp32->elem_size;
            bias_data_fp32 = (float*)bias_tensor_fp32->data;
            bias_data_fake_quant = (float*)bias_tensor_fake_quant->data;
            this->bias_requant(input_tensor_fake_quant, weight_tensor_fake_quant, bias_tensor_fake_quant, bias_data_fake_quant, bias_tensor_fake_quant->elem_num, bias_tensor_fake_quant->dims[0]);
        }

        /* step 2 activation requant */
        for (int imgi = 0; imgi < this->max_search_img_num; imgi++){
            this->set_node_input_output_tensor(i, imgi, snum);
            /* FP32 op run */
            if (snum == 0){
                node_ops_fp32->run(node_ops_fp32, node_fp32, exec_graph_fp32);
                this->execidx_elemnum[i] = output_tensor_fp32->elem_num;   //exec idx --> output elem num
                this->execidx_elemsize[i] = output_tensor_fp32->elem_size; //exec idx --> output elem size
                this->execidx_nodename[i] = output_tensor_fp32->name;
            }

            /* fake quant op run */
            node_ops_fake_quant->run(node_ops_fake_quant, node_fake_quant, exec_graph_fake_quant);
            this->activation_requant(out_imgs_fake_quant[imgi].data(), output_tensor_fake_quant->elem_num, 8, 1, output_tensor_fake_quant->scale, output_tensor_fake_quant->zero_point);
        } 

        output_channel = output_tensor_fp32->dims[1];
 		
        /* step 3 cal cosin_similarity */
        if (this->op_name == OP_CONV || (this->op_name == OP_FC && this->max_search_img_num > 1))
            this->cosin_similarity(this->cosin, this->out_imgs_fp32, this->out_imgs_fake_quant, this->max_search_img_num, this->execidx_elemnum[i], output_channel);
        else
            this->cosin_similarity(this->cosin, this->out_imgs_fp32, this->out_imgs_fake_quant, this->max_search_img_num, this->execidx_elemnum[i], 1);

        for (int cosi = 0; cosi < output_channel; cosi++){
            if (cosin[cosi] > cosin_save[cosi]){
                cosin_save[cosi] = cosin[cosi];
                zoom_save[cosi] = zoom;}
        }
        if (snum == 200){
            if (this->op_name == OP_CONV || (this->op_name == OP_FC && this->max_search_img_num > 1))
                this->print_cosin(this->cosin.data(), i, output_channel);
            else
                this->print_cosin(this->cosin.data(), i, 1);
        }

        if (op_name == OP_CONV || op_name == OP_FC){
            memcpy(weight_data_fake_quant, weight_data_fp32, weight_size);
          
            memcpy(interleave_buffer_fake_quant, interleave_buffer_fp32, interleave_size_fake);
            if (node_fake_quant->ir_node->input_num > 2){
                memcpy(bias_data_fake_quant, bias_data_fp32, bias_size);}}}
}
else{
    /* per image run */
    for (int imgi = 0; imgi < this->max_search_img_num; imgi++){
        this->set_node_input_output_tensor(i, imgi, 0);
        node_ops_fp32->run(node_ops_fp32, node_fp32, exec_graph_fp32);
      
        /* step 0 activation requant */
        node_ops_fake_quant->run(node_ops_fake_quant, node_fake_quant, exec_graph_fake_quant);
        this->activation_requant(out_imgs_fake_quant[imgi].data(), output_tensor_fake_quant->elem_num, 8, 1, output_tensor_fake_quant->scale, output_tensor_fake_quant->zero_point);

        this->execidx_elemnum[i] = output_tensor_fp32->elem_num;   //exec idx --> output elem num
        this->execidx_elemsize[i] = output_tensor_fp32->elem_size; //exec idx --> output elem size
        this->execidx_nodename[i] = output_tensor_fp32->name;
    }
  	/* step 1 cal cosin_similarity */
    this->cosin_similarity(this->cosin, out_imgs_fp32, out_imgs_fake_quant, this->max_search_img_num, this->execidx_elemnum[i], 1);
    this->print_cosin(this->cosin.data(), i, 1);
    this->execidx_loss[i] = cosin;
}

  这样就完成了 EQ 算法的搜索过程。

  以上详细分享了格灵深瞳 EQ 算法的原理和实现，希望我的分享能对你的学习有一点帮助。

 【公众号传送】

《【模型推理】量化实现分享五：详解格灵深瞳 EQ 量化算法实现》

扫描下方二维码即可关注我的微信公众号【极智视界】，获取更多AI经验分享，让我们用极致+极客的心态来迎接AI ！