线性代数学习笔记11-1：总复习Part1（CR分解、LU分解、QR分解）

引用：MIT线性代数_2020年更新讲解课程

下面的一系列分解，涉及了线性代数中的各个重要知识点：

关于求解方程组的分解：

• Ch1[矩阵乘法角度] 矩阵$\mathbf{A}$=列向量矩阵$\mathbf{C}$和行向量矩阵$\mathbf{R}$的乘积
• Ch2[消元解方程组] LU分解
• Ch3[施密特正交化] QR分解：将列向量线性无关的矩阵$\mathbf{A}$，转为正交矩阵$\mathbf{Q}$，且$\mathbf{R}$必为上三角阵

关于特征值/特征向量/奇异值的分解：

• Ch5[相似对角化] 得到特征值和特征向量后，矩阵$\mathbf{A}$相似于以特征值为对角元的对角阵$\mathbf{\Lambda }$
• Ch4[对称矩阵] 对称矩阵$\mathbf{S}$具有正交的特征向量，对角化得到$\mathbf{S}=\mathbf{Q}\mathbf{\Lambda }{\mathbf{Q}}^T$
• CH6[奇异值分解（“广义对角化”操作）] 任意矩阵可分解为$\mathbf{A}=\mathbf{U}\mathbf{\Sigma }{\mathbf{V}}^T$，其中$\mathbf{\Sigma }$中左上角的对角阵对应将行空间中的标准正交基映射到列空间的标准正交基（$\mathbf{A}{\mathbf{v}}_i={\sigma }_i{\mathbf{u}}_i$，这类似于找出特征值和特征向量）；$\mathbf{\Sigma }$中其余部分为0元素，对应$\mathbf{A}$的零空间中的一组正交基

Ch1. 矩阵乘法与CR分解

矩阵乘法的理解

首先，矩阵向量乘法，可以视为矩阵的列向量的线性组合；

如图$\left[\begin{array}{lll}1& 4& 5\\ 3& 2& 5\\ 2& 1& 3\end{array}\right]\left[\begin{array}{l}{x}_1\\ x_2\\ x_3\end{array}\right]$，可以视为系数为$x_1,x_2,x_3$的线性组合

列空间与秩

尝试所有可能的列向量线性组合（$x_1,x_2,x_3$），能够得到列空间$C(\mathbf{A})$（即列向量的张成空间）

列空间$C(\mathbf{A})$的维度=列空间的基向量个数=$\mathbf{A}$的秩

例如上面的矩阵$\mathbf{A}=\left[\begin{array}{lll}1& 4& 5\\ 3& 2& 5\\ 2& 1& 3\end{array}\right]$只有一列、二列是无关的，而第三列是前两列之和
因此，$\mathbf{A}$的秩为2，对应$C(\mathbf{A})$是二维平面，列空间只有两个基向量（例如选取$\mathbf{A}$的第一/二列，即可得到一组基）；

另外，在求解方程$\mathbf{Ax}=0$时，我们还引入零空间的概念：即$\mathbf{Ax}=0$的所有可能解$\mathbf{x}$构成的空间
对于m x n 的秩为r的矩阵，其零空间的维度为$n-r$，即零空间有$n-r$个基向量（并且这些基向量通过消元后的自由列给出）

CR分解（矩阵的行与列的关系）

CR分解：$\mathbf{A}=\mathbf{CR}$，其中：

• $\mathbf{C}$的列线性无关，$\mathbf{C}$的列向量（$r$个）就是$\mathbf{A}$的列空间（$r$维）的一组基（$r$个）
• $\mathbf{R}$的行线性无关，$\mathbf{R}$的行向量（$r$个）就是$\mathbf{A}$的行空间（$r$维）的一组基（$r$个）
  并且，$\mathbf{R}$就是$\mathbf{A}$的行简化阶梯型，$\mathbf{R}$中包含一个$r$阶单位阵$\mathbf{I}$（见下面的理解1）

理解1：
$\mathbf{C}$的列向量为$\mathbf{A}$列空间的一组基 ，$\mathbf{R}$指出如何从$\mathbf{C}$的列向量线性组合得到$\mathbf{A}$
（例如上面，$\mathbf{C}$只保留了$\mathbf{A}$中无关的第一列、第二列；
$\mathbf{R}$第一列10对应$\mathbf{A}$的第一列，$\mathbf{R}$第二列01对应$\mathbf{A}$的第二列（可见$\mathbf{R}$中必然含有单位阵$\mathbf{I}$ ps. 不考虑列的出现顺序的问题），$\mathbf{R}$第三列11对应$\mathbf{A}$的第三列，因为$\mathbf{A}$的第三列为$\mathbf{C}$的

理解2：
对称的，也可以从向量右乘矩阵的角度，将CR分解视为：
在$\mathbf{R}$中保留行空间的一组基，用$\mathbf{C}$（的每一行）对$\mathbf{R}$的行向量做线性组合

CR分解展示了：任意矩阵的行秩=列秩（行空间的维数=列空间的维数）

证明：
由上可知，CR分解中，$\mathbf{C}$可视为保留了$\mathbf{A}$列空间的一组基；$\mathbf{R}$可视为保留了$\mathbf{A}$行空间的一组基
又因为$\mathbf{A}=\mathbf{CR}$，根据矩阵乘法规则，$\mathbf{C}$的列数=$\mathbf{R}$的行数
这就是说，行空间和列空间维数相等，行秩=列秩

关于CR分解$\mathbf{A}=\mathbf{CR}$的小结：

• $\mathbf{C}$中的列直接由$\mathbf{A}$中的无关列向量给出
• 实际上$\mathbf{R}$就是$\mathbf{A}$的行简化阶梯型
• $\mathbf{C}$可视为保留了$\mathbf{A}$列空间的一组基；$\mathbf{R}$可视为保留了$\mathbf{A}$行空间的一组基
  $\mathbf{R}$指出如何将$\mathbf{C}$列向量线性组合得到$\mathbf{A}$；$\mathbf{C}$指出如何将$\mathbf{R}$行向量线性组合得到$\mathbf{A}$
• 由$\mathbf{A}=\mathbf{CR}$的乘法约束，可以得出行空间的基向量个数=列空间基向量个数，即行秩=列秩

CR分解的问题：

• 难以处理，不是大型计算的最佳选择
• 当$\mathbf{A}$为可逆方阵，所有列线性无关（$\mathbf{C}$就是$\mathbf{A}$本身），此时$\mathbf{A}=\mathbf{CR}$变为$\mathbf{A}=\mathbf{AI}$（什么也没得到）

秩1矩阵、列向量乘以行向量

根据“行秩=列秩”的结论，可以进一步推论：
当矩阵只有一个线性无关的行向量时，必然也只有一个线性无关列向量，此即秩1矩阵：

• 所有行/列 都是 第一行/第一列 的倍数；
• 进而，$\mathbf{A}=\mathbf{CR}$中，$\mathbf{C}$和$\mathbf{R}$退化为列向量和行向量
  

秩1矩阵是线性代数的基石Building Block，复杂的矩阵可以拆解为秩1矩阵

如图，通常将矩阵乘法理解为“行向量乘以列向量，得到结果中的一个元素”
这里，我们反而理解为“列向量乘以行向量（外积），得到一个秩1矩阵即 $b_i{c}_i^{\ast }$，各个秩1矩阵叠加得到结果”

Ch2. 解方程组、LU分解与四个子空间

先研究齐次方程组$\mathbf{Ax}=0$，再研究非齐次方程组$\mathbf{Ax}=\mathbf{b}$

消元法与LU分解

消元法解方程的过程如下：核心是不断减少某一行方程中的未知量个数

用矩阵乘法表示消元过程，就是LU分解$\mathbf{A}=\mathbf{LU}$（需要行交换时，变为$\mathbf{PA}=\mathbf{LU}$）

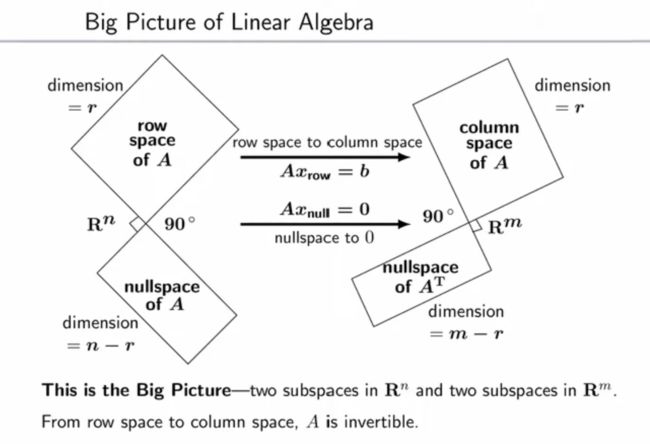
四个字空间

方程组$\mathbf{Ax}=0$的所有可能解构成了零空间$N(\mathbf{A})$，维度$n-r$

并且，行空间$C({\mathbf{A}}^T)$与零空间$N(\mathbf{A})$互为正交补

原因：
对于方程组$\mathbf{Ax}=0$，第一种理解是：用$\mathbf{x}$对$\mathbf{A}$的列向量做线性组合；
这里使用另一种理解：$\mathbf{A}$的每一行与$\mathbf{x}$做点积，结果为0，这就是说，所有行向量与$\mathbf{x}$正交，从而行空间与零空间正交

同理，将矩阵转置后，研究${\mathbf{A}}^T\mathbf{x}=0$，也可得出：列空间$C(\mathbf{A})$与左零空间$N({\mathbf{A}}^T)$互为正交补

由此，整个${\mathbf{R}}^n$空间和${\mathbf{R}}^m$空间，可以分别拆解为一对子空间，关系如图：

• 对于行空间中的$\mathbf{x}$，$\mathbf{Ax}=\mathbf{b}$，这是将行空间投影到列空间（$\mathbf{Ax}$就是用行空间的向量${\mathbf{x}}_{row}$对$\mathbf{A}$的列向量做线性组合，结果位于列空间中）
• 对于零空间中的$\mathbf{x}$，$\mathbf{Ax}=0$，这是将零空间投影到零向量（而不是左零空间）（$\mathbf{Ax}$就是用行空间的向量${\mathbf{x}}_{row}$对$\mathbf{A}$的列向量做线性组合，结果位于列空间中）
• 将行空间投影到列空间$\mathbf{Ax}=\mathbf{b}$是可逆的，而$\mathbf{Ax}=0$则不可逆，这就是为什么说“零空间的存在（维度>0）会导致矩阵不可逆”，详见「伪逆」部分的笔记

Ch3. 正交化、QR分解和最小二乘法

正交向量

正交Orthogonal可以理解为垂直Perpendicular的高级说法

向量的正交，就是内积为0：${\mathbf{x}}^T\mathbf{y}=0$
${\mathbf{x}}^T\mathbf{x}={\Vert \mathbf{x}\Vert }^2$ 则对应了向量本身模长的平方

正交矩阵

正交矩阵$\mathbf{Q}$的列向量构成一组标准正交基（各个基向量相互正交，模长为1）

正交矩阵$\mathbf{Q}$的性质：

• 正交矩阵$\mathbf{Q}$的逆矩阵${\mathbf{Q}}^{-1}={\mathbf{Q}}^T$
  原因：标准正交基满足${\mathbf{q}}_i^T{\mathbf{q}}_i=1，{\mathbf{q}}_i^T{\mathbf{q}}_j=0$ ，故正交矩阵$\mathbf{Q}$满足${\mathbf{Q}}^T\mathbf{Q}=\mathbf{Q}{\mathbf{Q}}^T=\mathbf{I}$

ps. 上图中①为正交矩阵，有$\mathbf{Q}$满足${\mathbf{Q}}^T\mathbf{Q}=\mathbf{Q}{\mathbf{Q}}^T=\mathbf{I}$；
而②并不是真正的正交矩阵（只有两列，不是方阵），但由于各个列向量标准正交，仍有${\mathbf{Q}}^T\mathbf{Q}=\mathbf{I}$
另外，虽然②中$\mathbf{Q}{\mathbf{Q}}^T\ne \mathbf{I}$，但这个$\mathbf{Q}{\mathbf{Q}}^T$仍为一种投影矩阵（因为多次相乘，仍得到它本身）

• 正交矩阵$\mathbf{Q}$几何上对应单纯的旋转
  进而，任意正交矩阵的乘积${\mathbf{Q}}_1{\mathbf{Q}}_2$仍为正交矩阵
• 正交矩阵与向量相乘，不改变其长度
• 正交矩阵$\mathbf{Q}$特征值满足$|\lambda |=1$（可能为复数）

Gram-Schmidt正交化和QR分解

对于矩阵$\mathbf{A}$（前提：各个列向量线性无关），我们希望使其列向量${\mathbf{a}}_1...{\mathbf{a}}_n$变为正交的列向量${\mathbf{q}}_1...{\mathbf{q}}_n$，且各个列向量的模长标准化为1，这就是Gram-Schmidt正交化

用矩阵形式表达，就是QR分解$\mathbf{A}=\mathbf{QR}$，其中$\mathbf{R}={\mathbf{Q}}^T\mathbf{A}$为上三角阵

例如，原来的列向量${\mathbf{a}}_1=r_{11}{\mathbf{q}}_1$（第一个基向量，只需要标准化，$r_{11}=\Vert {\mathbf{a}}_1\Vert$）
而${\mathbf{a}}_2=r_{12}{\mathbf{q}}_1+r_{22}{\mathbf{q}}_2$（原来的第二个基向量，是标准化后的第一个/第二个基向量的线性组合）

仍然可以从秩1矩阵的角度入手，将QR分解进一步分解为若干秩1矩阵

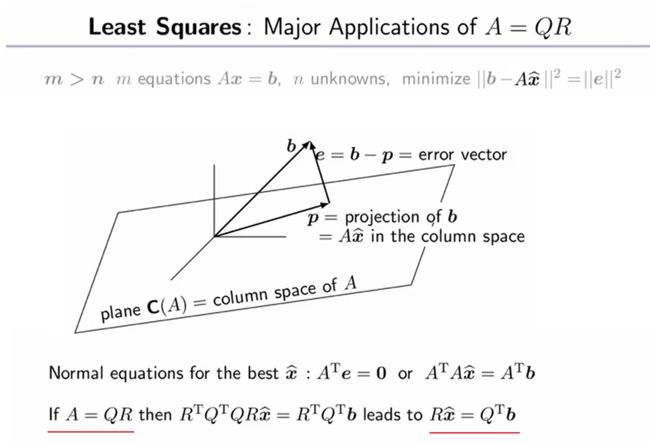
最小二乘法：QR分解的主要应用

当$\mathbf{Ax}=\mathbf{b}$的方程个数过多时（$m>n$，行数大于未知量个数），意味着约束条件过多
此时，$\mathbf{A}$的列空间只是整个${\mathbf{R}}^m$空间中的一个平面，然而$\mathbf{b}$极有可能不在这个平面内，此时方程无解

我们将$\mathbf{b}$投影到$\mathbf{A}$的列空间内，从而寻找最优的近似解$\hat{\mathbf{x}}$（此时误差$\Vert \mathbf{e}{\Vert }^2=\Vert \mathbf{b}-\mathbf{A}\hat{\mathbf{x}}{\Vert }^2$最小）

• 可以体会到${\mathbf{A}}^T$矩阵的重要性：
  同时乘以${\mathbf{A}}^T$，能让$\mathbf{Ax}=\mathbf{b}$变得有解
  乘以${\mathbf{A}}^T$，任意矩阵$\mathbf{A}$变为方阵${\mathbf{A}}^T\mathbf{A}$（至少半正定）
• 若有$\mathbf{A}=\mathbf{QR}$，最小二乘法写为$\mathbf{R}\hat{\mathbf{x}}={\mathbf{Q}}^T\mathbf{b}$
  这就是说，将$\mathbf{A}$的列向量标准正交化后，求解最小二乘变得更加容易