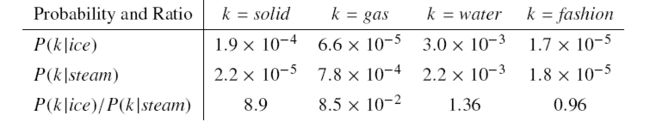NLP模型(二)——GloVe介绍
文章目录
- 1. GloVe模型简述
- 2. 共现矩阵
- 3. 共现概率
- 4. 共现概率比
- 4. GloVe算法
- 5. 损失函数
- 6. 得出结果
1. GloVe模型简述
获取词向量基本上有两种思路:
- 利用全局统计信息,进行矩阵分解(如LSA)来获取词向量,这样获得的词向量往往在词相似性任务上表现不好,表明这是一个次优的向量空间结构;
- 利用局部上下文窗口单独训练,比如前面的word2vec算法,但是统计信息作为有用的先验知识,没有很好的利用到。
前面我们介绍了word2vec模型,并对 S k i p − g r a m Skip-gram Skip−gram 算法进行了实现,但是,尽管word2vec在学习词与词间的关系上有了大进步,它却有很明显的缺点:只能利用一定窗口长度的上下文环境,即利用局部信息,没法利用整个语料库的全局信息。基于此,GloVe 模型诞生了,它的全称是 g l o b a l v e c t o r global \hspace{0.5em} vector globalvector,其目的就是改进对word2vec的这个缺点进行改进,运用到全局的语料信息。
2. 共现矩阵
想要捕捉全文的语义信息,这就不得不提共现矩阵了。共现矩阵反映了在预料库中,中心词与关联词的关联程度,这是一种基于统计的方法。首先创建一个窗口大小,与word2vec一样,使得窗口不断的滑动并得到中心词与背景词的关联程度,出现在同一个窗口关联程度+1,创建一个全局的词表矩阵来记录所有的关联程度。
这里用一个例子来说明共现矩阵的创建。
比如下面的词语:
T o b e o r n o t t o b e , t h a t i s q u e s t i o n . To \hspace{0.5em} be \hspace{0.5em} or \hspace{0.5em} not \hspace{0.5em} to \hspace{0.5em} be, that \hspace{0.5em} is \hspace{0.5em} question. Tobeornottobe,thatisquestion.
假设我们已经对其标点符号及大小写进行了处理(统一小写),这里我们设置窗口长度为1,即窗口左边长为1,右边长为1,窗口如下:

以 t o to to 为中心时,一同出现的有 b e be be,则矩阵中坐标为 ( t o , b e ) (to, be) (to,be) 的共现数+1,窗口不断滑动,我们设共现矩阵中一行为中心词,一列代表背景词,则最后的共现矩阵如下:
| words | to | be | or | not | that | is | question |
|---|---|---|---|---|---|---|---|
| to | 0 | 2 | 0 | 1 | 0 | 0 | 0 |
| be | 2 | 0 | 1 | 0 | 1 | 0 | 0 |
| or | 0 | 1 | 0 | 1 | 0 | 0 | 0 |
| not | 1 | 0 | 1 | 0 | 0 | 0 | 0 |
| that | 0 | 1 | 0 | 0 | 0 | 1 | 0 |
| is | 0 | 0 | 0 | 0 | 1 | 0 | 1 |
| question | 0 | 0 | 0 | 0 | 0 | 1 | 0 |
共现矩阵很明显是一个对称矩阵,为什么说共现矩阵是基于全局语料信息的矩阵呢?共现矩阵的构建需要遍历全文,存储了全文中几个词之间的关联程度,这里存储了全文中的几个词取决于窗口的大小。
3. 共现概率
有了共现矩阵,我们就可以做很多事情了,最典型的就是潜在语义分析(LSA)算法,对其进行奇异值分解以及截断奇异值分解,得到相应的矩阵,当然这里并不使用这些,这里我们要用到的是共现概率。
设共现矩阵中的元素为 x i j x_{ij} xij,则定义共现概率如下:
P ( x i j ) = P ( w o r d j ∣ w o r d i ) = x i j x i P(x_{ij})=P(word_j|word_i)=\frac{x_{ij}}{x_i} P(xij)=P(wordj∣wordi)=xixij其中 x i x_i xi 为共现矩阵中以 w o r d i word_i wordi 为中心词的所有出现频次,计算式为 x i = ∑ k = 0 N x i k x_i=\sum_{k=0}^Nx_{ik} xi=∑k=0Nxik,整个式子也很好理解,即所有以 w o r d i word_i wordi 为中心词的窗口中 w o r d j word_j wordj 出现的概率。
4. 共现概率比
词的共现次数与其语义的相关性往往不是严格成比例,所以直接用共线性来表征词之间相关性效果不好,因此,作者通过引入第三个词,通过词之间的差异来刻画相关性。词之间的差异选择用两个词与同一个词的共现概率的次数来更好的判断词之间的相关性。
设三个单词为 w i , w j , w k w_i,w_j,w_k wi,wj,wk,则共现概率比表示如下:
p ( w k ∣ w i ) p ( w k ∣ w j ) = p i k p j k = x i k x i x j k x j \frac{p(w_k|w_i)}{p(w_k|w_j)}=\frac{p_{ik}}{p_{jk}}=\frac{\frac{x_{ik}}{x_i}}{\frac{x_{jk}}{x_j}} p(wk∣wj)p(wk∣wi)=pjkpik=xjxjkxixik下面我用论文中的例子来对共现概率比进行一个解释。
- 首先看第一行 P ( k ∣ i c e ) P(k|ice) P(k∣ice), i c e ice ice是冰,当 k = s o l i d k=solid k=solid 时,其概率大于第二行的 P ( k ∣ s t e a m ) P(k|steam) P(k∣steam),这是很正常的;
- 然后看第三行 P ( k ∣ i c e ) / P ( k ∣ s t e a m ) P(k|ice)/P(k|steam) P(k∣ice)/P(k∣steam),当 k = s o l i d k=solid k=solid 时,由于 s o l i d solid solid 与 i c e ice ice 的相关程度更高,所以比值大于1;
- 在第三行中,当 k = g a s k=gas k=gas 时,由于 g a s gas gas 与 s t e a m steam steam 的相关程度更高,所以比值小于1;
- 在第三行中,当 k = w a t e r k=water k=water 时,由于 w a t e r water water 与 i c e , s t e a m ice,steam ice,steam 都有关,所以比值在1的附近,当 k = f a s h i o n k=fashion k=fashion 时,由于 f a s h i o n fashion fashion 与 i c e , s t e a m ice,steam ice,steam 都无关,所以比值也在1的附近。
所以,我们想训练的目的就很明显了,我们需要做的就是让这三词的词向量去满足这个共现概率比,与分母有关的比值比1高,与分子更有关的比值比1小,与分子分母都有关或都无关的比值维持在1附近。
4. GloVe算法
结合上面的共现概率比,设中心词的词向量为 v i , v j v_i,v_j vi,vj,关联的背景向量为 u k u_k uk,所以我们就是要找到一种映射关系 f f f,使得
f ( v i , v j , u k ) = p i k p j k f(v_i,v_j,u_k)=\frac{p_{ik}}{p_{jk}} f(vi,vj,uk)=pjkpik由于 v i , v j , u k v_i,v_j,u_k vi,vj,uk 为向量,右边的概率为标量,向量经过运算得到一个标量,那只能是经过内积运算了,内积肯定是 v , u v,u v,u 向量之间的内积,但是 v v v 向量有两个,这怎么处理呢?
作者使用的是两个中心词向量的差来与背景词向量进行内积,如下
f ( ( v i − v j ) T u k ) = f ( v i T u k − v j T u k ) = p i k p j k f((v_i-v_j)^Tu_k)=f(v_i^Tu_k-v_j^Tu_k)=\frac{p_{ik}}{p_{jk}} f((vi−vj)Tuk)=f(viTuk−vjTuk)=pjkpik因为中心词向量的差可以去除共线性,即取出向量中的相似关系。
再对上式进行观察,左边是差 v i T u k − v j T u k v_i^Tu_k-v_j^Tu_k viTuk−vjTuk,而右边是分式,差转为分式,很容易想到使用指数的形式,因为 e a − b = e a ⋅ e − b = e a / e b e^{a-b}=e^a \cdot e^{-b}={e^a}/{e^b} ea−b=ea⋅e−b=ea/eb,刚好是分式的形式,所以,将其设为映射 f f f 可得
f ( v i T u k − v j T u k ) = e v i T u k − v j T u k = p i k p j k f(v_i^Tu_k-v_j^Tu_k)=e^{v_i^Tu_k-v_j^Tu_k}=\frac{p_{ik}}{p_{jk}} f(viTuk−vjTuk)=eviTuk−vjTuk=pjkpik即
e v i T u k = p i k e^{v_i^Tu_k}={p_{ik}} eviTuk=pik两边同时取对数消除指数得到
v i T u k = log p i k = log x i k x i = log x i k − log x i \begin{aligned} v_i^Tu_k&=\log p_{ik} \\ &=\log{\frac{x_{ik}}{x_i}} \\ &=\log x_{ik} - \log x_i \end{aligned} viTuk=logpik=logxixik=logxik−logxi这样就找到了一种映射满足右边的分式了。
但是,这还没有完成!向量的内积是可以交换顺序的,即 v i T u k = u k T v i v_i^Tu_k=u_k^Tv_i viTuk=ukTvi,如果使用上面的式子的话,得到的是
v i T u k = u k T v i log x i k − log x i = log x k i − log x k log x i = log x k \begin{aligned} v_i^Tu_k&=u_k^Tv_i \\ \log x_{ik} - \log x_i&=\log x_{ki} - \log x_k \\ \log x_i&=\log x_k \end{aligned} viTuklogxik−logxilogxi=ukTvi=logxki−logxk=logxk因为共现矩阵是对称矩阵,所以 x k i = x i k x_{ki}=x_{ik} xki=xik,故得到 log x i = log x k \log x_i=\log x_k logxi=logxk,但是,这个式子明显不是恒等式,所以这个公式的推导并不能成立。
作者在论文中对上述公式进行了改写,改为
v i T u k = log x i k − b i − b k v_i^Tu_k=\log x_{ik} - b_i-b_k viTuk=logxik−bi−bk这样式子就能很好的满足交换后依然相等的性质,这里的 b i , b k b_i,b_k bi,bk 为偏置常数,是可学习的参数。
5. 损失函数
上面共现概率比是一个标量,我们也是将向量通过表达式转为标量来进行的训练,这样,相当于就是一个回归问题,那么很自然的就可以使用均方差作为损失函数,损失如下:
l o s s = ∑ i , k ( v i T u k + b i + b k − log x i k ) 2 loss=\sum_{i,k}(v_i^Tu_k + b_i+b_k-\log x_{ik})^2 loss=i,k∑(viTuk+bi+bk−logxik)2哈佛大学的语言学家乔治·金斯利·齐夫( G e o r g e K i n g s l e y Z i p f George \hspace{0.5em}Kingsley\hspace{0.5em} Zipf GeorgeKingsleyZipf)于1949年发表的齐夫定律( Z i p f ′ s l a w Zipf's \hspace{0.5em} law Zipf′slaw)表述为:在自然语言的语料库里,一个单词出现的频率与它在频率表里的排名成反比。
根据齐夫定律,高频词往往携带的信息较少,而低频词往往携带较多的信息。若损失函数这样设置,将会使得模型趋于高频词,所以作者加了一个惩罚系数 f ( x i k ) f(x_{ik}) f(xik),使得损失如下
l o s s = ∑ i , k f ( x i k ) ( v i T u k + b i + b k − log x i k ) 2 loss=\sum_{i,k}f(x_{ik})(v_i^Tu_k + b_i+b_k-\log x_{ik})^2 loss=i,k∑f(xik)(viTuk+bi+bk−logxik)2 f ( x i k ) f(x_{ik}) f(xik) 表达式如下
f ( x ) = { ( x x m a x ) α , x ≤ x m a x 1 , o t h e r w i s e f(x)=\left\{ \begin{aligned} &(\frac{x}{x_{max}})^{\alpha},&x \le x_{max}\\ &1,&otherwise \end{aligned} \right. f(x)=⎩⎨⎧(xmaxx)α,1,x≤xmaxotherwise其中 x m a x x_{max} xmax 的为一个超参数,表示一个阈值,即词出现的次数,超过 x m a x x_{max} xmax 即为高频词,其次数 α \alpha α 也是超参数,作者选取的是word2vec中的0.75。这样的表达能够对高频的惩罚多一些,而减少对低频次的惩罚。
6. 得出结果
照上面的方法训练,可以得到两个词向量矩阵,即中心词向量矩阵 V V V 和背景词向量矩阵 V V V ,word2vec模型只拿了其中一个矩阵来进行作为最终的词向量,作者的做法是将其进行相加,即
r i = u i + v i r_i=u_i+v_i ri=ui+vi其中 r i r_i ri 为最终使用的词向量矩阵 R R R 中的元素。