Java二叉树的构造与三种非递归遍历算法

二叉树的非递归遍历可以依赖于栈结构解决。其中先序和中序遍历思路较为相似，后序遍历需要另外设置一个访问位变量，比前两种较为复杂一些。

首先是二叉树的构造，这里使用二叉树的先序序列，递归的方法去构造，将构造二叉树的任务分为构造多个子树的小任务。首先对树根结点调用构造二叉树的方法，在每一个节点处对左子树和右子树依次调用构造二叉树的方法。

我们本篇使用下面的树

这里的先序序列是一个数组，在用循环结构去构造的时候，应该使索引 i 是一个全局变量，否则每一次递归地调用create()方法的时候，i 值都会是0，最后构造出来是错误的

public class BinaryTree {

	public BinaryNode root;
	public BinaryTree(T[] prelist){
		this.root = create(prelist);
	}
	private int i = 0;
	private BinaryNode create(T[] prelist){
		BinaryNode p = null;
		if(i < prelist.length) {
			T elem = prelist[i];
			i++;
			if(elem != null) {
				p = new BinaryNode (elem);
				p.left = create(prelist);
				p.right = create(prelist);
			}
		}
		return p;
	}
}

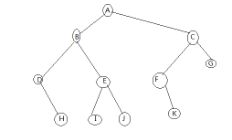
这样，构造出来了二叉树的逻辑结构。
需要注意的是，构造的时候传入的数列，应该是一个完全二叉树的形式，也就是不存在的结点也要设为null，否则这个方法错误
接下来是二叉树的非递归先序遍历方法
首先结合上面的构造体会一下效果

public static void main(String[] args) {
		//必须把所有叶子节点后面跟两个null，否则输出结果不对
		String[] prelist = {"A","B","D",null, "H",null,null,"E","I",null,null,
				"J",null,null,
				"C","F",null,"K",null,null,
				"G",null,null};
		BinaryTree bitree = new BinaryTree(prelist);
		bitree.preorderTraverse();
	}

输出结果是：
先根次序遍历 非递归
A B D ^ H ^ ^ E I ^ ^ J ^ ^ C F ^ K ^ ^ G ^

先序遍历
先根次序遍历，我们从根节点开始，设置一个指针变量指向当前节点，一直访问左子树（指针一直指向左子树），在这个过程中遇到的每一个结点都要输出它的元素值，然后入栈，直到左子树为空，我们将栈顶出栈，指针指向栈顶元素的右子树，然后仍然是入栈然后指向左子树（这里就又递归了）。依次类推…

public void preorderTraverse() {
		System.out.println("先根次序遍历 非递归");
		LinkedStack> stack = new LinkedStack>();
		BinaryNode p = this.root;
		while (p != null || !stack.isEmpty()) {
			if (p != null) {
				System.out.print(p.data + " ");
				stack.push(p);
				p = p.left;
			}else {
				System.out.print("^ ");
				p = stack.pop();
				p = p.right;
			}
		}
		System.out.println();
	}

中序遍历
然后是中序遍历，他和先序的区别也就是。先序遍历是在结点入栈的时候进行输出元素值的。而中序遍历是在元素出栈的时候输出出栈元素的元素值。怎么讲也不如体会一下代码！：

//@ author ZhaoKe
	public void inorderTraverse() {
		System.out.println("中根次序遍历 非递归");
		LinkedStack> stack = new LinkedStack>();
		BinaryNode p = this.root;
		while (p != null || !stack.isEmpty()) {
			if (p != null) {
				stack.push(p);
				p = p.left;
			}else {
				System.out.print("^ ");
				p = stack.pop();
				System.out.print(p.data + " ");
				p = p.right;
			}
		}
		System.out.println();
	}

它的输出结果是：
中根次序遍历 非递归
^ D ^ H ^ B ^ I ^ E ^ J ^ A ^ F ^ K ^ C ^ G

后序遍历
后序遍历不太一样，这里比较麻烦。由于顺着二叉树的左子树去寻找最下面的右子树的叶子结点，中间一定要有结点的入栈和出栈，那么无论是入栈还是出栈去输出结点的元素值，都是先序或中序遍历的操作，后续自然不能使用了。
因此这里我们设置一个临时存储的访问变量 last，表示刚刚是哪一个结点已经被访问过，而且刚刚访问它的时候没有输出它的值。那么这里问题是何时去输出它的值。
根据上面的例子，我们过程是：

• 仍然一直顺着左子树去到达最下面的结点， 回到上一层结点不使用出栈操作，而是“返回栈顶元素”，

• 然后去右子树，如果右子树不为空并且刚刚未访问过，就去右子树。

• 否则输出结点的值，并把该节点出栈赋值给变量 last，表示它被访问过。然后再回到上一层结点，

• 该节点再次入栈，左子树为空，去右子树，右子树被访问过，那么这个结点输出并出栈，又到了上一层结点。以此类推就完成了后序遍历

//@ author ZhaoKe
	public void postorderTraverse() {
		System.out.println("后根次序遍历 非递归");
		LinkedStack> stack = new LinkedStack>();
		BinaryNode last = null;
		BinaryNode p = this.root;
		while (p != null || !stack.isEmpty()) {
			if (p != null) {
				stack.push(p);
				p = p.left;
			}else {
				System.out.print("^ ");
				p = stack.peek();
				if(p.right != null && last != p.right) {
					p = p.right;
				}
				else {
					System.out.print(p.data+" ");
					last  =stack.pop();
//					p = stack.peek();//这是错误演示，这会导致死循环。会导致一直进入if里面而不停地入栈出栈
					p = null;
				}	
			}//else
		}//while
		System.out.println();
	}

遍历的结果是：
后根次序遍历 非递归
^ ^ H ^ D ^ ^ I ^ ^ J ^ E ^ B ^ ^ ^ K ^ F ^ ^ G ^ C ^ A