BP神经网络进行分类任务

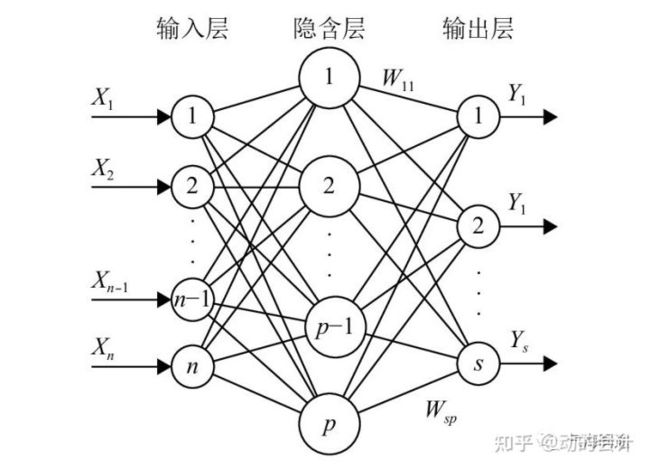
BP(Back Propagation)神经网络是一种按误差逆传播算法训练的多层前馈网络，它的学习规则是使用梯度下降法，通过反向传播来不断调整网络的权值和阈值，使网络的误差平方和最小。BP神经网络模型拓扑结构包括输入层(input)、隐层(hiddenlayer)和输出层(output layer)。BP网络的学习过程，由信息的正向传播和误差的反向传播两个过程组成。

BP神经网络示意图

下面以鸢尾花数据集为例，使用pytorch实现BP神经网络：

1 鸢尾花数据介绍Iris 鸢尾花数据集是一个经典数据集，在统计学习和机器学习领域都经常被用作示例。数据集内包含 3 类共 150 条记录，每类各 50 个数据，每条记录都有 4 项特征：花萼长度、花萼宽度、花瓣长度、花瓣宽度，通过这4个特征预测鸢尾花卉属于（iris-setosa, iris-versicolour, iris-virginica）中的哪一品种。

2 超参数设置超参数无法通过训练得到，只能经验给定，或遍历求最佳组合。

lr        = 0.02 #学习率
epochs    = 300    
n_feature = 4    # 输入特征(鸢尾花四个特征)
n_hidden  = 20   # 隐含层
n_output  = 3    # 输出(鸢尾花三种类别)

3 数据准备将数据分类训练集(80%)和测试集(20%)，训练集训练得到网络的权重，测试集评估网络的泛化误差。对数据进行归一化，测试集的数据归一化必须使用训练集上得到的最大最小值。最后将数据转化为Tensor类型，以便能够进行训练。

iris = datasets.load_iris() # 下载并导入数据
# 划分数据集和测试集
x_train0, x_test0,y_train,y_test = train_test_split(iris.data,iris.target,test_size=0.2,random_state= 22)
# 归一化
x_train = np.zeros(np.shape(x_train0))
x_test  = np.zeros(np.shape(x_test0 ))
for i in range(4):
    xMax = np.max(x_train0[:,i])
    xMin = np.min(x_train0[:,i])
    x_train[:,i] = (x_train0[:,i] - xMin)/(xMax - xMin)
    x_test[:,i]  = (x_test0[:,i]  - xMin)/(xMax - xMin)
# 数据类型转换为tensor
x_train = torch.FloatTensor(x_train)
y_train = torch.LongTensor (y_train)
x_test  = torch.FloatTensor(x_test )
y_test  = torch.LongTensor (y_test )

4 定义BP神经网络定义三层神经网络，即1输入层，1隐含层，1输出层，激活函数使用softmax。

class bpnnModel(torch.nn.Module):
def __init__(self, n_feature, n_hidden, n_output):
        super(bpnnModel, self).__init__()
        self.hidden = torch.nn.Linear(n_feature, n_hidden)   # 定义隐藏层网络
        self.out = torch.nn.Linear(n_hidden, n_output)   # 定义输出层网络
def forward(self, x):
        x = Fun.relu(self.hidden(x))        # 隐藏层的激活函数,采用relu,也可以采用sigmod,tanh
        out = Fun.softmax(self.out(x), dim=1) # 输出层softmax激活函数
return out

5 定义优化器损失函数优化器使用Adam，损失函数使用交叉熵（对于分类问题常用）。

net = bpnnModel(n_feature=n_feature, n_hidden=n_hidden, n_output=n_output)
optimizer = torch.optim.Adam(net.parameters(), lr=lr) # 优化器选用随机梯度下降方式
loss_func = torch.nn.CrossEntropyLoss() # 对于多分类一般采用的交叉熵损失函数

6 训练和测试此过程即循环epochs=300遍，每一次循环都遍历训练集的全部数据，并通过误差反向传播更新权重。

loss_steps     = np.zeros(epochs)  # 保存每一轮epoch的损失函数值
accuracy_steps = np.zeros(epochs)  # 保存每一轮epoch的在测试集上的精度
for epoch in range(epochs):
    y_pred = net(x_train)             # 前向过程
    loss = loss_func(y_pred, y_train) # 输出与label对比
    optimizer.zero_grad()             # 梯度清零
    loss.backward()                   # 反向传播
    optimizer.step()                  # 使用梯度优化器
    loss_steps[epoch] = loss.item()   # 保存loss
    # 下面计算测试机的精度，不需要求梯度
with torch.no_grad():             
        y_pred  = net(x_test) # 测试集预测
        correct = (torch.argmax(y_pred, dim=1) == y_test).type(torch.FloatTensor)
        accuracy_steps[epoch] = correct.mean()  # 测试集精度
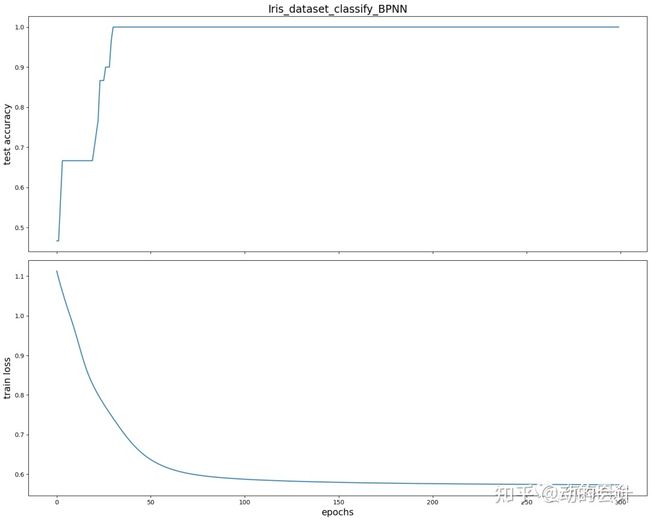
print("测试集莺尾花预测准确率",accuracy_steps[-1])

损失函数和精度曲线，训练开始，随着损失函数降低，测试集上的精度也在不断降低，但是训练在100轮以后，基本不再提升。

以下为全部代码：

import numpy as np
import matplotlib.pyplot as plt
from sklearn import datasets
from sklearn.model_selection import train_test_split #引入训练集、测试集划分函数
import torchimport torch.nn.functional as Fun

# 0. 超参数设置
lr        = 0.02
epochs    = 300
n_feature = 4
n_hidden  = 20
n_output  = 3

# 1. 数据准备
iris = datasets.load_iris()
x_train0, x_test0,y_train,y_test = train_test_split(iris.data,iris.target,test_size=0.2,random_state= 22)
x_train = np.zeros(np.shape(x_train0))
x_test  = np.zeros(np.shape(x_test0 ))
for i in range(4):    
    xMax = np.max(x_train0[:,i])    
    xMin = np.min(x_train0[:,i])    
    x_train[:,i] = (x_train0[:,i] - xMin)/(xMax - xMin)    
    x_test[:,i]  = (x_test0[:,i]  - xMin)/(xMax - xMin)
x_train = torch.FloatTensor(x_train)
y_train = torch.LongTensor(y_train)
x_test  = torch.FloatTensor(x_test )
y_test  = torch.LongTensor(y_test )

# 2. 定义BP神经网络
class bpnnModel(torch.nn.Module):    
def __init__(self, n_feature, n_hidden, n_output):        
    super(bpnnModel, self).__init__()        
    self.hidden = torch.nn.Linear(n_feature, n_hidden)  # 定义隐藏层网络        
    self.out = torch.nn.Linear(n_hidden, n_output)   # 定义输出层网络    
def forward(self, x):        
        x = Fun.relu(self.hidden(x))# 隐藏层的激活函数,采用relu,也可以采用sigmod,tanh       
        out = Fun.softmax(self.out(x), dim=1) # 输出层softmax激活函数        
return out

# 3. 定义优化器损失函数
net = bpnnModel(n_feature=n_feature, n_hidden=n_hidden, n_output=n_output)
optimizer = torch.optim.Adam(net.parameters(), lr=lr) # 优化器选用随机梯度下降方式
loss_func = torch.nn.CrossEntropyLoss() # 对于多分类一般采用的交叉熵损失函数

# 4. 训练数据
loss_steps     = np.zeros(epochs)
accuracy_steps = np.zeros(epochs)
for epoch in range(epochs):    
    y_pred = net(x_train)             # 前向过程    
    loss = loss_func(y_pred, y_train) # 输出与label对比    
    optimizer.zero_grad()             # 梯度清零    
    loss.backward()                   # 反向传播   
    optimizer.step()                  # 使用梯度优化器   
    loss_steps[epoch] = loss.item()   # 保存loss    
with torch.no_grad():        
        y_pred  = net(x_test)        
        correct = (torch.argmax(y_pred, dim=1) == y_test).type(torch.FloatTensor)        
        accuracy_steps[epoch] = correct.mean()
print("测试集莺尾花预测准确率",accuracy_steps[-1])

# 5 绘制损失函数和精度
fig_name = 'Iris_dataset_classify_BPNN'
fontsize = 15
fig, (ax1, ax2) = plt.subplots(2, figsize=(15, 12), sharex=True)
x1.plot(accuracy_steps)
ax1.set_ylabel("test accuracy", fontsize=fontsize)
ax1.set_title(fig_name, fontsize='xx-large')
ax2.plot(loss_steps)
ax2.set_ylabel("train loss", fontsize=fontsize)
ax2.set_xlabel("epochs", fontsize=fontsize)
plt.tight_layout()
plt.savefig(fig_name+'.png')
plt.show()

参考：

https://www.jianshu.com/p/52b86c774b0b

文章来源：气海同途公众号水文、生态、遥感、人工智能、大气等方向视频教程汇总https://mp.weixin.qq.com/s?__biz=MzUzMTczMDMwMw==&mid=2247500552&idx=4&sn=0d68a31fcdac77b47f1aec2c04e65f78&chksm=fabc9918cdcb100e706da62a720d2343106238ca2fc4a4aac001bad3e01d066d1355284fa6bd&token=1597410074&lang=zh_CN#rd