梯度下降法python实现

1、导数

导数表示某个瞬间的变化量。
$$\frac{df(x)}{dx}=\underset{h\to 0}{\lim }\frac{f(x+h)-f(x)}{h}$$
$\frac{df(x)}{dx}$表示f(x)关于x的导数， 即f(x)相对于x的变化程度，即，x的微小变化将导致函数f(x)产生多大程度的变化。
python 实现：

def numerical_diff(f,x):
    # 微小值h用于模拟微分计算中的趋近于0的x的变化量
    # 但h不可以设的太小，如1e-50,因为np.float32(1e-50)=0，计算机无法表示，也无法计算
    h=1e-4
    return (f(x + h) - f(x)) / h # 前向差分

# 改进的数值微分（中心差分）
def numerical_diff(f,x):
    h=1e-4
    return (f(x + h) - f(x - h)) / (2 * h) # 中心差分，比前向差分更加接近真实导数值

例子：

import numpy as np
import matplotlib.pylab as plt

def numerical_diff(f,x):
    h=1e-4 # 0.0001
    return (f(x + h) - f(x - h)) / (2 * h)

def function_1(x):
    return x**2 + x

# 画出x处的切线
def tangent_line(f,x):
    d = numerical_diff(f,x) # 斜率
    print (d)
    y = f(x) -d * x
    return lambda t: d * t + y

x = np.arange(0.0, 10.0, 0.1)
y = function_1(x)
tf = tangent_line(function_1, 5) # 返回一个lambda表达式
y2 = tf(x)
plt.xlabel("x")
plt.ylabel("f(x)")
plt.title("f(x) = x**2 + x")
plt.plot(x, y, color = "black")
plt.plot(x, y2)
plt.show()

10.999999999974364

数值微分计算结果为10.999··，和解析值11很接近。下图是x=5处的切线。

2、偏导数

偏导数和导数一样，都是某个地方的斜率。
但是，偏导数需要把多个变量中的某一个变量定位目标变量，其他变量固定值。

3、梯度

全部变量的偏导数汇总而成的向量称为梯度。 如$(\frac{\partial f}{\partial x_0},\frac{\partial f}{\partial x_1})$。
$$方向导数=梯度\times cos\theta$$
$\theta$是方向导数方向和梯度方向的夹角。
所以梯度是方向导数的最大值，所以所有的方向中，梯度方向是下降最快的方向。

梯度为0的地方，有三种可能，可能是函数的极小值，最小值和鞍点（saddle point）。
极小值，即局部最小值。
鞍点，是从某个方向看上去像是极大值，另一个方向看又像是极小值的点。
所以梯度法虽然找的是梯度为0的点，但可能实际找到了极小值或者鞍点。而且如果目标函数很复杂且呈扁平状时，学习可能会进入一个几乎平坦的地区，再也跳不出来，陷入“学习高原”，即无法前进的停滞期。
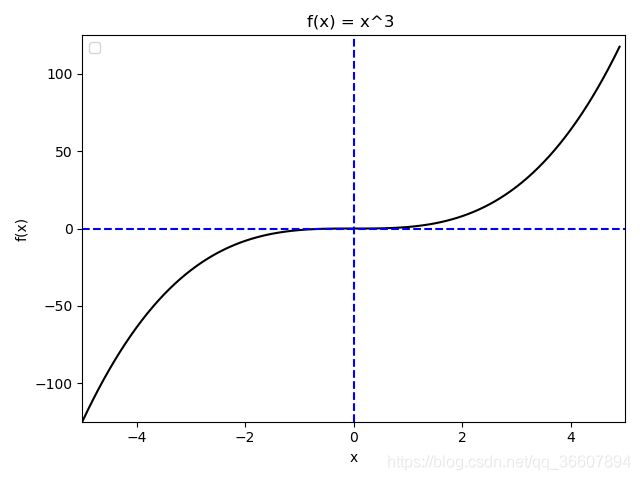
鞍点示例：$y=x^3$图像中的原点就是鞍点

import numpy as np
import matplotlib.pyplot as plt

def function(x):
    return x**3

x = np.arange(-5, 5, 0.1)
y = function(x)
plt.plot(x, y,'k')
plt.plot( [-5, 5], [0, 0], '--b')
plt.plot( [0, 0], [-125, 125], '--b')
plt.xlim(-5, 5)
plt.ylim(-125, 125)
plt.xlabel('x')
plt.ylabel('f(x)')
plt.title('f(x) = x^3 ')
plt.show()

• 计算梯度的代码模块：

# 梯度的实现，仅适用于输入x是一维向量
def numerical_gradient_1d(f, x):
    h = 1e-4
    grad = np.zeros_like(x) # 生成和x形状一样的数组，元素初始化为0

    for idx in range(x.size):
        tmp_val = x[idx]
        # 计算f(x + h)
        # 梯度是所有偏导数构成的向量，求一个变量的偏导只能让这个变量加上微小变化h
        # 其他变量不能加，所以要用for loop
        x[idx] = tmp_val + h
        fxh1 = f(x)

        # 计算f(x - h)
        x[idx] = tmp_val - h
        fxh2 = f(x)

        grad[idx] = (fxh1 - fxh2) / (2*h)
        x[idx] = tmp_val # 还原值
    return grad


print(numerical_gradient_1d(function_3, np.array([2.0, 3.0]) )) # 打印在（2,3）处计算的梯度

[4. 6.]

计算的梯度和解析计算值一样。

这段代码之前有个bug,导致算出的微分不正确，单步调试找了很久发现x[idx] = tmp_val + h这步加不上h，我还以为h太小了，导致被识别为0所以把h从0.0001改为0.001，但是还是加不上，突然想到可能是数据类型的问题，因为我代码最后一句输入的参数之前是整数！！！所以加上h后类型仍被转换为整型，就把h又舍去了······，所以果断改成浮点型，ok啦
以前不怎么重视numpy数组的数据类型，不知道到底要不要加个.0，现在明白其重要性了，python是动态类型语言，根据对象的样子判断它的类型，所以要把样子写好了。

print(numerical_gradient_1d(function_3, np.array([2, 3]) ))

上面的仅适用于输入x是一维向量的情况，不适用于输入是多维的，如权重矩阵，所以NN中不常用。

可以接受输入是矩阵的数值梯度计算函数有两种实现方法：

1. 使用enumerate()方法

def _numerical_gradient_1d(f, x):
    h = 1e-4 # 0.0001
    grad = np.zeros_like(x)
    
    for idx in range(x.size):
        tmp_val = x[idx]
        x[idx] = float(tmp_val) + h
        fxh1 = f(x) # f(x+h)
        
        x[idx] = tmp_val - h 
        fxh2 = f(x) # f(x-h)
        grad[idx] = (fxh1 - fxh2) / (2*h)
        
        x[idx] = tmp_val # 还原值
        
    return grad


def numerical_gradient_2d(f, X):
    if X.ndim == 1:
    # 如果x是一维的，则调用上面的函数
        return _numerical_gradient_1d(f, X)
    else:
        grad = np.zeros_like(X)
        
        for idx, x in enumerate(X):
            grad[idx] = _numerical_gradient_1d(f, x)
            # idx相当于X的行号索引，x则是一个个行向量
        
        return grad

2. 利用numpy的nditer对象实现多维索引

def numerical_gradient(f, x):
    h = 1e-4 # 0.0001
    grad = np.zeros_like(x)
    
    it = np.nditer(x, flags=['multi_index'], op_flags=['readwrite'])
    while not it.finished:
        idx = it.multi_index
        tmp_val = x[idx]
        x[idx] = float(tmp_val) + h
        fxh1 = f(x) # f(x+h)
        
        x[idx] = tmp_val - h 
        fxh2 = f(x) # f(x-h)
        grad[idx] = (fxh1 - fxh2) / (2*h)
        
        x[idx] = tmp_val # 还原值
        it.iternext()   
        
    return grad

• 再拿一个函数举例：
  $$f(x_1,x_2)=x_1^2+x_2^2$$
  其图像：
  

画图代码：

import numpy as np
import matplotlib.pylab as plt
from mpl_toolkits.mplot3d import Axes3D

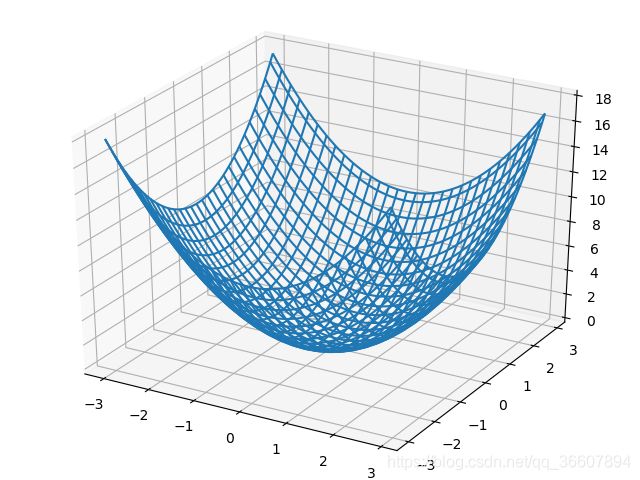
# f(x0,x1) = x0**2 + x1**2
def function_2(x,y):
    return x**2 + y**2 # np.sum(x**2)

fig = plt.figure() # 创建画布
ax = Axes3D(fig) # 创建3D图形对象
x0 = np.arange(-3, 3, 0.1)
x1 = np.arange(-3, 3, 0.1)
X, Y = np.meshgrid(x0, x1)
Z = function_2(X,Y)
ax.plot_wireframe(X,Y,Z) # 这里横纵坐标不能写x0,x1哦
plt.xlim = [-3,3]
plt.ylim = [-3,3]
plt.show()

其梯度：
画出函数$f(x,y)=x^2+y^2$在各点的梯度

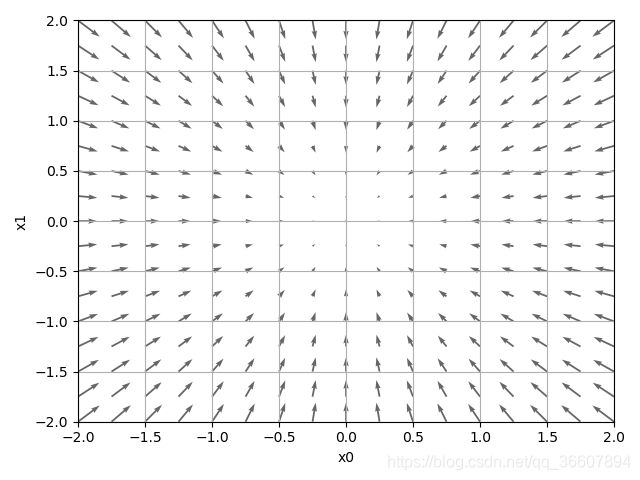
由上图可以看出，所有点的梯度都指向最低处原点(0,0),且离原点越远的梯度向量的长度越大。
但梯度并不是总指向函数的最低点，而是总指向各点处函数值降低最多的方向。（牢记！！！）
我们无法保证梯度所指的方向就是最小值或者真正应该前进的正确方向，实际上在比较复杂的函数里，梯度指向的方向一般都不是函数最小值。

图代码：

# coding: utf-8
import numpy as np
import matplotlib.pylab as plt


def _numerical_gradient_no_batch(f, x):
    h = 1e-4 # 0.0001
    grad = np.zeros_like(x)
    
    for idx in range(x.size):
        tmp_val = x[idx]
        x[idx] = float(tmp_val) + h
        fxh1 = f(x) # f(x+h)
        
        x[idx] = tmp_val - h 
        fxh2 = f(x) # f(x-h)
        grad[idx] = (fxh1 - fxh2) / (2*h)
        
        x[idx] = tmp_val # 还原值
        
    return grad


def numerical_gradient(f, X):
    if X.ndim == 1:
        return _numerical_gradient_no_batch(f, X)
    else:
        grad = np.zeros_like(X)
        
        for idx, x in enumerate(X):
            grad[idx] = _numerical_gradient_no_batch(f, x)
        
        return grad


def function_2(x):
    if x.ndim == 1:
        return np.sum(x**2)
    else:
        return np.sum(x**2, axis=1)

     
if __name__ == '__main__':
    x0 = np.arange(-2, 2.5, 0.25)
    x1 = np.arange(-2, 2.5, 0.25)
    X, Y = np.meshgrid(x0, x1)
    
    X = X.flatten()
    Y = Y.flatten()
    
    grad = numerical_gradient(function_2, np.array([X, Y]) )
    
    plt.figure()
    plt.quiver(X, Y, -grad[0], -grad[1],  angles="xy",color="#666666")
    # quiver进行箭图绘制，X,Y是箭头位置，U,V是箭头数据，angles="xy"用于绘制梯度场
    #,headwidth=10,scale=40,color="#444444")
    plt.xlim([-2, 2])
    plt.ylim([-2, 2])
    plt.xlabel('x0')
    plt.ylabel('x1')
    plt.grid()
    plt.draw()
    plt.show()

4、 梯度下降法

概念解释

Gradient descent,是一个一阶最优化算法，也叫最速下降法，用于寻找函数的极小值点，迭代搜索的方向是当前点的梯度反方向。

梯度的负方向是变量的更新方向

用于寻找函数的极大值点的方法叫做梯度上升法（gradient ascent method），本质和梯度下降一样，只是迭代搜索的方向是当前点的梯度方向。

梯度下降法，是一种数值优化方法，经常用于求解机器学习算法的模型参数，即无约束优化问题（我们知道这种问题在连续情况下，直接对所有变量求偏导，解析解就可能是极小值了不明白可以移步这篇博客），但离散问题却只能使用数值的方法一步步地迭代寻找。最小二乘法也常用于求解机器学习算法的模型参数。

梯度法使用梯度信息决定前进方向。

在梯度法中，函数的取值从当前位置沿着梯度方向前进一定距离，在新的地方重新计算梯度，再沿着新梯度方向前进，反复不断沿着梯度方向前进，从而减小函数值。
梯度法是机器学习的最优化问题中常用的方法，特别是在NN中用的更多。

数学表达

$$x_0=x_0-\eta \frac{\partial f}{\partial x_0}$$
$$x_1=x_1-\eta \frac{\partial f}{\partial x_1}$$
$$⋮$$
$$x_n=x_n-\eta \frac{\partial f}{\partial x_n}$$
$\eta$是学习率，是超参数，应该事先确定，如0.01, 0.001。
学习率过大或者过小都无法使学习过程最终抵达一个好的位置。所以一般会一边改变学习率的值，一边确认学习是否正确进行。

超参数：人工设定的参数。一般需要尝试多个值，以找到合适的参数值。如神经网络层数，每层神经元数目，学习率，CNN中滤波器尺寸等。
超参数和权重偏置参数不同，后二者是通过学习自动获得。

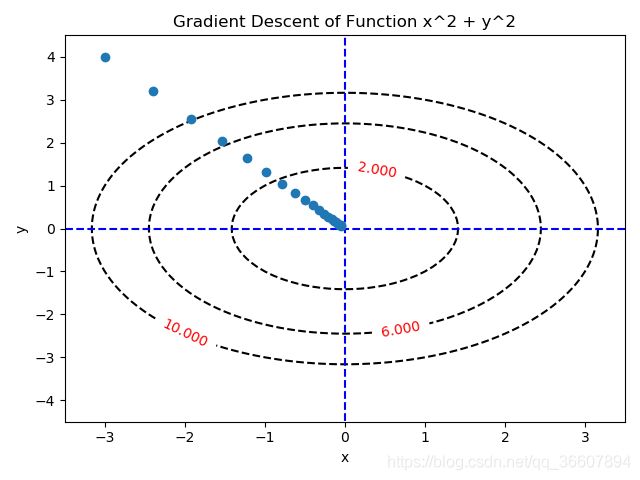
示例

下面是一个梯度下降法的例子，对函数$f(x,y)=x^2+y^2$进行梯度下降，初始值随机选了（-3,4），由梯度下降的过程图可见，成功找到了全局最小点（0,0）,且途中一直朝着全局最小走的，这是梯度下降法非常适合应用的函数类型，没有局部极小，很快（只花了20步）找到了最小点。

代码：

# coding: utf-8
import numpy as np
import matplotlib.pylab as plt


def numerical_gradient(f, X):
    if X.ndim == 1:
        return _numerical_gradient_no_batch(f, X)
    else:
        grad = np.zeros_like(X)
        
        for idx, x in enumerate(X):
            grad[idx] = _numerical_gradient_no_batch(f, x)
        
        return grad


def gradient_descent(f, init_x, lr=0.01, step_num=100):
# step_num是梯度法的重复次数
    x = init_x
    x_history = []

    for i in range(step_num):
        x_history.append( x.copy() )

        grad = numerical_gradient(f, x)
        x -= lr * grad # x根据梯度进行更新，lr:学习率

    return x, np.array(x_history)

def function_2(x):
    return x[0]**2 + x[1]**2

init_x = np.array([-3.0, 4.0])    

lr = 0.1
step_num = 20
x, x_history = gradient_descent(function_2, init_x, lr=lr, step_num=step_num)

plt.plot( [-5, 5], [0,0], '--b')
plt.plot( [0,0], [-5, 5], '--b')
plt.plot(x_history[:,0], x_history[:,1], 'o')

plt.xlim(-3.5, 3.5)
plt.ylim(-4.5, 4.5)
plt.xlabel("x")
plt.ylabel("y")
# 画函数等高线
x = np.arange(-3.3, 3.5, 0.1)
y = np.arange(-3.3, 3.5, 0.1)
X, Y = np.meshgrid(x, y)
Z = X**2 + Y**2
contour = plt.contour(X, Y, Z, [2,6,10],colors = 'k',linestyles = '--')
#[2,6,10]是只画出z=2,6,10的等高线
#等高线上标明z（高度）的值，字体大小是10，颜色红色
plt.clabel(contour,fontsize=10,colors=('r'))
plt.title('Gradient Descent of Function x^2 + y^2')
plt.show()

NN中求权重和偏置的梯度

下面是一个完整的NN中求权重和偏置的梯度的代码，仅为展示参数的梯度求解：

# 一个简单的示例NN中求解梯度的例子
# 这是一个2层网络，结构是3-2-2
# 即输入层3个神经元，隐藏层2个神经元，输出层2个unit
# 输入了两条数据，展示用BP实现高速计算梯度


import numpy as np


def sigmoid(x):
    return 1 / (1 + np.exp(-x))

def softmax(x):
    if x.ndim == 2:
        x = x.T
        x = x - np.max(x, axis=0)
        y = np.exp(x) / np.sum(np.exp(x), axis=0)
        return y.T

    x = x - np.max(x)  # 溢出对策
    return np.exp(x) / np.sum(np.exp(x))

# 计算sigmoid层的反向传播导数（根据数学推导知道是y(1-y)）
def sigmoid_grad(x):
    return (1.0 - sigmoid(x)) * sigmoid(x)


def numerical_gradient(f, x):
    h = 1e-4  # 0.0001
    grad = np.zeros_like(x)

    it = np.nditer(x, flags=['multi_index'], op_flags=['readwrite'])
    while not it.finished:
        idx = it.multi_index
        tmp_val = x[idx]
        x[idx] = float(tmp_val) + h
        fxh1 = f(x)  # f(x+h)

        x[idx] = tmp_val - h
        fxh2 = f(x)  # f(x-h)
        grad[idx] = (fxh1 - fxh2) / (2 * h)

        x[idx] = tmp_val  # 还原值
        it.iternext()

        return grad


def cross_entropy_error(y, t):
    if y.ndim == 1:
        t = t.reshape(1, t.size)
        y = y.reshape(1, y.size)

    # 监督数据是one-hot-vector的情况下，转换为正确解标签的索引
    if t.size == y.size:
        t = t.argmax(axis=1)

    batch_size = y.shape[0]
    return -np.sum(np.log(y[np.arange(batch_size), t] + 1e-7)) / batch_size


class simpleNet:
    def __init__(self, input_size, hidden_size, output_size, weight_init_std = 0.01):
        # 初始化网络
        self.params = {}
        # weight_init_std:权重初始化标准差
        self.params['W1'] = weight_init_std * \
                            np.random.randn(input_size, hidden_size) 
                            # 用高斯分布随机初始化一个权重参数矩阵
        self.params['b1'] = np.zeros(hidden_size)
        self.params['W2'] = weight_init_std * \
                            np.random.randn(hidden_size, output_size)
        self.params['b2'] = np.zeros(output_size)


    def predict(self, x):
        # 前向传播，用点乘实现
        W1, W2 = self.params['W1'], self.params['W2']
        b1, b2 = self.params['b1'], self.params['b2']

        a1 = np.dot(x, W1) + b1
        z1 = sigmoid(a1)
        a2 = np.dot(z1, W2) + b2
        y = softmax(a2)

        return y


    def loss(self, x, t):
        y = self.predict(x)
        loss = cross_entropy_error(y, t)

        return loss

    def accuracy(self, x, t):
        y = self.predict(x)
        y = np.argmax(y, axis=1)
        t = np.argmax(t, axis=1)

        accuracy = np.sum( y==t ) / float(x.shape[0])
        return accuracy

    def numerical_gradient(self, x, t):
        loss_W = lambda W: self.loss(x, t)

        grads = {}
        grads['W1'] = numerical_gradient(loss_W, self.params['W1'])
        grads['b1'] = numerical_gradient(loss_W, self.params['b1'])
        grads['W2'] = numerical_gradient(loss_W, self.params['W2'])
        grads['b2'] = numerical_gradient(loss_W, self.params['b2'])

        return grads

    # 高速版计算梯度，利用批版本的反向传播实现计算高速
    def gradient(self, x, t):
        W1, W2 = self.params['W1'], self.params['W2']
        b1, b2 = self.params['b1'], self.params['b2']
        grads = {}

        batch_num = x.shape[0]  # 把输入的所有列一起计算，因此可以快速

        # forward
        a1 = np.dot(x, W1) + b1
        z1 = sigmoid(a1)
        a2 = np.dot(z1, W2) + b2
        y = softmax(a2)

        # backward
        dy = (y - t) / batch_num  # 输出和标签的平均距离，作为损失值
        grads['W2'] = np.dot(z1.T, dy)
        # numpy数组.T就是转置
        grads['b2'] = np.sum(dy, axis=0)
        # 这里和批版本的Affine层的反向传播导数计算一样

       
        dz1 = np.dot(dy, W2.T)
        da1 = sigmoid_grad(a1) * dz1
        grads['W1'] = np.dot(x.T, da1)
        grads['b1'] = np.sum(da1, axis=0)

        return grads


net = simpleNet(input_size=3, hidden_size=2, output_size=2)
x = np.array([[0.2, 2.4, 3.9],[3.1,5.0,6.3]])  # 输入,输入两条数据
t = np.array([0, 1])  # 两个数据的标签，第一个输入的标签是0
grads = net.gradient(x, t)
print('第一层权重的梯度计算值：\n' + str(grads['W1']))
print('隐藏层偏置的梯度计算值：\n' + str(grads['b1']))
print('第二层权重的梯度计算值：\n' + str(grads['W2']))
print('输出层偏置的梯度计算值：\n' + str(grads['b2']))

输出：

第一层权重的梯度计算值：
[[-0.00517513 -0.00505167]
 [-0.01160618 -0.01133452]
 [-0.01599812 -0.01562523]]
隐藏层偏置的梯度计算值：
[-0.00313705 -0.00306456]
第二层权重的梯度计算值：
[[ 0.24212814 -0.24212814]
 [ 0.25684882 -0.25684882]]
输出层偏置的梯度计算值：
[ 0.49364622 -0.49364622]

这个程序中的高速版梯度计算一直出错，调了好久bug，实在生无可恋之余盯着报错愣了很久，突然灵光一闪，发现输入数据写错了！！！训练标签是t=[0,1]，明明是两个标签，但是输入却只写了一条！！！头铁啊！又一次陷入低端傻逼式bug···
bug版：

x = np.array([0.2, 2.4, 3.9])  
t = np.array([0, 1])  

改后版：

x = np.array([[0.2, 2.4, 3.9],[3.1,5.0,6.3]])  # 输入,输入两条数据
t = np.array([0, 1])  # 两个数据的标签，第一个输入的标签是0