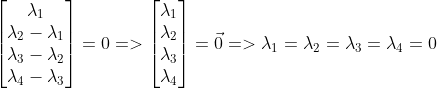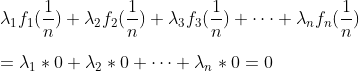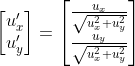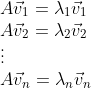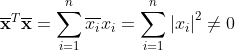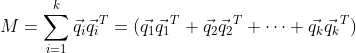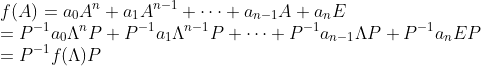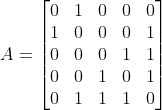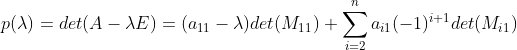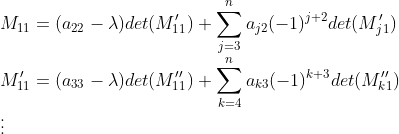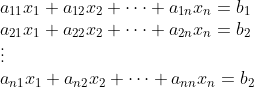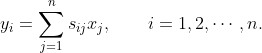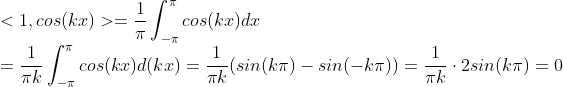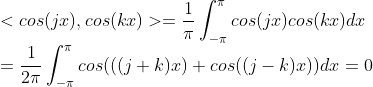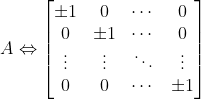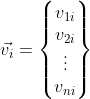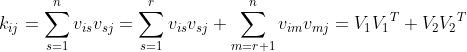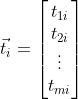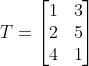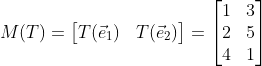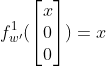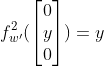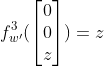线性空间一些基本性质的证明
线性代数里面蕴含着丰富的数形结合思想,结合图形来理解,难度会小很多,以下证明不一定严密,但至少不依赖任何技巧的花哨的数学方法,依赖空间直觉得出自然而然的结论,学习线性空间理论,应该低起点,高观点。
0.0结合律的证明,同济教材只给出了结论,并没有证明.
矩阵:
![]()
![]() 为一
为一![]() 矩阵,
矩阵,![]() 为一
为一![]() 矩阵,
矩阵,![]() 为一
为一![]() 矩阵,令
矩阵,令
![]()
![]()
则,需要证明![]() ,根据矩阵的乘法定义:
,根据矩阵的乘法定义:
![]()
![]() 的
的 ![]() 元为:
元为:
![]()
![]() 的
的![]() 元为:
元为:
由于
![]()
所以:
![]()
QED!
0.1![]()
![]() 为一
为一![]() 矩阵,则
矩阵,则
![]()
很普通的定理,还是要证一下:
采用数学归纳法证明对于n阶矩阵是成立的,显然,因为![]() 阶矩阵是对称的标量,结论对于
阶矩阵是对称的标量,结论对于![]() 是成立的,假设这个结论对于所有的
是成立的,假设这个结论对于所有的![]() 也是成立的,则,对于
也是成立的,则,对于 ![]() 阶矩阵A,将
阶矩阵A,将![]() 按照A的
按照A的
第一行展开,有:
![]()
![]() 为
为![]() 矩阵,由归纳假设得
矩阵,由归纳假设得
![]()
恰好是![]() 按照
按照![]() 的第一列代数余子式展开,因此
的第一列代数余子式展开,因此
![]()
QED!
1.在线性空间的理论中,有一个定理起着重要的作用,描述如下,如果向量组
![]()
中每一个向量都是向量组
的线性组合,而且m>k,则向量
![]()
必定线性相关.
证明过程如下,由题设:
必然存在KxK的满秩矩阵A,使得
![]()
是
空间向量的线性变换结果,也即是:
这样
![]()
其中
![]()
A,B互逆.
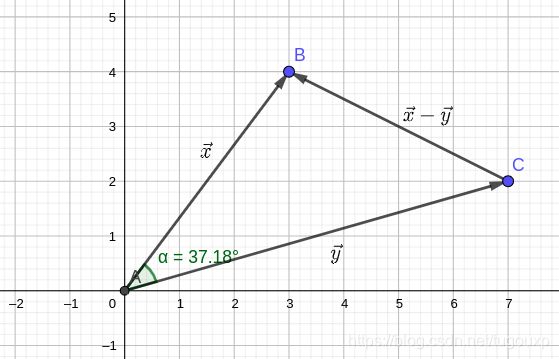
也就是说,不但x向量可以由y表示,而且也可以反过来标识y向量,两者在空间中是等价的,只是观察角度不同(玩儿游戏的同学应该能懂,吃鸡报点:))
所以,在K维空间中,哪怕在多一个向量,必定可以由k维的基标识,所以
m>k的情况下,多出来的m-k个向量必然可以被表示出来。
证毕:
对于上面证明用到的一个引理,就是为什么要求A矩阵一定满秩,简单证明如下:
反证法,先使用排中律,否定结论,设
线性无关,剩下的向量可由其表示:
![]()
所以:
则x 必然也线性相关,成功归谬,得到矛盾,引理得证明。
QED!
人类只能理解三维以下的空间,高维空间到底是什么样子的呢? 好想知道
2.关于空间中的坐标变换:
将z=4x+5y通过坐标变换变成简单形式。
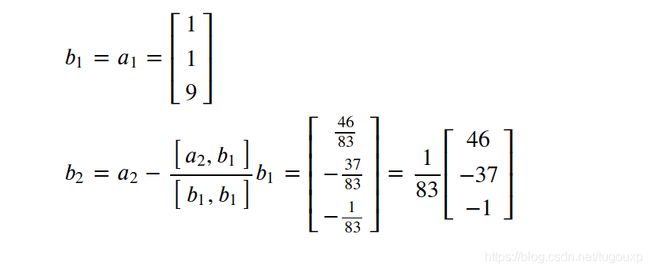
首先可以选择平面上的两个点:
比如(1,1,9)以及(2,1,13)
![]()
首先,将两个向量施密特正交化:
施密特正交化后得到:
我们主要关心方向:
![]()
将向量规范化为:
则:
所以,
![]()
去掉误差项0.0003以及0.0002后,消失了两个维度,得到简化的平面方程
空间变换是一种很重要的数据处理思想,一些看似杂乱的数据,如果换一个角度去看,在高纬度的可能存在规律的形状, 要仔细领会。
3.线性空间中有一个非常基础的论断,就是矩阵中行秩必定等于列秩,而且课本给出了证明。
看似简单,但行秩为什么必须等于列秩呢? 它究竟反应的是空间的什么结构性质呢?
对于矩阵来说,行秩=列秩,等价于说,如果行线性相关,那么列必定也线性相关,行和列不是一回事呀,包含的元素也不相同,为什么呢? 先通过一个三维空间中的例子来验证这个结论:
如下矩阵,很明显,前两行具有完全的自由度,不会线性相关,第三行由前两行线性组合而成,所以行向量必定线性相关。
![]()
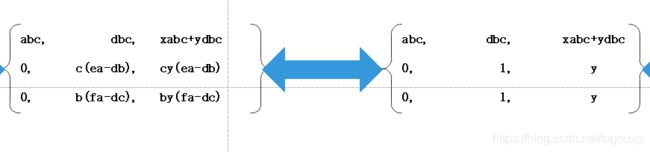
列向量是否线性相关,完全看不出任何规律,不明显,我们需要变化一下:
所以,看一看出来,转置矩阵,经过初等行变换后,最后一行简化为0,对应的原来矩阵列线性相关。
所以,原来矩阵 行线性相关<=====>矩阵列线性相关,两个等价。
上面的初等行变换过程是:
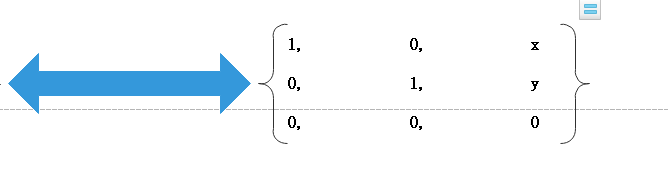
![]()
所以,行线性相关得证:
或者
![]()
让x3为自由变量:
所有由此可见,行向量线性相关必定导致有列向量标识的方程组有非零解,所有列向量也必然线性相关。
相关性和线性方程组之间的关系很微妙,如果行向量线性相关,则必定可以通过行变换消去一个方程,消去方程会导致自由变量多一个,则剩余的方程必定有非零解,有非零解同时也意味着列向量必定线性相关。。。
对于通用情况:
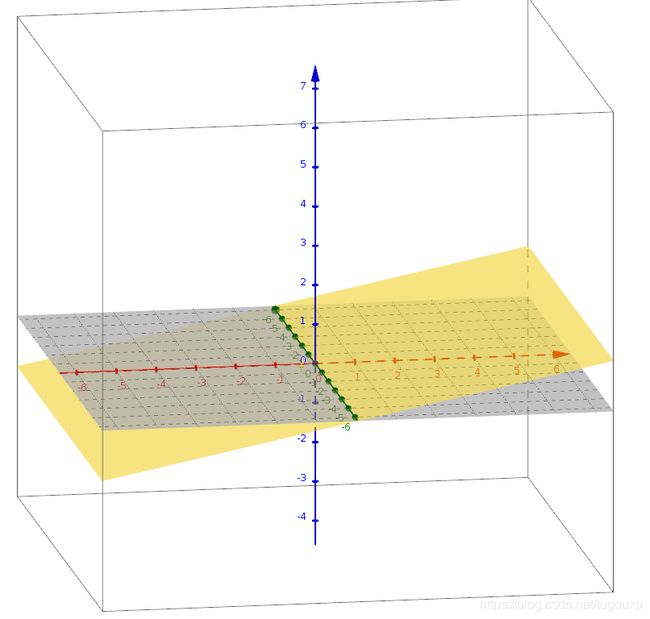
设以下mxn矩阵,其中m 将其写成列向量的格式: 假设其列秩为c,则必定存在c个列向量线性无关.我们将其挑选出来做成新的矩阵 其中 则原矩阵 线性组合的形式: 同时,也可以写成B矩阵行向量线性组合的形式: 其中 另一种证明: 考虑 考虑一下 另外,考虑到 所以 所以 QED! 初中时老师告诉我们,有n个方程才能唯一确定n个未知数,所以才叫"方“程,可是现在我们知道了,光有n个方程还不够,这些方程必须是”干货“方程才行。 4.矩阵线性组合的把戏: 以上说明,如果现行线性相关的航向量作为最后一行参与列扩张,扩张成的列向量,满足同样的行扩张系数。 5.最小二乘法的矩阵形式推导: 设: 最小二乘问题的矩阵形式: 求得向量 根据矩阵微分公式: 所以: 所以,最终得到: 对于方阵来说,它和 同解 QED! 数形结合的方法不一定到处可用,经济学中的数学模型通常有上千个变量,比如说 这样就意味着必须在 6. 1.显然 2. 所以 3. 满足标量乘法的封闭。 所以,是子空间 空间图形如下图所示: 是个过原点的二维空间。 可以想象,不过原点的二维空间是什么样子的?在这个空间中的生物,可能走一小步,就跳出了这个空间, 7:设 张成V,证明组 也张成V 满秩,所以存在逆矩阵,所以 所以,得证明! 或者 也就是 以上就是两种方法的证明! 8若将C视为R上的向量空间,则组 若将C视为C上的向量空间,则组 则 在R上,b=d=0 所以 在C上 两个方程,四个未知数,解空间是二维平面,所以有无穷多个解,例如. a=d=0, b=c=1 得到 结束! 9: 证明 假如存在 使得: 根据如下函数图形,当x取 但是 所以,显然,不存在n+1次的函数能够用<=n次的函数表达的情况,函数无关。 9:对于线性变换 所以: 所以: 所以新基下的变换为: 10:内积的定义: 对于任何 11:转置矩阵和原矩阵具有相同的特征多项式,也就是具有相同的特征值. 12:向量刻画对象,矩阵刻画对象的运动,矩阵的本质是对运动的描述,线性空间中的跃迁,交换. 运动的方式*对象=运动后的对象 12:利用范德蒙德行列式证明,属于不同特征值的特征向量线性无关: 课本上用数学归纳法,不太喜欢反证法和归纳法,还是用演绎法来证明: 假设n阶梯矩阵A有n个不同的特征值,分别为: 其对应的特征向量分别为: 证明:使得 证明过程:根据已知条件下式成立: 并且: 如果 等价于: 转化成矩阵形式: 也就是 其中: 是范德蒙德行列式,其行列式的值为: 引用特征向量各不相同的条件,则此范德蒙德行列式一定不等于0.得出此范德蒙德矩阵是满秩矩阵. 满秩矩阵就一定有唯一的逆,所以 由于 只能是 还可以认为,矩阵: 的解空间的秩为n,根据维数定理,解空间的秩+矩阵的秩=n,则矩阵的秩一定为0. 什么样的矩阵秩才为0呢?当然是0矩阵,根据上面的逻辑,同理得出, 所以属于不同特征值的特征向量线性无关. QED! 12: 因为 所以 13:实对称矩阵的特征值为实数 复数 用 从上式也可以得出,如果结论为真,那么 于是有: 和 让两式相减: 由于 所以, 所以 也就是 即,特征值为实数. 由于实对称矩阵的特征值是实数,所以,齐次线性方程组 是实系数线性方程组,又由于 得到 14:设 已知条件, 所以: 于是: 所以: 由于 15:若 的所有特征值. 标准正交,所以: 展开: 则: 根据正交条件,交叉项全部为0, 所以 也就是 所以,特征多项式为: 也就是特征值为 验证: 所以,M的每个列向量都是 同理: 所以,M-E的每个列向量都是0的特征向量。 16:对于 连边同时左乘 然后两边乘以 也就是: 所以, 特征向量不为 所以,齐次方程 有非0解,进而得到 Rank(A) 17: 正定矩阵,A是对称方阵,则,写成分块的形式: 对矩阵尽心给出等列变换,用第二列减去第一列右乘以 也就是: 根据已知矩阵正定的条件,一个矩阵是正定的,当且仅当它的各阶顺序主子式是正定的,所以 根据正定矩阵的要求, 所以 所以得到: 同理,可以得到 所以 18.若P为正交矩阵,则线性变换 称为正交变换 则 由于 19:设 题设可知: 假设 两边同时乘以 所以 由于 因为 从而 同样因为 根据 所以,线性无关结论成立. 20: 如果 则: 21:证明对称矩阵 充分性: 设矩阵 所以, 另 得到 必要性: 所以, QED! 22: 则: 代数证明卡壳了,先写到这里,后面想到在补充.下面换另一个思路证明: 对于任一初等矩阵 如果 如果B非奇异,则 23: 表示 证明:利用数学归纳法, 表示从顶点 的路的数量,另一方面,如果 所以,可以得到,从 而恰好是 24:设 证明: 按照第一列进行展开,可以得到: 将 其中 所以, 同时 对照两个式子的 另 QED! 25:cramer法则的证明: 如果: 所以 矩阵 将前式乘以伴随矩阵 也就是: 所以: 26:另 及 设 为向量 则转换成标准坐标系下表示的坐标为: 经过 所以, 所以: 所以,从 所以 所以 或者,已知 因此,若 则 于是 27:若 证明过程: 由余弦定理,我们有: 得到: QED! 28:旋转矩阵 如果 所以,对于下向量 28: 在 集合 为一个正交向量集合,因为,对任意的正整数 为了构造一个规范正交基,只要在1的方向上构造单位向量. 所以, 根据以上信息,不求原函数,计算 计算过程: 因为 分析: 29:假设在标准坐标系下的正交向量 以及 则 则加入存在新的基 则新的 所以, 当 所以, 反之,如果A并非正交变换,则结果 内积不一定为0! 同样道理,内积为0,不表示这两个向量一定正交垂直,还要看它的坐标系. 比如,二维平面连个无关向量, 大致可以得到一个结论,要准确描述向量,首先要确定一组基,然后给出在基所在的各个直线上的投影值,就可以了。为了方便求坐标,我们希望这组基向量模长为 1。因为向量的内积运算,当模长为 1 时,内积可以直接表示投影。然后还需要这组基是线性无关的,我们一般用正交基,非正交的基也是可以的,不过正交基有较好的性质。 30:正交矩阵的特征值有什么规律? 假设 特征值为 则 两边转置 同时右乘 所以, 意味着 由于实对称矩阵的特征值是实数 是实系数线性方程组,又由于 得到 这个结论有什么意义呢?从这个结论 可以得出,在三维空间中的刚体变换,一定存在一个对称轴,在对称轴方向上,刚体的尺度不发生变化。 31: 由于 且 因此,令 所以: 32:证明 因为 因为 ,所以 同样道理, 所以: 下面证明,特征值相同: 设 实际上有一个更强的结论,两个矩阵应该是相似的。 QED! 33: 其中 所以 形式上的确如此,证明一下: 设 则 34.如果当 比如,对于 其中 所以实际上 如果 但如果 例如,对于映射: 他是将二维坐标映射到三维坐标,是升维度映射,所以是单射,从下图可以看到,左边二维空间映射为右边三维空间的二维子空间,映射后的空间构成一个平面,仍然是二维的。 对偶空间: 是 则: 所以,对于 35.设A为![]()
![]()
![]() (j
(j![]()
![]()
![]()
![]()
![]()
![]() 矩阵,
矩阵,![]() 为一
为一![]() 阶矩阵,设它的行秩为
阶矩阵,设它的行秩为![]() ,列秩为
,列秩为![]() .
.![]() 的解空间,则
的解空间,则![]() 的行阶梯型
的行阶梯型![]() 将有
将有![]() 个首1元素行,必定有
个首1元素行,必定有![]() 个自由变量,所以A的解空间的维数必为
个自由变量,所以A的解空间的维数必为![]() .
.![]() 和
和![]() 是互为正交补空间,
是互为正交补空间,![]() 的秩为
的秩为![]()
![]()
![]()
![]()
![]() ,使得
,使得![]() 与
与![]() 的距离最小,翻译成数学表达就是:
的距离最小,翻译成数学表达就是:![]() ,求
,求![]() ,使得
,使得![]() 最小,2-范数表示的是向量长度,计算方法是向量各个元素的平方和再开方,求它最小值,等价于求:
最小,2-范数表示的是向量长度,计算方法是向量各个元素的平方和再开方,求它最小值,等价于求:![]() 的最小值,而:
的最小值,而:![]()
![]()
![]()
![]()
![]() 中工作,这样的空间不能通过几何手段来处理,但是代数方法却可以很好的发挥作用,因此这门学科叫做线性代数。
中工作,这样的空间不能通过几何手段来处理,但是代数方法却可以很好的发挥作用,因此这门学科叫做线性代数。![]() 是不是
是不是![]() 上的子空间.
上的子空间.![]() ,满足
,满足![]() ,所以存在加法单位元
,所以存在加法单位元![]() ,则
,则![]()
![]() ,满足加法封闭性.
,满足加法封闭性.![]() ,
, ![]()
![]()
![]()
![]()
![]()
![]() 线性无关,线性无关的一组向量可以作为
线性无关,线性无关的一组向量可以作为![]() 的一组基,所以得证!
的一组基,所以得证!![]() 是线性无关的。
是线性无关的。![]() 是线性相关的。
是线性相关的。![]()
![]()
![]()
![]()
![]() 是区间[0,1]上的连续函数。
是区间[0,1]上的连续函数。![]()
![]()
![]()
![]()
![]()
![]() 的时候
的时候![]()
![]() ,计算他在新坐标基B下的变换矩阵。
,计算他在新坐标基B下的变换矩阵。![]()
![]()
![]()
![]()
![]() ,可以将其单位化:
,可以将其单位化:![]()
![]()
![]()
![]()
![]() 成立的只能是
成立的只能是 ![]()
![]()
![]() 成立,那么下面的式一定成立:
成立,那么下面的式一定成立:![]()
![]() 作为特征向量,特征向量表示方向,不可能为0, 那么
作为特征向量,特征向量表示方向,不可能为0, 那么![]() ,得证.
,得证.![]()
![]()
![]() 与
与![]() 相似,则
相似,则 ![]() ,那么
,那么![]() 与
与![]() 有什么关系?
有什么关系?![]()
![]() 与
与![]() 相似
相似![]() 为实对称矩阵
为实对称矩阵![]() 的特征值,复向量
的特征值,复向量![]() 为对应的特征向量,即:
为对应的特征向量,即:![]()
![]() 表示
表示![]() 的共轭复数,
的共轭复数,![]() 表示
表示![]() 的共轭复向量.那么
的共轭复向量.那么![]()
![]() 也为A的特征向量.
也为A的特征向量.![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() ,所以其必有非平凡实数解,必有实的基础解系.所以,实对称矩阵不但特征值是实数,对应的特征向量也是实向量.
,所以其必有非平凡实数解,必有实的基础解系.所以,实对称矩阵不但特征值是实数,对应的特征向量也是实向量.![]() 是实对称矩阵的两个特征值,
是实对称矩阵的两个特征值,![]() 是对应的特征向量,若
是对应的特征向量,若![]() ,则
,则![]() 与
与![]() 正交.
正交.![]() ,
, ![]()
![]()
![]()
![]()
![]()
![]()
![]() ,所以只能是
,所以只能是![]() 成立,也即是
成立,也即是![]() 正交.
正交.![]() 是一组n维标准正交向量组,求矩阵
是一组n维标准正交向量组,求矩阵![]()
![]()
![]()
![]()
![]()
![]()
![]() 或者
或者![]()
![]()
![]()
![]() 的特征向量。
的特征向量。![]()
![]() 阶可逆矩阵
阶可逆矩阵![]() ,设其任意一个非零特征值
,设其任意一个非零特征值![]() ,对应的特征向量
,对应的特征向量![]() ,则
,则![]()
![]()
![]()
![]() ,得到:
,得到:![]() 是
是 ![]() 的特征值,对应特征向量不变,仍然为
的特征值,对应特征向量不变,仍然为![]() .
.![]() , 所以,对于0特征值的情况
, 所以,对于0特征值的情况![]()
![]()
![]()
![]()
![]() 为
为![]() 阶正定矩阵,则
阶正定矩阵,则![]()
![]() ,行列式不变,所以:
,行列式不变,所以:![]()
![]() 必然也是正定的。
必然也是正定的。![]()
![]()
![]()
![]()
得证!![]()
![]()
![]() 2-范数表示向量长度,所以,
2-范数表示向量长度,所以,![]() 说明经过正交变换后,线段长度保持不变,从而几何形状保持不变,这是正交变换的特性.
说明经过正交变换后,线段长度保持不变,从而几何形状保持不变,这是正交变换的特性.![]() 和
和![]() 是方阵A的两个不同特征值,
是方阵A的两个不同特征值, ![]() 和
和![]() 分别对应于
分别对应于![]() 和
和![]() 的线性无关特征向量,则
的线性无关特征向量,则 ![]()
![]() 线性无关.
线性无关.![]()
![]()
![]()
![]()
![]()
![]() 得:
得:![]()
![]()
![]() 得:
得:![]()
![]()
![]() ,所以
,所以![]()
![]() 线性无关,所以
线性无关,所以![]()
![]() 式可以化简为
式可以化简为![]()
![]() 线性无关.
线性无关.![]()
![]() 得到:
得到:![]()
![]()
![]()
![]()
![]() 为正定的充分必要条件是:存在可逆矩阵
为正定的充分必要条件是:存在可逆矩阵![]() ,使得
,使得![]() ,也就是A与单位矩阵E合同.
,也就是A与单位矩阵E合同.![]() 对称且正定,则存在正交矩阵
对称且正定,则存在正交矩阵![]() ,使得
,使得![]()
![]()
![]() 是对角矩阵
是对角矩阵![]() 对角元的平方根的对角阵,则:
对角元的平方根的对角阵,则:![]()
![]()
![]() ,由于P,C均为可逆阵,所以U必为可逆阵.
,由于P,C均为可逆阵,所以U必为可逆阵.![]()
![]()
![]() 必正定.
必正定.![]()
![]() 的
的![]() 元为:
元为:![]()
![]() 是自然数
是自然数![]() 的一个排列.
的一个排列.![]()
![]()
![]() 奇异,则
奇异,则![]()
![]()
![]() 为某图的
为某图的![]() 邻接矩阵,且
邻接矩阵,且![]()
![]() 的
的![]() 元素,则
元素,则![]() 等于顶点
等于顶点![]()
![]() 和
和![]() 间长度为
间长度为![]() 的路的条数
的路的条数![]() 时,由邻接矩阵定义得知,
时,由邻接矩阵定义得知,![]() 表示从顶点
表示从顶点![]() 到
到![]() 长度为1的路的数量,假设对某个
长度为1的路的数量,假设对某个![]() ,矩阵
,矩阵![]() 中的每一元素表示相应两顶点间长度为
中的每一元素表示相应两顶点间长度为![]() 的路的数量,因此,
的路的数量,因此,![]() 表示从顶点
表示从顶点![]() 到
到![]() 长度为
长度为![]() 的路的数量,如果有一条边
的路的数量,如果有一条边![]() ,则
,则![]()
![]() 到
到![]() 长度为
长度为![]() 的形如:
的形如:![]()
![]() 不是一条边,则从
不是一条边,则从![]() 到
到![]() 没有长度为
没有长度为![]() 的路,并且
的路,并且![]()
![]() 到
到![]() 长度为
长度为![]() 的所有路的总数为:
的所有路的总数为:![]()
![]() 的
的![]() 元素.
元素.![]() 阶矩阵
阶矩阵![]() 的特征值为
的特征值为![]() ,证明:
,证明:
![]()
![]()
![]() 为
为![]() 的特征多项式,则:
的特征多项式,则:![]() 按照同样的方式展开:
按照同样的方式展开:![]()
![]() 不包括两个对焦元素
不包括两个对焦元素![]() 和
和![]() ,更徨论其余的子式了.
,更徨论其余的子式了.![]() 的展开式式中唯一包含多于
的展开式式中唯一包含多于![]() 个对角元素的项,一定是
个对角元素的项,一定是![]()
![]()
![]() 系数,得到
系数,得到![]()
![]() ,根据跟与系数的关系,可得:
,根据跟与系数的关系,可得:![]()
![]()
![]()
![]()
![]() 的伴随矩阵为:
的伴随矩阵为:![]()
![]()
![]() 为一个向量空间
为一个向量空间![]()
![]() 的两个有序基,并令
的两个有序基,并令![]()
![]() 为
为![]() 上的线性算子,令
上的线性算子,令![]() 为从
为从![]() 到
到![]() 的转移表示矩阵.
的转移表示矩阵.![]() 在
在![]() 世界中的坐标
世界中的坐标![]() 变换后,坐标变为:
变换后,坐标变为:![]()
![]() 是
是![]() 世界的坐标,变为标准坐标系:
世界的坐标,变为标准坐标系:![]()
![]() 世界的角度看
世界的角度看![]() ,
, ![]() 的坐标分别为
的坐标分别为![]()
![]() 是从E到F的转移矩阵.
是从E到F的转移矩阵.![]() ,
,![]()
![]() 和
和![]() 为
为![]() 或者
或者![]() 中的两个非零向量,且
中的两个非零向量,且![]() 为它们之间的夹角,则:
为它们之间的夹角,则:![]()
![]()
![]()
![]() ,则
,则![]()
![]() ,经过正交变换后,长度不变
,经过正交变换后,长度不变![]()
![]() 上定义内积,
上定义内积,![]() ,
,![]()
![]() 和
和![]()
![]() 是单位向量,因为:
是单位向量,因为:![]()
![]()
![]()
![]() ,从
,从![]() 到标准坐标系的转移矩阵是
到标准坐标系的转移矩阵是![]()
![]() 的内积是?
的内积是?![]()
![]()
![]() 为正交变换时,
为正交变换时,![]()
![]()
![]()
![]() ,其中
,其中![]() ,则以他们为基的坐标点
,则以他们为基的坐标点![]() 和
和![]() 虽然内积为0,但他们并不垂直.
虽然内积为0,但他们并不垂直.
![]() 是正交矩阵,则
是正交矩阵,则![]()
![]() ,对应特征向量
,对应特征向量![]()
![]()
![]()
![]()
![]() 阶正交矩阵一定相似于
阶正交矩阵一定相似于![]()
![]() ,不失一般性,假设是1,所以,齐次线性方程组
,不失一般性,假设是1,所以,齐次线性方程组![]()
![]()
![]() , 所以其必有非平凡实数解,也就是必有实的基础解系.正交矩阵不但有着实的特征值,其特征向量也是实的。
, 所以其必有非平凡实数解,也就是必有实的基础解系.正交矩阵不但有着实的特征值,其特征向量也是实的。![]() 为一
为一![]() 实矩阵,它有一个复特征值
实矩阵,它有一个复特征值![]() ,并令
,并令![]() 为属于
为属于![]() 的一个特征向量,向量
的一个特征向量,向量![]() 可以分解为实部和虚部.
可以分解为实部和虚部.![]() 的元素均为实的,可得
的元素均为实的,可得![]() 也是
也是![]() 的一个特征值,它相应的特征向量为:
的一个特征值,它相应的特征向量为:![]() 和
和![]() 均为一阶方程组
均为一阶方程组![]() 的解,这两个解的任意线性组合也将是一个解,
的解,这两个解的任意线性组合也将是一个解,![]()
![]() 和
和![]() 具有相同的非零特征值
具有相同的非零特征值 ![]() 是一个
是一个![]() 的矩阵
的矩阵![]() ,所以
,所以![]() 的解同样为
的解同样为![]() 的解。
的解。![]()
![]() 的解同样也是
的解同样也是![]() 的解,所以在
的解,所以在![]() 空间中,它们具有相同的零空间,所以
空间中,它们具有相同的零空间,所以![]()
![]()
![]()
![]() 是
是![]() 的特征值
的特征值![]() 对应的特征向量
对应的特征向量![]()
![]()
![]()
![]() 中的元素
中的元素![]()
![]() ,必有
,必有![]() ,则
,则![]() 是单的,也叫“一对一”的映射。
是单的,也叫“一对一”的映射。![]()
![]() 是一个
是一个![]() 的矩阵,而
的矩阵,而![]() 是单的等价于方程组
是单的等价于方程组![]() 有唯一解.
有唯一解.![]() ,则表示方程数目大于未知量的数目,相当于从低维空间映射到高维空间,则在系数无关的情况下必定有唯一解或者无解,所以,可能是单的。
,则表示方程数目大于未知量的数目,相当于从低维空间映射到高维空间,则在系数无关的情况下必定有唯一解或者无解,所以,可能是单的。![]() ,则表示方程数目小于未知量数目,相当于从高维空间映射到低维空间,必然有多个非零解,所以,不可能是单的。
,则表示方程数目小于未知量数目,相当于从高维空间映射到低维空间,必然有多个非零解,所以,不可能是单的。
![]() 的线性映射,
的线性映射,![]() 是
是![]() 空间,
空间,![]() 是
是![]() 空间。
空间。![]() 的基是
的基是 ![]() 的基是
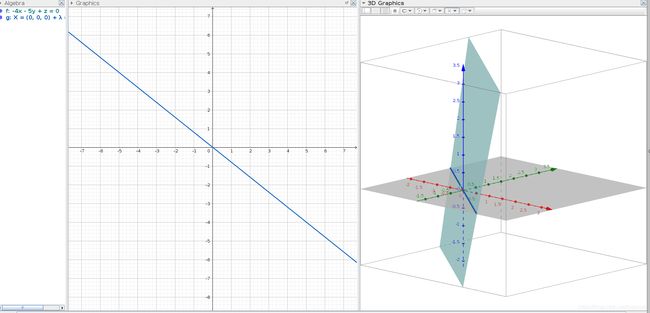
的基是 ![]() 的映射
的映射![]()
![]() 阶对称矩阵,
阶对称矩阵,![]() 是A的特征方程的r重根,则矩阵
是A的特征方程的r重根,则矩阵![]() 的秩
的秩![]() ,从而对应特征值
,从而对应特征值![]() 恰好有r线性无关的特征向量.
恰好有r线性无关的特征向量.结束!
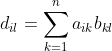
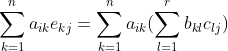
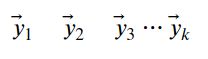
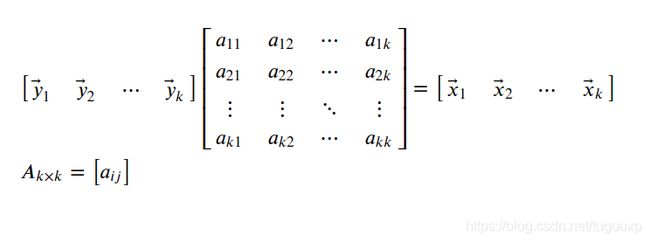
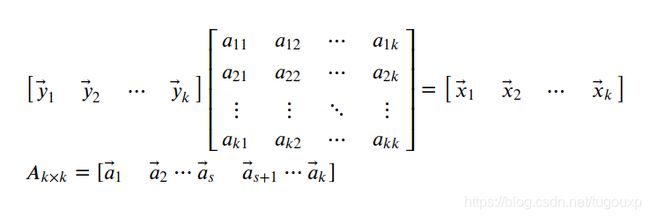
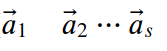
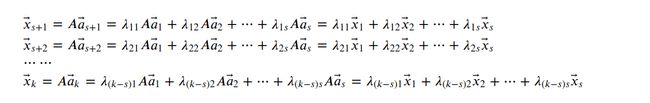
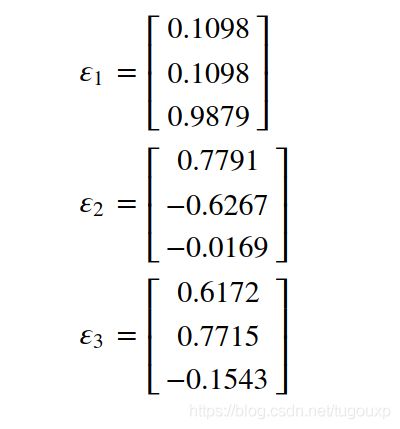




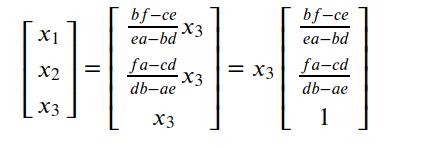
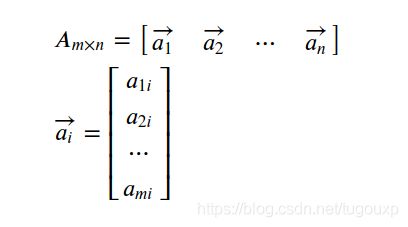
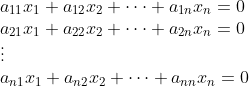
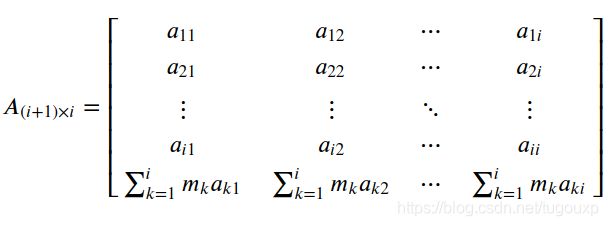
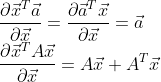
![[v_1-v_2, v_2-v_3, v_3-v_4, v_4]=[v_1, v_2,v_3, v_4]\begin{bmatrix} 1 & 0 & 0 & 0\\ -1& 1 & 0& 0\\ 0 & -1& 1& 0\\ 0 & 0 & -1& 1 \end{bmatrix}](http://img.e-com-net.com/image/info8/13f2267d61724abebac1894b8ab0cce6.gif)
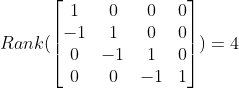
![[v_1, v_2,v_3, v_4]=[v_1-v_2, v_2-v_3, v_3-v_4, v_4]\begin{bmatrix} 1 & 0 & 0 & 0\\ -1& 1 & 0& 0\\ 0 & -1& 1& 0\\ 0 & 0 & -1& 1 \end{bmatrix}^{-1}](http://img.e-com-net.com/image/info8/80d350f95a724e2bbb5e2084c5f6d002.gif)